 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 „Eingehende Analyse': Erkundung des LiDAR-Punktwolken-Segmentierungsalgorithmus beim autonomen Fahren
„Eingehende Analyse': Erkundung des LiDAR-Punktwolken-Segmentierungsalgorithmus beim autonomen Fahren
„Eingehende Analyse': Erkundung des LiDAR-Punktwolken-Segmentierungsalgorithmus beim autonomen Fahren
Zu den derzeit gängigen Algorithmen zur Segmentierung von Laserpunktwolken gehören Methoden, die auf der Ebenenanpassung basieren, und Methoden, die auf den Eigenschaften von Laserpunktwolkendaten basieren. Die Details sind wie folgt:
Punktwolken-Bodensegmentierungsalgorithmus
01 Methode basierend auf Ebenenanpassung – Bodenebenenanpassung
Algorithmusidee: Eine einfache Verarbeitungsmethode ist entlang der x-Richtung (Die Richtung der Vorderseite des Autos) unterteilt den Raum in mehrere Unterebenen und verwendet dann den Ground-Plane-Fitting-Algorithmus (GPF) für jede Unterebene, um eine Bodensegmentierungsmethode zu erhalten, die steile Hänge bewältigen kann. Diese Methode dient dazu, eine globale Ebene in eine einzelne Punktwolke einzupassen. Sie funktioniert besser, wenn die Anzahl der Punktwolken spärlich ist, kann es leicht zu Fehlerkennungen und falschen Erkennungen kommen, z. B. bei 16 Linien Lidar.
Algorithmus-Pseudocode:

Pseudocode
Der Algorithmusprozess besteht darin, dass für eine gegebene Punktwolke P das Endergebnis der Segmentierung zwei Punktwolkensätze sind, Bodenpunktwolke und Nicht-Punktwolke. Bodenpunktwolke Punktwolke. Dieser Algorithmus verfügt über vier wichtige Parameter:
- Niter: Die Häufigkeit, mit der die Singulärwertzerlegung (SVD) durchgeführt wird, d. h. die Anzahl der Optimierungsanpassungen.
- NLPR: Wird zur Auswahl der niedrigsten Höhe verwendet Punkt der LPR-Menge
- Thseed: Schwellenwert für die Auswahl von Startpunkten. Wenn die Höhe eines Punkts in der Punktwolke kleiner als die Höhe von LPR plus diesem Schwellenwert ist, fügen wir den Punkt zum Startpunktsatz hinzu
- Thdist: Ebenenabstandsschwellenwert. Wir berechnen den Abstand von jedem Punkt in der Punktwolke zur orthogonalen Projektion der Ebene, die wir anpassen, und dieser Ebenenabstandsschwellenwert wird verwendet, um zu bestimmen, ob der Punkt zum Boden gehört
Auswahl des Startpunktsatzes
Wir wählen zunächst einen Startpunktsatz (Startpunktsatz) aus. Diese Startpunktsätze werden aus Punkten mit kleineren Höhen (d. h. Z-Werten) in der Punktwolke abgeleitet anfängliches ebenes Modell, das den Boden beschreibt. Wie wählt man also aus? Was ist mit dieser Samensammlung? Wir stellen das Konzept des Lowest Point Representative (LPR) vor. LPR ist der Durchschnitt der niedrigsten Höhenpunkte von NLPR. LPR stellt sicher, dass die Ebenenanpassungsphase nicht durch Messrauschen beeinträchtigt wird.

Auswahl der Startpunkte
Die Eingabe ist ein Rahmen der Punktwolke, der entlang der Z-Richtung (d. h. der Höhe) sortiert wurde Ermitteln Sie die durchschnittliche Höhe lpr_height (dh LPR) und wählen Sie den Punkt mit einer Höhe kleiner als lpr_height + th_seeds_ als Startpunkt aus.
Die spezifische Code-Implementierung ist wie folgt
/*
@brief Extract initial seeds of the given pointcloud sorted segment.
This function filter ground seeds points accoring to heigt.
This function will set the `g_ground_pc` to `g_seed_pc`.
@param p_sorted: sorted pointcloud
@param ::num_lpr_: num of LPR points
@param ::th_seeds_: threshold distance of seeds
@param ::
*/
void PlaneGroundFilter::extract_initial_seeds_(const pcl::PointCloud &p_sorted)
{
// LPR is the mean of low point representative
double sum = 0;
int cnt = 0;
// Calculate the mean height value.
for (int i = 0; i Flugzeugmodell
Als nächstes erstellen wir ein Ebenenmodell. Wenn der orthogonale Projektionsabstand eines Punktes in der Punktwolke zu dieser Ebene kleiner ist als der Schwellenwert Thdist, dann wird der Punkt berücksichtigt Es gehört zum Boden, andernfalls gehört es zum Nichtboden. Für die Schätzung des Ebenenmodells wird ein einfaches lineares Modell wie folgt verwendet: von Die Kovarianzmatrix C des Anfangspunktsatzes wird zur Lösung von n verwendet, um eine Ebene zu bestimmen. Der Startpunktsatz wird als Anfangspunktsatz verwendet und seine Kovarianzmatrix ist
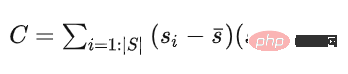
这个协方差矩阵 C 描述了种子点集的散布情况,其三个奇异向量可以通过奇异值分解(SVD)求得,这三个奇异向量描述了点集在三个主要方向的散布情况。由于是平面模型,垂直于平面的法向量 n 表示具有最小方差的方向,可以通过计算具有最小奇异值的奇异向量来求得。
那么在求得了 n 以后, d 可以通过代入种子点集的平均值 ,s(它代表属于地面的点) 直接求得。整个平面模型计算代码如下:
/*
@brief The function to estimate plane model. The
model parameter `normal_` and `d_`, and `th_dist_d_`
is set here.
The main step is performed SVD(UAV) on covariance matrix.
Taking the sigular vector in U matrix according to the smallest
sigular value in A, as the `normal_`. `d_` is then calculated
according to mean ground points.
@param g_ground_pc:global ground pointcloud ptr.
*/
void PlaneGroundFilter::estimate_plane_(void)
{
// Create covarian matrix in single pass.
// TODO: compare the efficiency.
Eigen::Matrix3f cov;
Eigen::Vector4f pc_mean;
pcl::computeMeanAndCovarianceMatrix(*g_ground_pc, cov, pc_mean);
// Singular Value Decomposition: SVD
JacobiSVD svd(cov, Eigen::DecompositionOptions::ComputeFullU);
// use the least singular vector as normal
normal_ = (svd.matrixU().col(2));
// mean ground seeds value
Eigen::Vector3f seeds_mean = pc_mean.head();
// according to normal.T*[x,y,z] = -d
d_ = -(normal_.transpose() * seeds_mean)(0, 0);
// set distance threhold to `th_dist - d`
th_dist_d_ = th_dist_ - d_;
// return the equation parameters
}优化平面主循环
extract_initial_seeds_(laserCloudIn);
g_ground_pc = g_seeds_pc;
// Ground plane fitter mainloop
for (int i = 0; i clear();
g_not_ground_pc->clear();
//pointcloud to matrix
MatrixXf points(laserCloudIn_org.points.size(), 3);
int j = 0;
for (auto p : laserCloudIn_org.points)
{
points.row(j++) points.push_back(laserCloudIn_org[r]);
}
}
}得到这个初始的平面模型以后,我们会计算点云中每一个点到该平面的正交投影的距离,即 points * normal_,并且将这个距离与设定的阈值(即th_dist_d_) 比较,当高度差小于此阈值,我们认为该点属于地面,当高度差大于此阈值,则为非地面点。经过分类以后的所有地面点被当作下一次迭代的种子点集,迭代优化。
02 基于雷达数据本身特点的方法-Ray Ground Filter
代码
https://www.php.cn/link/a8d3b1e36a14da038a06f675d1693dd8
算法思想
Ray Ground Filter算法的核心是以射线(Ray)的形式来组织点云。将点云的 (x, y, z)三维空间降到(x,y)平面来看,计算每一个点到车辆x正方向的平面夹角 θ, 对360度进行微分,分成若干等份,每一份的角度为0.2度。
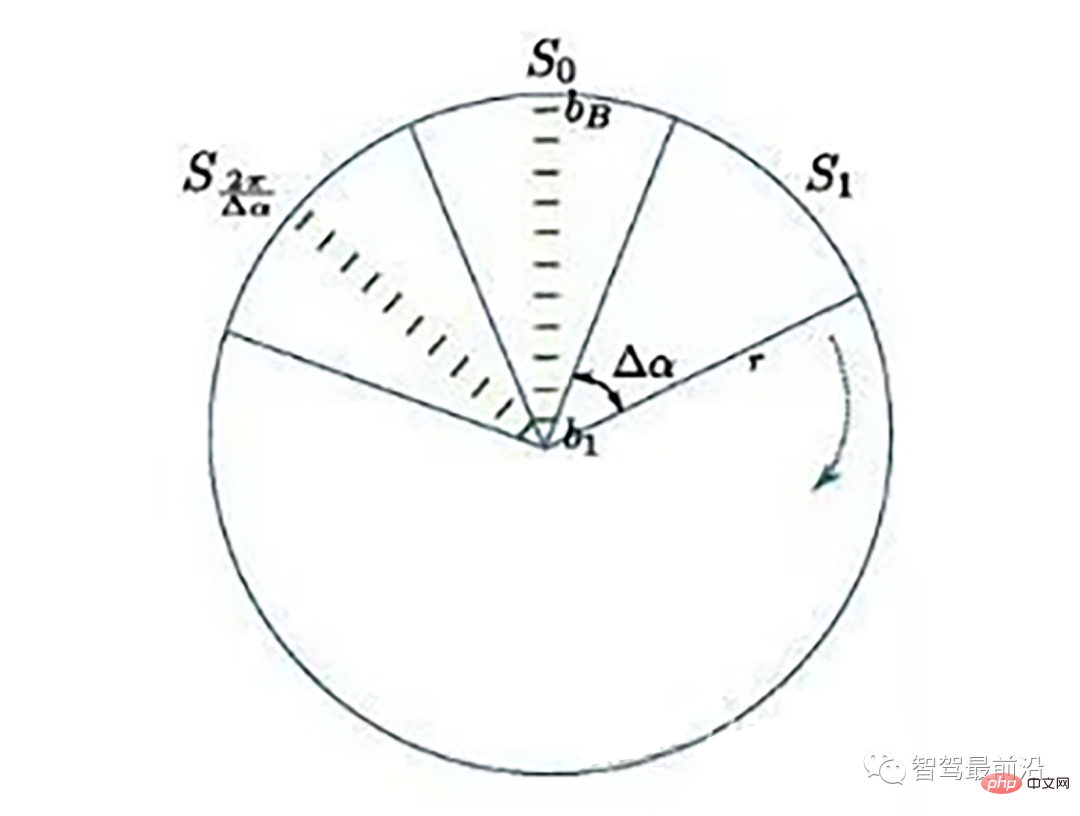
激光线束等间隔划分示意图(通常以激光雷达角度分辨率划分)
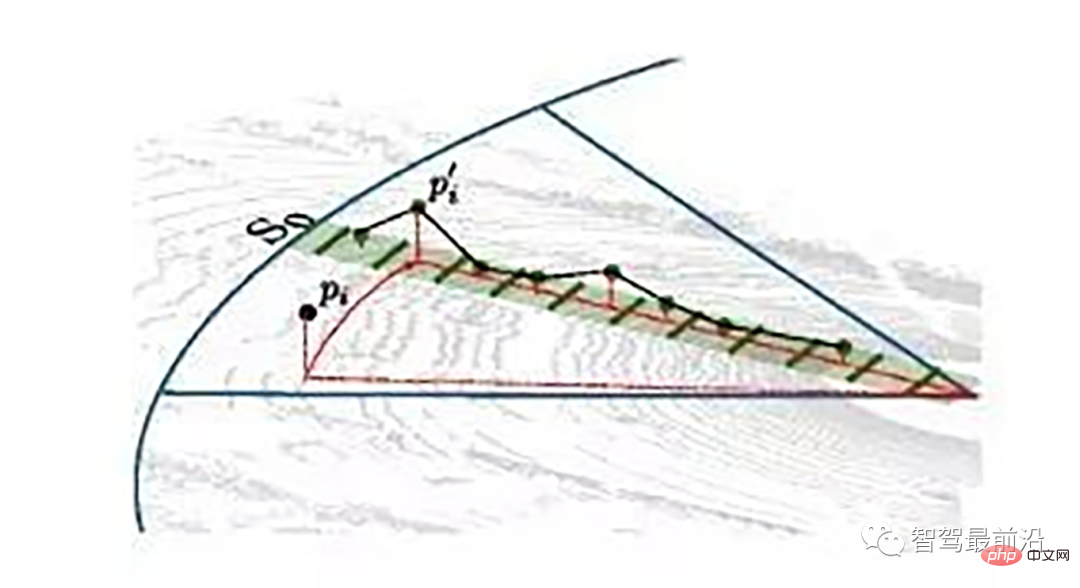
同一角度范围内激光线束在水平面的投影以及在Z轴方向的高度折线示意图
为了方便对同一角度的线束进行处理,要将原来直角坐标系的点云转换成柱坐标描述的点云数据结构。对同一夹角的线束上的点按照半径的大小进行排序,通过前后两点的坡度是否大于我们事先设定的坡度阈值,从而判断点是否为地面点。
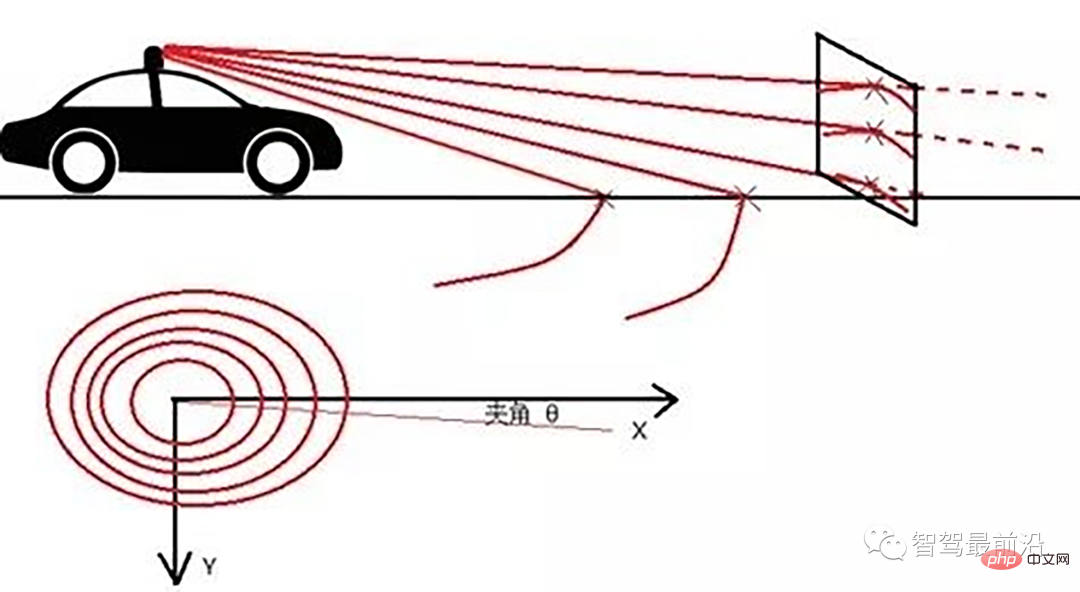
线激光线束纵截面与俯视示意图(n=4)
通过如下公式转换成柱坐标的形式:
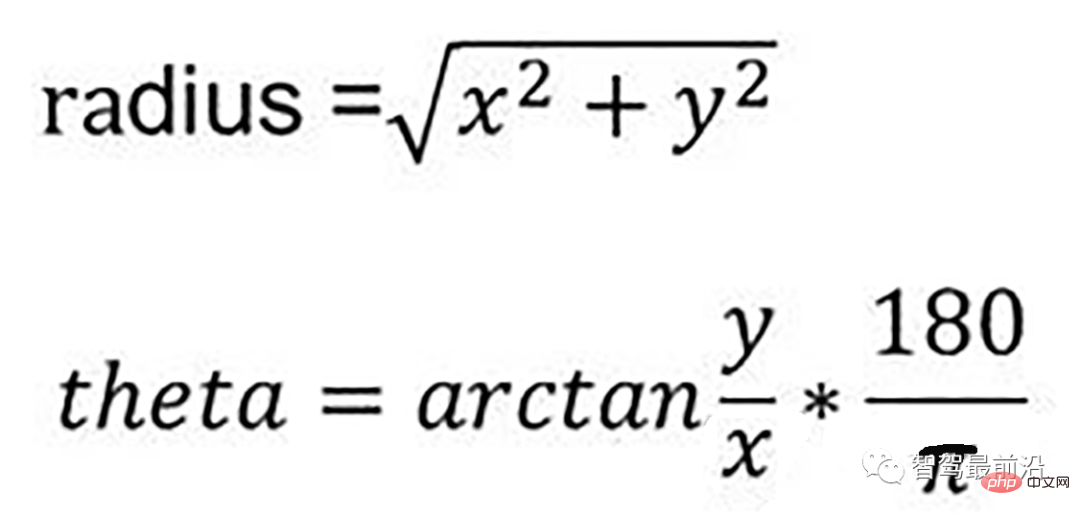
转换成柱坐标的公式
radius表示点到lidar的水平距离(半径),theta是点相对于车头正方向(即x方向)的夹角。对点云进行水平角度微分之后,可得到1800条射线,将这些射线中的点按照距离的远近进行排序。通过两个坡度阈值以及当前点的半径求得高度阈值,通过判断当前点的高度(即点的z值)是否在地面加减高度阈值范围内来判断当前点是为地面。
伪代码

伪代码
- local_max_slope_ :设定的同条射线上邻近两点的坡度阈值。
- general_max_slope_ :整个地面的坡度阈值
遍历1800条射线,对于每一条射线进行如下操作:
1.计算当前点和上一个点的水平距离pointdistance
2.根据local_max_slope_和pointdistance计算当前的坡度差阈值height_threshold
3.根据general_max_slope_和当前点的水平距离计算整个地面的高度差阈值general_height_threshold
4.若当前点的z坐标小于前一个点的z坐标加height_threshold并大于前一个点的z坐标减去height_threshold:
5.若当前点z坐标小于雷达安装高度减去general_height_threshold并且大于相加,认为是地面点
6.否则:是非地面点。
7.若pointdistance满足阈值并且前点的z坐标小于雷达安装高度减去height_threshold并大于雷达安装高度加上height_threshold,认为是地面点。
/*!
*
* @param[in] in_cloud Input Point Cloud to be organized in radial segments
* @param[out] out_organized_points Custom Point Cloud filled with XYZRTZColor data
* @param[out] out_radial_divided_indices Indices of the points in the original cloud for each radial segment
* @param[out] out_radial_ordered_clouds Vector of Points Clouds, each element will contain the points ordered
*/
void PclTestCore::XYZI_to_RTZColor(const pcl::PointCloud::Ptr in_cloud,
PointCloudXYZIRTColor &out_organized_points,
std::vector &out_radial_divided_indices,
std::vector &out_radial_ordered_clouds)
{
out_organized_points.resize(in_cloud->points.size());
out_radial_divided_indices.clear();
out_radial_divided_indices.resize(radial_dividers_num_);
out_radial_ordered_clouds.resize(radial_dividers_num_);
for (size_t i = 0; i points.size(); i++)
{
PointXYZIRTColor new_point;
//计算radius和theta
//方便转到柱坐标下。
auto radius = (float)sqrt(
in_cloud->points[i].x * in_cloud->points[i].x + in_cloud->points[i].y * in_cloud->points[i].y);
auto theta = (float)atan2(in_cloud->points[i].y, in_cloud->points[i].x) * 180 / M_PI;
if (theta points[i];
new_point.radius = radius;
new_point.theta = theta;
new_point.radial_div = radial_div;
new_point.concentric_div = concentric_div;
new_point.original_index = i;
out_organized_points[i] = new_point;
//radial divisions更加角度的微分组织射线
out_radial_divided_indices[radial_div].indices.push_back(i);
out_radial_ordered_clouds[radial_div].push_back(new_point);
} //end for
//将同一根射线上的点按照半径(距离)排序
#pragma omp for
for (size_t i = 0; i 03 基于雷达数据本身特点的方法-urban road filter
原文
Real-Time LIDAR-Based Urban Road and Sidewalk Detection for Autonomous Vehicles
代码
https://www.php.cn/link/305fa4e2c0e76dd586553d64c975a626
z_zero_method
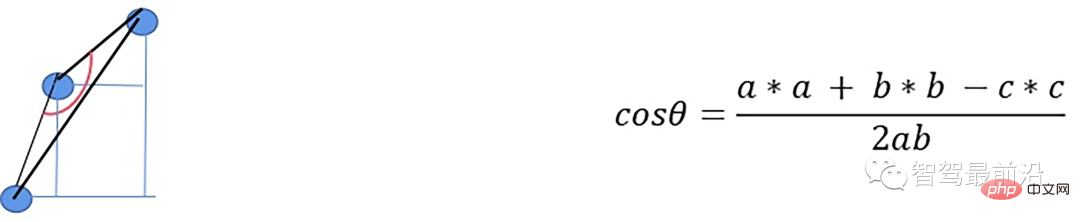
z_zero_method
首先将数据组织成[channels][thetas]
对于每一条线,对角度进行排序
- 以当前点p为中心,向左选k个点,向右选k个点
- 分别计算左边及右边k个点与当前点在x和y方向差值的均值
- 同时计算左边及右边k个点的最大z值max1及max2
- 根据余弦定理求解余弦角
如果余弦角度满足阈值且max1减去p.z满足阈值或max2减去p.z满足阈值且max2-max1满足阈值,认为此点为障碍物,否则就认为是地面点。
x_zero_method
X-zero和Z-zero方法可以找到避开测量的X和Z分量的人行道,X-zero和Z-zero方法都考虑了体素的通道数,因此激光雷达必须与路面平面不平行,这是上述两种算法以及整个城市道路滤波方法的已知局限性。X-zero方法去除了X方向的值,使用柱坐标代替。
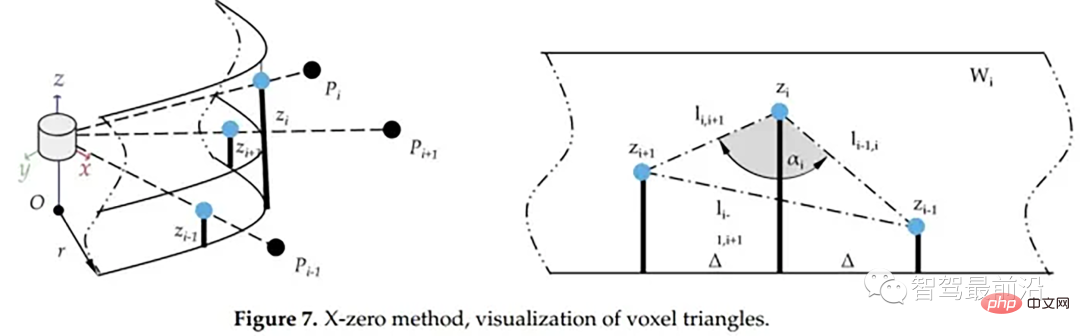
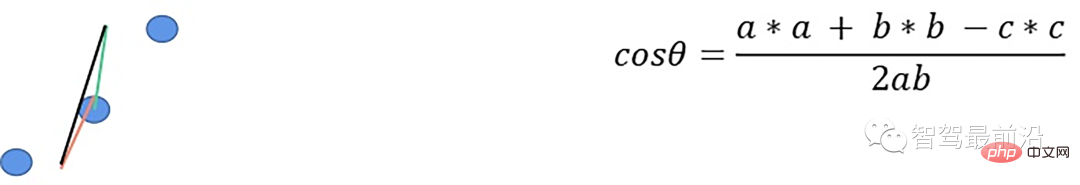
x_zero_method
首先将数据组织成[channels][thetas]
Sortieren Sie für jede Linie die Winkel
- Wählen Sie mit dem aktuellen Punkt p als Mittelpunkt den k/2-ten Punkt p1 und den k-ten Punkt p2 rechts aus
- Berechnen Sie p und p1 bzw. p1 und p2. der Abstand zwischen p und p2 in z-Richtung
- Lösen Sie den Kosinuswinkel gemäß dem Kosinussatz
Wenn der Kosinuswinkel den Schwellenwert erreicht und p1.z-p.z den Schwellenwert oder p1.z-p2 erreicht .z erfüllt den Schwellenwert und p.z- p2.z erfüllt den Schwellenwert und betrachtet diesen Punkt als Hindernis
star_search_method
Diese Methode unterteilt die Punktwolke in rechteckige Segmente, und die Kombination dieser Formen ähnelt einem Stern ; daher der Name, da der erstellte Algorithmus aus jedem Straßensegment mögliche Startpunkte für den Bürgersteig extrahiert und auf Höhenänderungen basierend auf der Z-Koordinate unempfindlich ist, was bedeutet, dass der Algorithmus in der Praxis auch dann gut funktioniert, wenn der Lidar relativ geneigt ist zur Straßenebene, in einem zylindrischen Koordinatensystem Prozesspunktwolken.
Spezifische Implementierung:
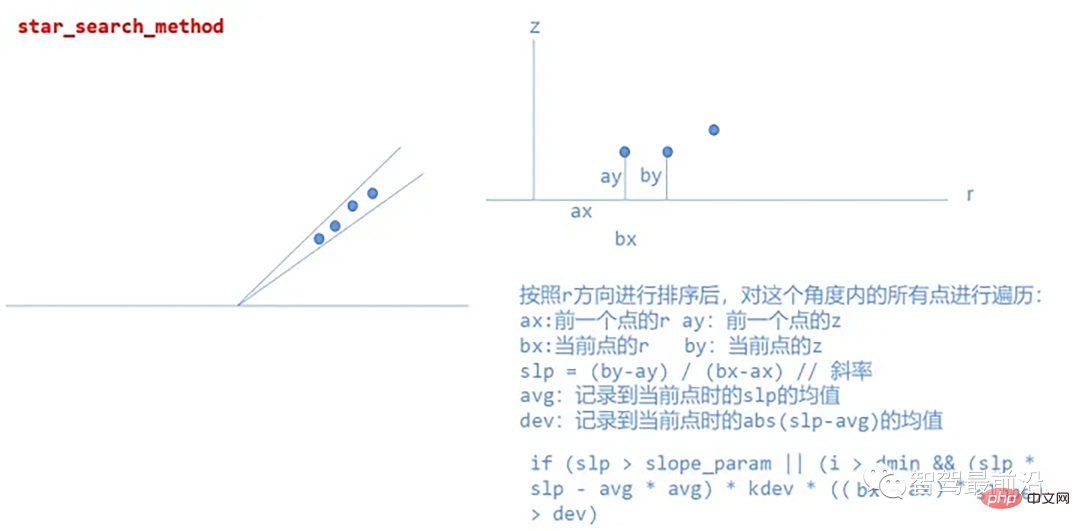
star_search_method
Das obige ist der detaillierte Inhalt von„Eingehende Analyse': Erkundung des LiDAR-Punktwolken-Segmentierungsalgorithmus beim autonomen Fahren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Oben geschrieben und persönliches Verständnis des Autors. Dreidimensionales Gaussplatting (3DGS) ist eine transformative Technologie, die in den letzten Jahren in den Bereichen explizite Strahlungsfelder und Computergrafik entstanden ist. Diese innovative Methode zeichnet sich durch die Verwendung von Millionen von 3D-Gaußkurven aus, was sich stark von der Neural Radiation Field (NeRF)-Methode unterscheidet, die hauptsächlich ein implizites koordinatenbasiertes Modell verwendet, um räumliche Koordinaten auf Pixelwerte abzubilden. Mit seiner expliziten Szenendarstellung und differenzierbaren Rendering-Algorithmen garantiert 3DGS nicht nur Echtzeit-Rendering-Fähigkeiten, sondern führt auch ein beispielloses Maß an Kontrolle und Szenenbearbeitung ein. Dies positioniert 3DGS als potenziellen Game-Changer für die 3D-Rekonstruktion und -Darstellung der nächsten Generation. Zu diesem Zweck geben wir erstmals einen systematischen Überblick über die neuesten Entwicklungen und Anliegen im Bereich 3DGS.
 Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Gestern wurde ich während des Interviews gefragt, ob ich irgendwelche Long-Tail-Fragen gestellt hätte, also dachte ich, ich würde eine kurze Zusammenfassung geben. Das Long-Tail-Problem des autonomen Fahrens bezieht sich auf Randfälle bei autonomen Fahrzeugen, also mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. Das wahrgenommene Long-Tail-Problem ist einer der Hauptgründe, die derzeit den betrieblichen Designbereich intelligenter autonomer Einzelfahrzeugfahrzeuge einschränken. Die zugrunde liegende Architektur und die meisten technischen Probleme des autonomen Fahrens wurden gelöst, und die verbleibenden 5 % der Long-Tail-Probleme wurden nach und nach zum Schlüssel zur Einschränkung der Entwicklung des autonomen Fahrens. Zu diesen Problemen gehören eine Vielzahl fragmentierter Szenarien, Extremsituationen und unvorhersehbares menschliches Verhalten. Der „Long Tail“ von Randszenarien beim autonomen Fahren bezieht sich auf Randfälle in autonomen Fahrzeugen (AVs). Randfälle sind mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. diese seltenen Ereignisse
 Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
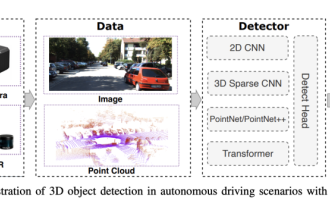
Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
0. Vorab geschrieben&& Persönliches Verständnis, dass autonome Fahrsysteme auf fortschrittlichen Wahrnehmungs-, Entscheidungs- und Steuerungstechnologien beruhen, indem sie verschiedene Sensoren (wie Kameras, Lidar, Radar usw.) verwenden, um die Umgebung wahrzunehmen, und Algorithmen und Modelle verwenden für Echtzeitanalysen und Entscheidungsfindung. Dies ermöglicht es Fahrzeugen, Verkehrszeichen zu erkennen, andere Fahrzeuge zu erkennen und zu verfolgen, das Verhalten von Fußgängern vorherzusagen usw. und sich so sicher an komplexe Verkehrsumgebungen anzupassen. Diese Technologie erregt derzeit große Aufmerksamkeit und gilt als wichtiger Entwicklungsbereich für die Zukunft des Transportwesens . eins. Aber was autonomes Fahren schwierig macht, ist herauszufinden, wie man dem Auto klarmachen kann, was um es herum passiert. Dies erfordert, dass der dreidimensionale Objekterkennungsalgorithmus im autonomen Fahrsystem Objekte in der Umgebung, einschließlich ihrer Standorte, genau wahrnehmen und beschreiben kann.
 Beherrschen Sie die Koordinatensystemkonvertierung wirklich? Multisensorik-Themen, die für das autonome Fahren unverzichtbar sind
Oct 12, 2023 am 11:21 AM
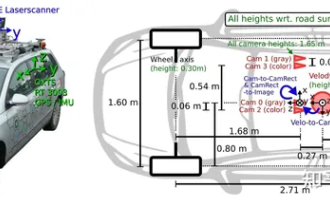
Beherrschen Sie die Koordinatensystemkonvertierung wirklich? Multisensorik-Themen, die für das autonome Fahren unverzichtbar sind
Oct 12, 2023 am 11:21 AM
Der erste Pilot- und Schlüsselartikel stellt hauptsächlich mehrere häufig verwendete Koordinatensysteme in der autonomen Fahrtechnologie vor und erläutert, wie die Korrelation und Konvertierung zwischen ihnen abgeschlossen und schließlich ein einheitliches Umgebungsmodell erstellt werden kann. Der Schwerpunkt liegt hier auf dem Verständnis der Umrechnung vom Fahrzeug in den starren Kamerakörper (externe Parameter), der Kamera-in-Bild-Konvertierung (interne Parameter) und der Bild-in-Pixel-Einheitenkonvertierung. Die Konvertierung von 3D in 2D führt zu entsprechenden Verzerrungen, Verschiebungen usw. Wichtige Punkte: Das Fahrzeugkoordinatensystem und das Kamerakörperkoordinatensystem müssen neu geschrieben werden: Das Ebenenkoordinatensystem und das Pixelkoordinatensystem. Schwierigkeit: Sowohl die Entzerrung als auch die Verzerrungsaddition müssen auf der Bildebene kompensiert werden. 2. Einführung Insgesamt gibt es vier visuelle Systeme Koordinatensystem: Pixelebenenkoordinatensystem (u, v), Bildkoordinatensystem (x, y), Kamerakoordinatensystem () und Weltkoordinatensystem (). Es gibt eine Beziehung zwischen jedem Koordinatensystem,
 Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
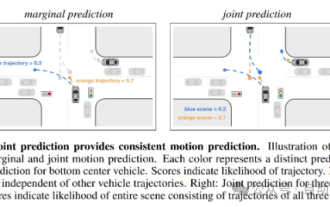
Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Die Trajektorienvorhersage spielt eine wichtige Rolle beim autonomen Fahren. Unter autonomer Fahrtrajektorienvorhersage versteht man die Vorhersage der zukünftigen Fahrtrajektorie des Fahrzeugs durch die Analyse verschiedener Daten während des Fahrvorgangs. Als Kernmodul des autonomen Fahrens ist die Qualität der Trajektorienvorhersage von entscheidender Bedeutung für die nachgelagerte Planungssteuerung. Die Trajektorienvorhersageaufgabe verfügt über einen umfangreichen Technologie-Stack und erfordert Vertrautheit mit der dynamischen/statischen Wahrnehmung des autonomen Fahrens, hochpräzisen Karten, Fahrspurlinien, Fähigkeiten in der neuronalen Netzwerkarchitektur (CNN&GNN&Transformer) usw. Der Einstieg ist sehr schwierig! Viele Fans hoffen, so schnell wie möglich mit der Flugbahnvorhersage beginnen zu können und Fallstricke zu vermeiden. Heute werde ich eine Bestandsaufnahme einiger häufiger Probleme und einführender Lernmethoden für die Flugbahnvorhersage machen! Einführungsbezogenes Wissen 1. Sind die Vorschaupapiere in Ordnung? A: Schauen Sie sich zuerst die Umfrage an, S
 SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
Originaltitel: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper-Link: https://arxiv.org/pdf/2402.02519.pdf Code-Link: https://github.com/HKUST-Aerial-Robotics/SIMPL Autor: Hong Kong University of Science und Technologie DJI-Papieridee: Dieses Papier schlägt eine einfache und effiziente Bewegungsvorhersagebasislinie (SIMPL) für autonome Fahrzeuge vor. Im Vergleich zum herkömmlichen Agent-Cent
 nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
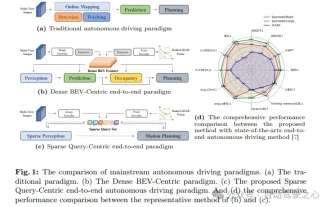
nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
Vorab geschrieben und Ausgangspunkt Das End-to-End-Paradigma verwendet ein einheitliches Framework, um Multitasking in autonomen Fahrsystemen zu erreichen. Trotz der Einfachheit und Klarheit dieses Paradigmas bleibt die Leistung von End-to-End-Methoden für das autonome Fahren bei Teilaufgaben immer noch weit hinter Methoden für einzelne Aufgaben zurück. Gleichzeitig erschweren die in früheren End-to-End-Methoden weit verbreiteten Funktionen der dichten Vogelperspektive (BEV) die Skalierung auf mehr Modalitäten oder Aufgaben. Hier wird ein Sparse-Search-zentriertes End-to-End-Paradigma für autonomes Fahren (SparseAD) vorgeschlagen, bei dem die Sparse-Suche das gesamte Fahrszenario, einschließlich Raum, Zeit und Aufgaben, ohne dichte BEV-Darstellung vollständig abbildet. Insbesondere ist eine einheitliche, spärliche Architektur für die Aufgabenerkennung einschließlich Erkennung, Verfolgung und Online-Zuordnung konzipiert. Zudem schwer
 Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Im vergangenen Monat hatte ich aus bekannten Gründen einen sehr intensiven Austausch mit verschiedenen Lehrern und Mitschülern der Branche. Ein unvermeidliches Thema im Austausch ist natürlich End-to-End und der beliebte Tesla FSDV12. Ich möchte diese Gelegenheit nutzen, einige meiner aktuellen Gedanken und Meinungen als Referenz und Diskussion darzulegen. Wie definiert man ein durchgängiges autonomes Fahrsystem und welche Probleme sollten voraussichtlich durchgängig gelöst werden? Gemäß der traditionellsten Definition bezieht sich ein End-to-End-System auf ein System, das Rohinformationen von Sensoren eingibt und für die Aufgabe relevante Variablen direkt ausgibt. Bei der Bilderkennung kann CNN beispielsweise als End-to-End bezeichnet werden, verglichen mit der herkömmlichen Methode zum Extrahieren von Merkmalen + Klassifizieren. Bei autonomen Fahraufgaben werden Eingabedaten verschiedener Sensoren (Kamera/LiDAR) benötigt



