
Lassen Sie den übergeordneten Knoten den Knoten markieren, der angepasst werden muss, und das untergeordnete Element das linke untergeordnete Element des übergeordneten Knotens markieren (Hinweis: Wenn der übergeordnete Knoten einen Knoten hat).
Wenn das linke Kind des Elternteils vorhanden ist, d , finden Sie das kleinste Kind unter den linken und rechten Kindern und lassen Sie es das Kind markieren
Vergleichen Sie das Elternteil mit dem kleineren Kind, wenn:
Elternteil kleiner als das kleinere Kind ist, endet die Anpassung. Tauschen Sie das übergeordnete Element mit dem kleineren untergeordneten Element aus. Nach Abschluss des Austauschs befindet sich das größere Element im übergeordneten Element. Wenn Sie sich nach unten bewegen, erfüllt der Teilbaum möglicherweise nicht die Eigenschaften des Heaps. Daher muss er weiterhin nach unten angepasst werden, d. h. parent = child; child = parent*2+1 und dann weiter mit Schritt 2.
public void shiftDown(int[] elem,int parent,int len){
int cur=parent*2+1;
while(cur<len){
if(cur+1<len){
if(elem[cur+1]<elem[cur]){
cur++;
}
}
if(this.elem[cur]<this.elem[parent]) {
swap(cur, parent);
}
parent=cur;
cur=parent*2+1;
}
}Für eine normale Sequenz müssen wir mit der Anpassung vom ersten übergeordneten Knoten mit einem linken Knoten beginnen, bis der gesamte Baum die Eigenschaften eines Heaps erfüllt.
3. Zeitaufwand für die Erstellung eines Heaps Der Heap muss ein vollständiger Binärbaum sein, und ein vollständiger Binärbaum ist auch ein vollständiger Binärbaum. Aus der folgenden Berechnung ergibt sich, dass die Zeitkomplexität für die Erstellung eines Heaps O(n) ist Heap, wenn es nicht freigegeben werden kann, erweitern Sie die Kapazität.
Der Heap muss ein vollständiger Binärbaum sein, und ein vollständiger Binärbaum ist auch ein vollständiger Binärbaum. Aus der folgenden Berechnung ergibt sich, dass die Zeitkomplexität für die Erstellung eines Heaps O(n) ist Heap, wenn es nicht freigegeben werden kann, erweitern Sie die Kapazität.
Passen Sie den neu eingefügten Knoten nach oben an, bis er den Eigenschaften des Heaps entspricht
Entsprechend den Eigenschaften des Heaps muss das oberste Element des Heaps gelöscht werden. Die Schritte sind wie folgt:
 3. Heap-Anwendung
3. Heap-Anwendung
1. Heap-Sortierung
Absteigende Reihenfolge: Erstellen Sie einen kleinen Root-Heap , und nach unten anpassen, bis der Haufen in Ordnung ist.
public void shiftUp(int elem[],int child){
int parent=(child-1)/2;
while(parent>=0){
if(elem[child]>elem[parent]){
swap(child,parent);
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}IV. Einführung in gängige Schnittstellen
Das Java-Collection-Framework bietet zwei Arten von Prioritätswarteschlangen: PriorityQueue und PriorityBlockingQueue. PriorityQueue ist Thread-unsicher und PriorityBlockingQueue ist Thread-sicher. In diesem Artikel wird hauptsächlich PriorityQueue vorgestellt. 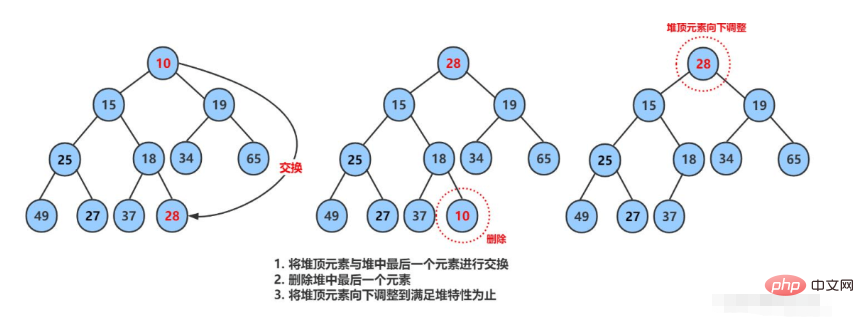
 kann keine Nullelemente platzieren , NullPointerException wird ausgelöst;
kann keine Nullelemente platzieren , NullPointerException wird ausgelöst;
Sie können so viele Elemente einfügen, wie Sie möchten, und die interne Kapazität wird automatisch erweitert

Wenn die Kapazität MAX_ARRAY_SIZE überschreitet, erweitern Sie die Kapazität entsprechend MAX_ARRAY_SIZE
(oldCapacity + 2) :
// 用户自己定义的比较器:直接实现Comparator接口,然后重写该接口中的compare方法即可
class IntCmp implements Comparator<Integer>{
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
}
PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());| 构造器 | 功能介绍 |
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) |
创建一个初始容量为initialCapacity的优先级队列,注意: initialCapacity不能小于1,否则会抛IllegalArgumentException异 常 |
| PriorityQueue(Collection extends E> c) |
用一个集合来创建优先级队列 |
Das obige ist der detaillierte Inhalt vonEinführung in Anwendungsszenarien und Implementierungsmethoden von Java Heap. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




