Nach vier Monaten wurde eine weitere Gemeinschaftsarbeit zwischen ByteDance Research und Chen Jis Forschungsgruppe an der School of Physics der Peking-Universität in internationalen Top-Publikationen Nature Communications veröffentlicht: Der Artikel „Towards the Ground State of Molecules via Diffusion Monte Carlo über neuronale Netze 》Die Kombination des neuronalen Netzes mit der Diffusions-Monte-Carlo-Methode verbessert die Rechengenauigkeit, Effizienz und Systemskala der neuronalen Netzmethode bei quantenchemischen Aufgaben erheblich und wird zum neuesten SOTA.
- Link zum Papier:
https://www.nature.com/articles/s41467-023-37609-3 - Code-Adresse:
https://github.com/bytedance/jaqmc
Einführung
Der Autor wendet die auf einem neuronalen Netzwerk basierende Testwellenfunktion auf die Diffusions-Monte-Carlo-Methode der festen Knotenoberfläche an ( Diffusion Monte Carlo oder DMC), wird zur genauen Berechnung atomarer und molekularer Systeme mit unterschiedlichen elektronischen Eigenschaften verwendet.
Die Diffusions-Monte-Carlo-Methode ist eine der am häufigsten verwendeten Methoden auf dem Gebiet der Quantenchemie, um die Grundzustandsenergie von Molekülen und Materialien genau zu berechnen. Durch die Kombination mit der Diffusions-Monte-Carlo-Methode verbesserten die Autoren die Rechengenauigkeit und Effizienz der SOTA-Methode des neuronalen Netzwerks in der Quantenchemie erheblich. Darüber hinaus schlug der Autor auch eine Extrapolationsmethode vor, die auf empirischen linearen Beziehungen basiert und die Berechnung der molekularen Bindungsenergie erheblich verbessert. Insgesamt dient dieser Rechenrahmen als hochpräzise Methode zur Lösung von Quanten-Vielteilchenproblemen und stellt ein leistungsfähigeres Werkzeug für ein tieferes Verständnis der Eigenschaften chemischer Moleküle dar.
Quanten-Monte-Carlo-Methode basierend auf neuronalen Netzwerken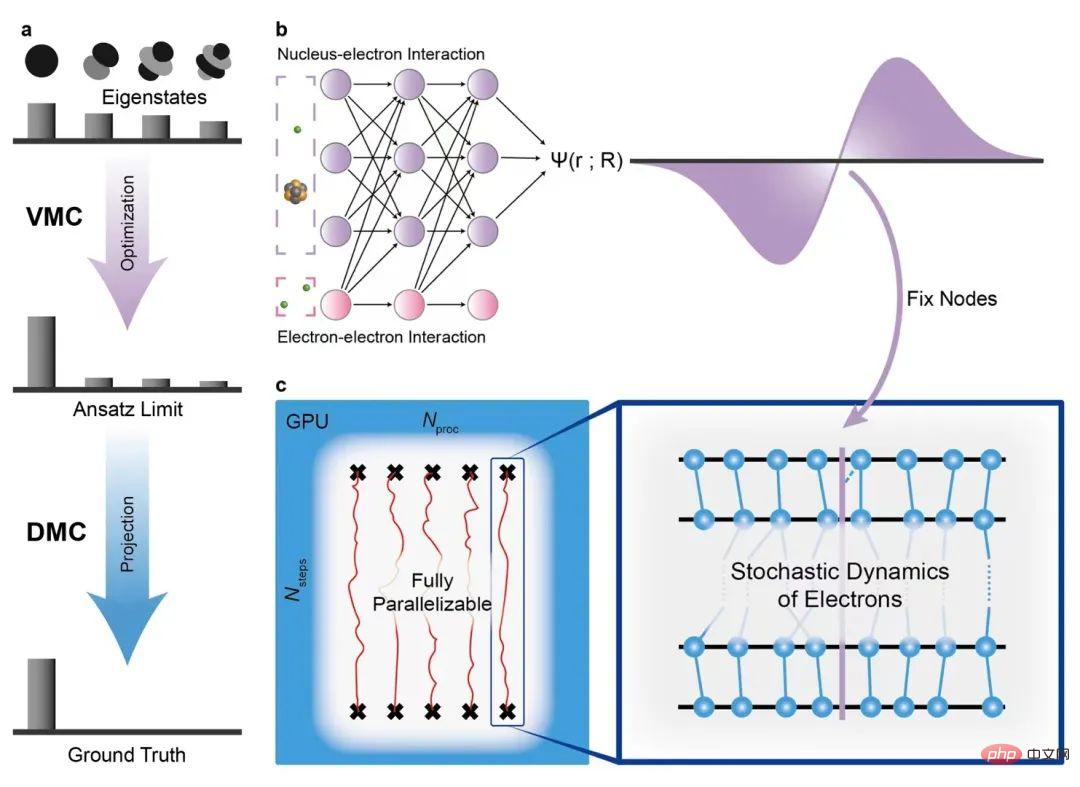
Seit 2018 haben mehrere Forschungsgruppen neuronale Netzwerke auf die Variations-Monte-Carlo-Methode (Variational Monte Carlo oder VMC) [1,2,3] angewendet Mit Hilfe der leistungsstarken Expressionsfähigkeit neuronaler Netze wird eine genauere molekulare Grundzustandsenergie erhalten. Als diese Arbeit im Jahr 2022 veröffentlicht wurde, war die SOTA-Arbeit in der auf neuronalen Netzwerken basierenden Variations-Monte-Carlo-Methode FermiNet [2], die 2019 von DeepMind vorgeschlagen wurde und sehr genaue Ergebnisse auf einem kleineren System erzielen konnte. Die Genauigkeit der Variations-Monte-Carlo-Methode ist jedoch durch die Ausdrucksfähigkeit des neuronalen Netzwerks begrenzt, und beim Umgang mit größeren Systemen treten immer offensichtlichere Genauigkeitsprobleme auf. Darüber hinaus konvergiert diese Art von Methode bei größeren Systemen sehr langsam, was eine große Herausforderung für die Rechenressourcen darstellt.
Als einer der klassischen hochpräzisen Algorithmen auf dem Gebiet der Quantenchemie weist die Diffusions-Monte-Carlo-Methode gute Eigenschaften wie hohe Genauigkeit, gute Parallelisierbarkeit und Eignung für groß angelegte Berechnungen auf. Darüber hinaus kann Diffusions-Monte-Carlo die Einschränkungen der Ausdrucksfähigkeit neuronaler Netze durchbrechen und mithilfe von Projektionsalgorithmen die Genauigkeit der Variations-Monte-Carlo-Methode übertreffen.
In dieser Arbeit kombiniert der Autor das neuronale Netzwerk von SOTA (FermiNet) als Testwellenfunktion mit der Diffusions-Monte-Carlo-Methode. Die neue Berechnungsmethode verbessert die Genauigkeit deutlich und reduziert die Anzahl der erforderlichen Berechnungsschritte im Vergleich zu FermiNet. Die in dieser Arbeit entworfene und implementierte Diffusions-Monte-Carlo-Software ist für neuronale Netzwerke, GPUs und Parallelen geeignet. Sie kann mit einer Vielzahl neuronaler Netzwerkwellenfunktionen kombiniert werden, um ihre Genauigkeit und Effizienz automatisch zu verbessern. 1. Atome Die Verwendung unterliegt ebenfalls bestimmten Einschränkungen. Um dieses Szenario zu simulieren, verwendeten die Autoren nur zwei Schichten neuronaler Netze, um die zweite und dritte Atomreihe zu untersuchen. Die Berechnungsergebnisse zeigen, dass mit zunehmender Systemgröße die Genauigkeit der Variations-Monte-Carlo-Methode immer schlechter wird, während die Genauigkeitsverbesserung durch die Diffusions-Monte-Carlo-Methode immer offensichtlicher wird.
2
Der Autor verifizierte auch die Wirksamkeit der auf einem neuronalen Netzwerk basierenden Diffusions-Monte-Carlo-Methode an einer Reihe molekularer Systeme, darunter Stickstoffmoleküle, Cyclobutadien und Doppelwassermoleküle. Auf allen getesteten Systemen wurden deutliche Verbesserungen der Rechengenauigkeit beobachtet. 3. Benzol-Ring und Diphenyl-Ring Elektronen oder weniger Kleine Moleküle. Diese Arbeit wendet die Wellenfunktionsmethode des neuronalen Netzwerks erstmals auf Systeme mit 42 bis 84 Elektronen an, nämlich Benzolringe und Biphenylringe. Die Berechnungsergebnisse zeigen, dass die Diffusions-Monte-Carlo-Methode hinsichtlich der Genauigkeit deutlich besser ist als die Variations-Monte-Carlo-Methode und mit einer Größenordnung weniger Berechnungsschritten die gleiche oder eine bessere Genauigkeit erreichen kann.
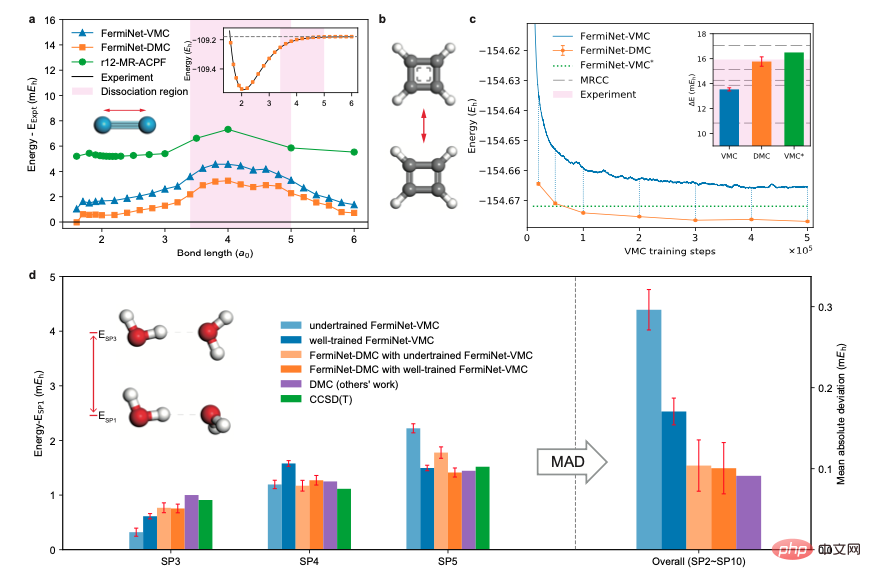
4. Lineare Beziehung und Extrapolationsmethode
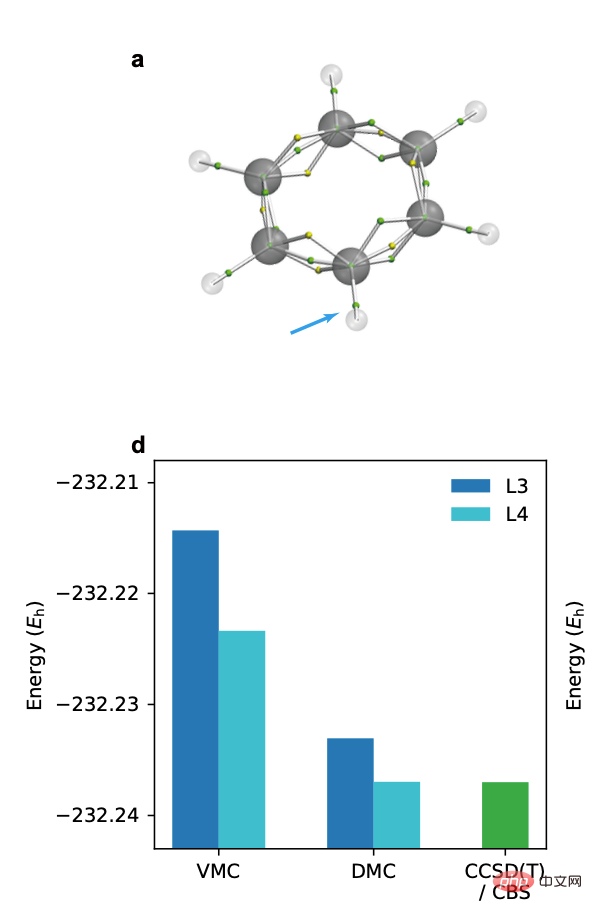
Als der Autor die Energie untersuchte, die verschiedenen Trainingsstadien des neuronalen Netzwerks entspricht, wurden in vielen Systemen Variationen festgestellt Die Berechnung Die Ergebnisse von Monte Carlo und Diffusion Monte Carlo stehen in einem empirischen linearen Zusammenhang (linke Abbildung unten). Die Verwendung dieser linearen Beziehung zur Extrapolation der Dissoziationsenergieberechnung des Biphenylrings verbesserte die Berechnungsgenauigkeit erheblich und lieferte Ergebnisse, die mit chemischen Experimenten übereinstimmten (rechtes Bild unten).
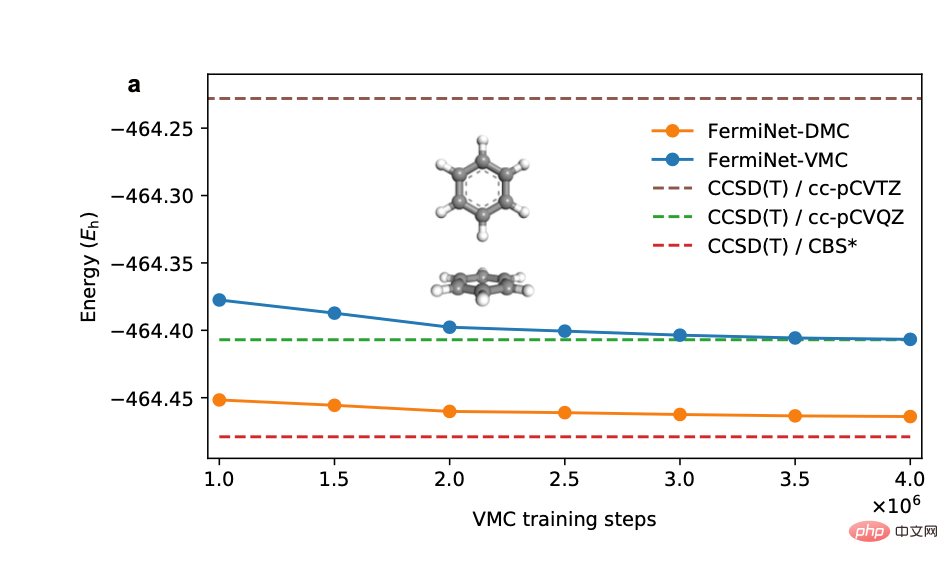
Fazit und AusblickDiese Arbeit zeigt, dass die auf neuronalen Netzen basierende Diffusions-Monte-Carlo-Methode der Variations-Monte-Carlo-Methode sowohl hinsichtlich Genauigkeit als auch Effizienz überlegen ist. Der Open-Source-Monte-Carlo-Code des Autors kann schnell mit den ständig innovativen neuronalen Netzen [4,5] im Bereich der Quantenchemie kombiniert werden, um die Forschungsgemeinschaft zu stärken. Darüber hinaus kann die Diffusions-Monte-Carlo-Methode auch mit einer Reihe von Methoden wie periodischen neuronalen Netzen [6] und neuronalen Netzen mit Pseudopotentialen [7] kombiniert werden, die sich mit realen Festkörpern befassen, um die Recheneffekte bei entsprechenden Aufgaben zu verbessern.
Das obige ist der detaillierte Inhalt vonNeue Forschungsergebnisse zeigen das Potenzial von Quanten-Monte-Carlo, neuronale Netze bei der Überwindung von Beschränkungen zu übertreffen, und eine Unterausgabe von Nature beschreibt die neuesten Fortschritte. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
