Was ist die Implementierungsmethode des KMP-Algorithmus in Java?

Abbildung

Der kmp-Algorithmus weist eine gewisse Ähnlichkeit mit der zuvor erwähnten Idee des bm-Algorithmus auf. Wie bereits erwähnt, gibt es das Konzept eines guten Suffixes im bm-Algorithmus und es gibt ein Konzept eines guten Präfixes in kmp. Schauen wir uns zunächst das folgende Beispiel an.

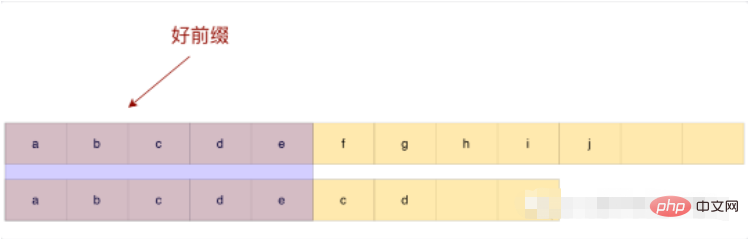
Beobachten Sie das obige Beispiel: Das bereits übereinstimmende abcde wird als gutes Präfix bezeichnet, a stimmt nicht mit dem folgenden bcde überein, sodass kein erneuter Vergleich erforderlich ist. Schieben Sie es einfach direkt nach e.

Was ist, wenn das gute Präfix übereinstimmende Zeichen enthält?

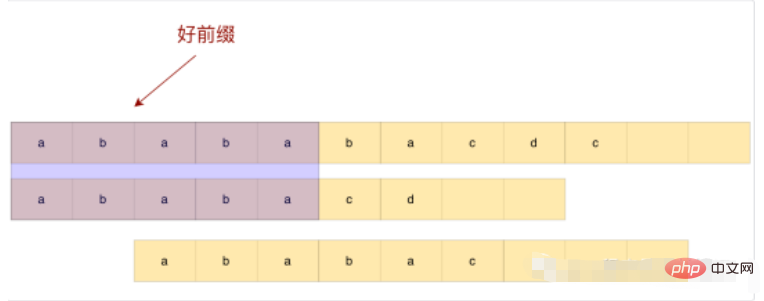
Beobachten Sie das obige Beispiel. Wenn wir zu diesem Zeitpunkt direkt nach dem guten Präfix schieben, schieben wir zu viel und verpassen den passenden Teilstring. Wie führen wir also ein vernünftiges Gleiten basierend auf guten Präfixen durch?

Tatsächlich wird überprüft, ob das Präfix und das Suffix des aktuellen guten Präfixes übereinstimmen, die längste passende Länge gefunden und direkt verschoben. Um die längste passende Länge mehr als einmal zu finden, können wir zuerst ein Array initialisieren und die längste passende Länge unter dem aktuellen guten Präfix speichern. Zu diesem Zeitpunkt wird unser nächstes Array ausgegeben.

Wir definieren ein nächstes Array, das die längste übereinstimmende Teilzeichenfolgenlänge des Präfixes und Suffixes des guten Präfixes unter dem aktuellen guten Präfix darstellt. Diese längste übereinstimmende Länge bedeutet, dass diese Teilzeichenfolge bereits zuvor abgeglichen wurde und nicht erneut abgeglichen werden muss . Der Abgleich beginnt direkt mit dem nächsten Zeichen der Teilzeichenfolge.

Müssen wir bei jeder Berechnung von next[i] jedes Zeichen abgleichen? Können wir aus next[i - 1] schließen, um unnötige Vergleiche zu vermeiden?

Mit dieser Idee werfen wir einen Blick auf die folgenden Schritte:

Angenommen, next[i - 1] = k - 1;

Wenn modelStr[k] = modelStr[i], dann next[i]=k

Wenn modelStr[k] != modelStr[i], können wir dann direkt next[i] = next[i - 1] bestimmen?

Anhand des obigen Beispiels können wir deutlich erkennen, dass next[i]!=next[i-1] dann, wenn modelStr[k]!=modelStr[i], bereits next[ 0],next kennt [1]…next[i-1], wie kann man next[i] herausschieben?

Angenommen, modelStr[x…i] ist die längste Suffix-Teilzeichenfolge, mit der das Präfix und das Suffix übereinstimmen können, dann ist die längste passende Präfix-Teilzeichenfolge modelStr[0…i-x]

Wenn wir die längste passende Zeichenfolge finden, ist sie die vorherige Die zweitlängste übereinstimmende Zeichenfolge (mit Ausnahme des aktuellen i), d ist modelStr[0…i-x-1], die Suffix-Teilzeichenfolge ist modelStr[x…i-1] und modelStr[i-x] == modelStr[i], diese Präfix-Suffix-Teilzeichenfolge ist die sekundäre Präfix-Teilzeichenfolge plus das aktuelle Zeichen ist die längste passende Präfix- und Suffix-Teilzeichenfolge.

Code-Implementierung

Zunächst das wichtigste nächste Array im kmp-Algorithmus. Dieses Array markiert die Anzahl der längsten Präfix- und Suffixzeichen, die im kmp-Algorithmus übereinstimmen ​ein gutes Präfix, das heißt: Durch Anpassen des Musterzeichenfolgenpräfixes können wir bestimmte Techniken verwenden, um mehr als ein Zeichen nach vorne zu schieben. Weitere Informationen finden Sie in der vorherigen Erklärung. Wir wissen nicht im Voraus, welche Präfixe gut sind, und der Abgleichvorgang erfolgt mehr als einmal. Daher rufen wir zu Beginn eine Initialisierungsmethode auf, um das nächste Array zu initialisieren.

1. Wenn das nächste Zeichen der längsten Präfix-Teilzeichenfolge des vorherigen Zeichens == das aktuelle Zeichen ist, kann die längste Präfix-Teilzeichenfolge des vorherigen Zeichens direkt zum aktuellen Zeichen hinzugefügt werden

2 Wenn es nicht gleich ist Sie müssen das vorherige Zeichen finden. Das nächste Zeichen der längsten vorhandenen Präfix-Teilzeichenfolge ist gleich der aktuellen Teilzeichenfolge und legt dann die längste Präfix-Suffix-Teilzeichenfolge der aktuellen Zeichen-Teilzeichenfolge fest

int[] next ;
    /**
     * 初始化next数组
     * @param modelStr
     */
    public void init(char[] modelStr) {
        //首先计算next数组
        //遍历modelStr，遍历到的字符与之前字符组成一个串
        next = new int[modelStr.length];
        int start = 0;
        while (start < modelStr.length) {
            next[start] = this.recursion(start, modelStr);
            ++ start;
        }
    }

    /**
     *
     * @param i 当前遍历到的字符
     * @return
     */
    private int recursion(int i, char[] modelStr) {
        //next记录的是个数，不是下标
        if (0 == i) {
            return 0;
        }
        int last = next[i -1];
        //没有匹配的,直接判断第一个是否匹配
        if (0 == last) {
            if (modelStr[last] == modelStr[i]) {
                return 1;
            }
            return 0;
        }
        //如果last不为0，有值，可以作为最长匹配的前缀
        if (modelStr[last] == modelStr[i]) {
            return next[i - 1] + 1;
        }
        //当next[i-1]对应的子串的下一个值与modelStr不匹配时，需要找到当前要找的最长匹配子串的次长子串
        //依据就是次长子串对应的子串的下一个字符==modelStr[i];
        int tempIndex = i;
        while (tempIndex > 0) {
            last = next[tempIndex - 1];
            //找到第一个下一个字符是当前字符的匹配子串
            if (modelStr[last] == modelStr[i]) {
                return last + 1;
            }
            -- tempIndex;
        }
        return 0;
    }

Beginnen Sie dann mit der Verwendung des nächsten übereinstimmenden Arrays, beginnend mit Finden Sie das erste nicht übereinstimmende Zeichen. Beurteilen Sie zunächst, ob es sich um eine vollständige Übereinstimmung handelt, und geben Sie es direkt zurück. und dann passt es direkt zur Rückseite. Wenn ein gutes Präfix vorhanden ist, wird zu diesem Zeitpunkt das nächste Array verwendet. Durch das nächste Array wissen wir, wo der aktuelle Abgleich beginnen kann, und es besteht keine Notwendigkeit, die vorherigen abzugleichen.

public int kmp(char[] mainStr, char[] modelStr) {
        //开始进行匹配
        int i = 0, j = 0;
        while (i + modelStr.length <= mainStr.length) {
            while (j < modelStr.length) {
                //找到第一个不匹配的位置
                if (modelStr[j] != mainStr[i]) {
                    break;
                }
                ++ i;
                ++ j;
            }
            if (j == modelStr.length) {
                //证明完全匹配
                return i - j;
            }
            //走到这里找到的是第一个不匹配的位置
            if (j == 0) {
                ++ i;
                continue;
            }
            //从好前缀后一个匹配
            j = next[j - 1];
        }
        return -1;
    }

Das obige ist der detaillierte Inhalt vonWas ist die Implementierungsmethode des KMP-Algorithmus in Java?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!