
Ein Baum ist ein ungerichteter Graph, in dem zwei beliebige Eckpunkte nur durch einen Pfad verbunden sind. Mit anderen Worten: Jeder zusammenhängende Graph ohne einfache Zyklen ist ein Baum.
Sie erhalten einen Baum mit n Knoten mit der Bezeichnung 0 bis n - 1. Gegeben sei eine Zahl n und eine Kantenliste mit n - 1 ungerichteten Kanten (jede Kante ist ein Beschriftungspaar), wobei Kanten[i] = [ai, bi] bedeutet, dass es eine Kante zwischen den Knoten ai und bi im Baum gibt Ungerichtet Rand.
Sie können jeden Knoten im Baum als Wurzel auswählen. Wenn Knoten x als Wurzelknoten ausgewählt wird, sei die Höhe des Ergebnisbaums h. Unter allen möglichen Bäumen wird der Baum mit der minimalen Höhe (d. h. min(h)) als Baum mit minimaler Höhe bezeichnet.
Bitte suchen Sie alle Bäume mit Mindesthöhe und geben Sie deren Wurzelknotenbeschriftungsliste in beliebiger Reihenfolge zurück.
Die Höhe eines Baumes bezieht sich auf die Anzahl der Kanten auf dem längsten Abwärtspfad zwischen dem Wurzelknoten und den Blattknoten.
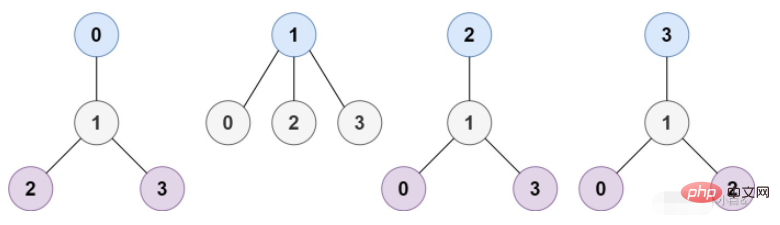
Eingabe: n = 4, Kanten = [[1,0],[1,2],[1,3]]
Ausgabe: [1]
Erklärung: Wie in der gezeigt Abbildung: Wenn die Wurzel der Knoten mit der Bezeichnung 1 ist, beträgt die Höhe des Baums 1, was die einzige Mindesthöhe des Baums darstellt.
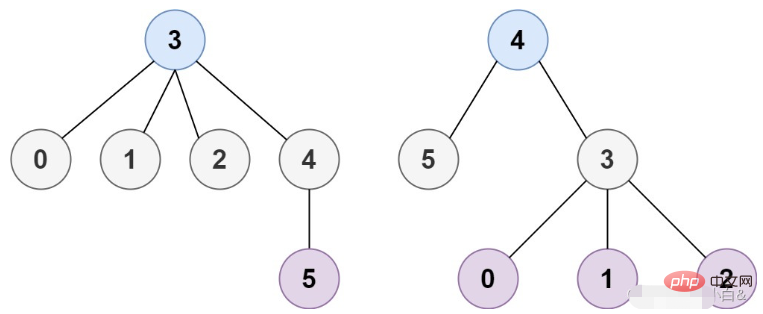
Eingabe: n = 6, Kanten = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Ausgabe: [3,4]
Eingabeaufforderung:
1 edges.length == n - 1
0 ai != bi
Alle (ai, bi) unterscheiden sich voneinander
Die gegebene Eingabe ist garantiert ein Baum und es gibt keine doppelten Kanten
Aus den beiden obigen Abbildungen: Wir können eine Schlussfolgerung ziehen: Was in der Frage gelöst werden muss, ist der zentrale Knoten im Baum, und jeder Baum wird nicht mehr als zwei zentrale Knoten haben.
Und wenn wir den zentralen Knoten im Baum erhalten möchten, können wir Schicht für Schicht FBS durchführen (d. h. die Blattknoten mit einem Out-Grad von eins Schicht für Schicht abschneiden), bis die letzte Schicht erreicht ist schneiden, dann können wir das Ergebnis ausgeben!
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
List<Integer> res = new ArrayList<Integer>();
//如果只有一个节点,则它就是最小高度树
if(n == 1){
res.add(0);
return res;
}
//每个节点的邻居数量
int [] degree = new int[n];
//每个节点的邻居
HashMap<Integer,List<Integer>> map = new HashMap<>();
for(int [] edge : edges){
int a = edge[0];
int b = edge[1];
degree[a]++;
degree[b]++;
if(map.get(a) == null){
map.put(a,new ArrayList<Integer>());//key:节点 value:邻居
}
if(map.get(b) == null){
map.put(b,new ArrayList<Integer>());//key:节点 value:邻居
}
map.get(a).add(b);
map.get(b).add(a);
}
//建立队列
LinkedList<Integer> leafNodes = new LinkedList<Integer>();//表示叶子节点
//将所有度为1的节点入队
for(int i = 0;i < degree.length;i++){
if(degree[i] == 1){
leafNodes.add(i);
}
}
while(leafNodes.size() > 0){
res.clear();
//每一层节点的数量
int size = leafNodes.size();
for(int i = 0;i < size;i++){
int leaf = leafNodes.poll();
//将当前节点加入到结果集
res.add(leaf);
List<Integer> neighbors = map.get(leaf);
//将出度减一,也就是将最外层的叶子节点剪掉
for(int neighbor : neighbors){
degree[neighbor]--;
if(degree[neighbor] == 1){
//叶子节点入队
leafNodes.add(neighbor);
}
}
}
}
return res;
}
}Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen Baum mit minimaler Höhe in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




