So implementieren Sie gängige Sortieralgorithmen in Java

Zusammenfassung:

1. Blasensortierung

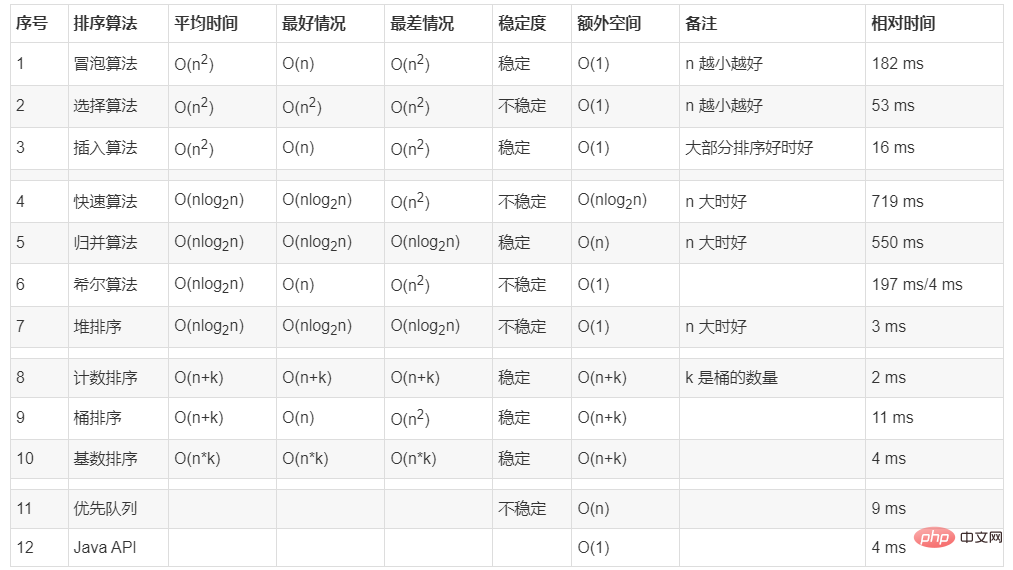
#🎜🎜 # Bestimmen Sie den besten Wert in jeder Runde der Schleife die Kante;

public void bubbleSort(int[] nums){
    int temp;
    boolean isSort = false; //优化，发现排序好就退出
    for (int i = 0; i < nums.length-1; i++) {
        for (int j = 0; j < nums.length-1-i; j++) {  //每次排序后能确定较大值
            if(nums[j] > nums[j+1]){
                isSort = true;
                temp = nums[j];
                nums[j] = nums[j+1];
                nums[j+1] = temp;
            }
        }
        if(!isSort){
            return;
        } else {
            isSort = false;
        }
    }
}

3. Einfügungssortierung

Finden Sie eine eigene Position für jede einzufügende Zahl; 🎜🎜#

public void selectSort(int[] nums){
    for (int i = 0; i < nums.length-1; i++) {
        int index = i;
        int minNum = nums[i];
        for (int j = i+1; j < nums.length; j++) {
            if(nums[j] < minNum){
                minNum = nums[j];
                index = j;
            }
        }
        if(index != i){
            nums[index] = nums[i];
            nums[i] = minNum;
        }
    }
}

4. Schnelle Sortierung

Wählen Sie einen Grundwert, geben Sie den kleineren Wert auf die eine Seite und den größeren Wert auf die andere Seite. 🎜🎜#

public void insertionSort(int[] nums){
    for (int i = 1; i < nums.length; i++) {
        int j = i;
        int insertNum = nums[i];
        while(j-1 >= 0 && nums[j-1] > insertNum){
            nums[j] = nums[j-1];
            j--;
        }
        nums[j] = insertNum;
    }
}

#🎜 5. Merge-Sortierung

Einführung der Schrittgröße, um die Anzahl der digitalen Austausche zu reduzieren und die Effizienz zu verbessern; 🎜🎜#

6.1 Hill-Bubble-Sortierung (langsam)

public void quickSortDfs(int[] nums, int left, int right){
    if(left > right){
        return;
    }
    int l = left;
    int r = right;
    int baseNum = nums[left];
    while(l < r){
        //必须右边先走
        while(nums[r] >= baseNum && l < r){
            r--;
        }
        while(nums[l] <= baseNum && l < r){
            l++;
        }
        int temp = nums[l];
        nums[l] = nums[r];
        nums[r] = temp;
    }
    nums[left] = nums[l];
    nums[l] = baseNum;
    quickSortDfs(nums, left, r-1);
    quickSortDfs(nums, l+1, right);
}

6.2 Hill-insertion-Sortierung (schnell)

//归
public void mergeSortDfs(int[] nums, int l, int r){
    if(l >= r){
        return;
    }
    int m = (l+r)/2;
    mergeSortDfs(nums, l, m);
    mergeSortDfs(nums, m+1, r);
    merge(nums, l, m, r);
}
//并
private void merge(int[] nums, int left, int mid, int right){
    int[] temp = new int[right-left+1];
    int l = left;
    int m = mid+1;
    int i = 0;
    while(l <= mid && m <= right){
        if(nums[l] < nums[m]){
            temp[i++] = nums[l++];
        } else {
            temp[i++] = nums[m++];
        }
    }
    while(l <= mid){
        temp[i++] = nums[l++];
    }
    while(m <= right){
        temp[i++] = nums[m++];
    }
    System.arraycopy(temp, 0, nums, left, temp.length);
}

7. 🎜🎜#

Big Top Heap implementiert eine aufsteigende Reihenfolge, wobei der Maximalwert jedes Mal an die letzte Position des Heaps verschoben wird; #

public void shellBubbleSort(int[] nums){
    for (int step = nums.length/2; step > 0 ; step /= 2) {
        for (int i = step; i < nums.length; i++) {
            for (int j = i-step; j >= 0; j -= step) {
                if(nums[j] > nums[j+step]){
                    int temp = nums[j];
                    nums[j] = nums[j+step];
                    nums[j+step] = temp;
                }
            }
        }
    }
}

8. 🎜🎜#

Zählen Sie die Anzahl der Vorkommen jeder Zahl der Reihe nach; # ähnelt der Zählsortierung, der Unterschied besteht jedoch darin, dass die Zahlen in einem bestimmten Intervall (Bucket) gezählt werden. 🎜🎜# Sortieren nach Einer, Zehner und Hunderter; 🎜#11.1 Prioritätswarteschlange

public void shellInsertSort(int[] nums){
    for (int step = nums.length/2; step > 0; step /= 2) {
        for (int i = step; i < nums.length; i++) {
            int j = i;
            int insertNum = nums[i];
            while(j-step >= 0 && nums[j-step] > insertNum){
                nums[j] = nums[j-step];
                j-=step;
            }
            nums[j] = insertNum;
        }
    }
}

11.2 Java API

public void heapSort2(int[] nums) {
    for(int i = nums.length/2-1; i >= 0; i--){
        sift(nums, i, nums.length);
    }
    for (int i = nums.length-1; i > 0; i--) {
        int temp = nums[0];
        nums[0] = nums[i];
        nums[i] = temp;
        sift(nums, 0, i);
    }
}
private void sift(int[] nums, int parent, int len) {
    int value = nums[parent];
    for (int child = 2*parent +1; child < len; child = child*2 +1) {
        if(child+1 < len && nums[child+1] > nums[child]){
            child++;
        }
        if(nums[child] > value){
            nums[parent] = nums[child];
            parent = child;
        } else {
            break;
        }
    }
    nums[parent] = value;
}

Das obige ist der detaillierte Inhalt vonSo implementieren Sie gängige Sortieralgorithmen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!