Der Heap, auch Prioritätswarteschlange genannt, ist ein vollständiger Binärbaum, und der Wert jedes seiner übergeordneten Knoten ist nur kleiner oder gleich (den Werten von) alle untergeordneten Knoten. Dazu wird ein Array verwendet: Von Null an gezählt, gibt es für alle k heap[k] . Aus Vergleichsgründen werden nicht existierende Elemente als unendlich betrachtet. Das interessanteste Merkmal des Heaps ist, dass sich das kleinste Element immer am Wurzelknoten befindet: Heap[0].
Pythons Heap ist im Allgemeinen ein minimaler Heap, der sich vom Inhalt in vielen Lehrbüchern unterscheidet. Da der Heap von oben nach unten und von links nach rechts ausgedrückt wird, ist er einer Liste sehr ähnlich Um einen Heap zu erstellen, können Sie eine Liste verwenden, um ihn als [] zu initialisieren, oder Sie können eine Funktion heapify() verwenden, um eine Liste in einen Heap umzuwandeln. Das Folgende sind verwandte Vorgänge auf dem Heap in Python. Daraus ist ersichtlich, dass Python den Heap als Liste behandelt.
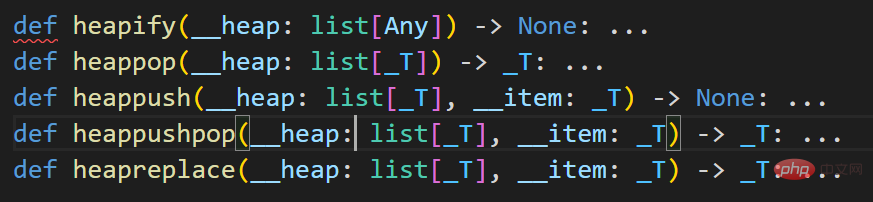
Füge den Wert von item zum Heap hinzu, um die Invarianz des Heaps aufrechtzuerhalten. Es tauscht automatisch verwandte Elemente gemäß der Funktion „Minimum-Heap“ in Python aus, sodass das Stammknotenelement des Heaps niemals größer als die untergeordneten Knotenelemente ist.
Die Originaldaten sind ein Haufen
import heapq h = [1, 2, 3, 5, 7] heapq.heappush(h, 2) print(h) #输出 [1, 2, 2, 5, 7, 3]
Der Vorgang ist wie folgt:
1. Nach dem Hinzufügen von 2 Elementen ist Folgendes zu sehen: Da es die Mindestheap-Eigenschaften nicht erfüllt, wird der Austausch mit 3
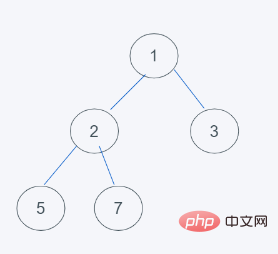
4 durchgeführt. In Übereinstimmung mit den Mindestheap-Eigenschaften endet der Austausch, sodass das Ergebnis [1, 2, 3, 5, 7, 3]
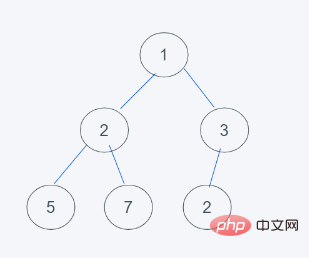Die Originaldaten sind kein Heap
import heapq h = [5, 2, 1, 4, 7] heapq.heappush(h, 2) print(h) #输出 [5, 2, 1, 4, 7, 2]
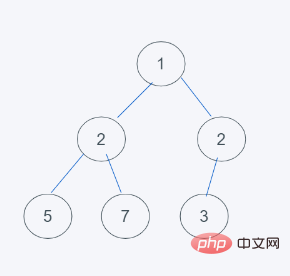heapq.heappop(heap)
poppt und gibt das kleinste Element des Heaps zurück, wobei die Unveränderlichkeit des Heaps erhalten bleibt. Wenn der Heap leer ist, wird IndexError ausgelöst. Mit heap[0] ist es möglich, nur auf das kleinste Element zuzugreifen, ohne es zu löschen.
Die Originaldaten sind ein Heap
import heapq h = [1, 2, 3, 5, 7] heapq.heappop(h) print(h) #输出 [2, 5, 3, 7]
1. Ausgangszustand
2. Das oberste Element des Heaps wird gelöscht an die Spitze des Heaps
3. Tauschen Sie Elemente entsprechend den Merkmalen des Python-Minimums aus. Da 7>2, tauschen Sie 7 und 2 aus Heap. Weil 7>5, tauschen Sie 7 und 5 aus
import heapq h = [5, 2, 1, 4, 7] heapq.heappop(h) print(h) [1, 2, 7, 4]
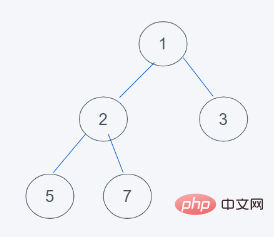Der Vorgang ist wie folgt: 1. Der Ausgangszustand entspricht offensichtlich nicht den Eigenschaften des Heaps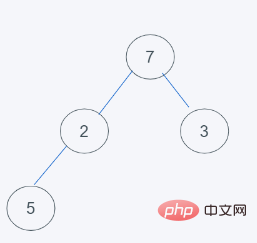 
2. Entfernen Sie das oberste Element (das erste Element) und ordnen Sie die verbleibenden Elemente neu an im Heap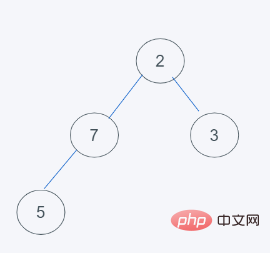
3. Gemäß den Eigenschaften des minimalen Heaps von Python tauscht 2>1 2 und 1 aus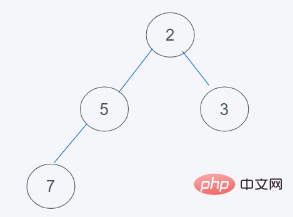
4 Erfüllt die Anforderungen des Heaps, das Ergebnis ist [1, 2, 7, 4]heapq.heappushpop(heap, item)
Legen Sie das Element in den Heap, öffnen Sie es und geben Sie den Mindestwert des Heap-Elements zurück. Diese kombinierte Operation läuft effizienter, als zuerst heappush() und dann heappop() aufzurufen. Es ist zu beachten, dass sich das eingefügte Element am Anfang oder am Ende des Heaps befinden muss. Das heißt, wenn ein Element eingefügt wird und das kleinste Element verglichen wird, wird immer das oberste Element des Heaps verglichen größer oder gleich dem obersten Element des Heaps ist. Der Heap ändert sich nicht. Wenn das eingefügte Element kleiner als das oberste Element des Heaps ist, wird der Heap gemäß den minimalen Heap-Eigenschaften des Python-Heaps verarbeitet. Die Originaldaten sind ein Haufen
import heapq h = [1, 2, 3, 5, 7] min_data = heapq.heappushpop(h, 2) print(min_data) print(h) #输出 1 [2, 2, 3, 5, 7]
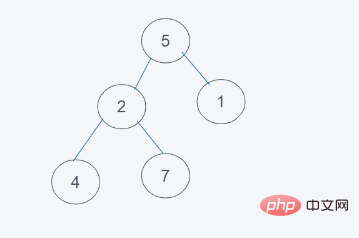
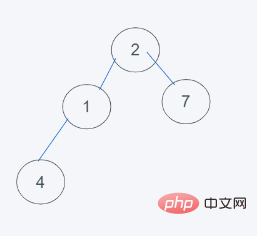
3.删除最小元素，刚好是堆顶元素1，并使用末尾元素2代替
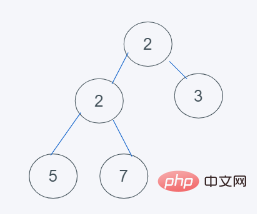
4.符合要求，即结果为[2, 2, 3, 5, 7]
原有数据不是堆
h = [5, 2, 1, 4, 7] min_data = heapq.heappushpop(h, 2) print(min_data) print(h) min_data = heapq.heappushpop(h, 6) print(min_data) print(h) #输出 2 [5, 2, 1, 4, 7] 5 [1, 2, 6, 4, 7]
对于插入元素6的操作过程如下
1.初始状态
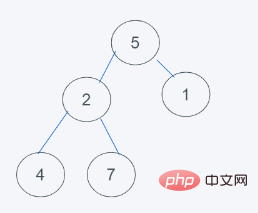
2.插入元素6之后
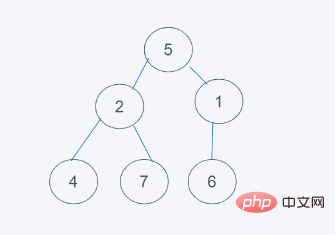
3.发现元素6大于堆顶元素5，弹出堆顶元素5，由堆尾元素6替换
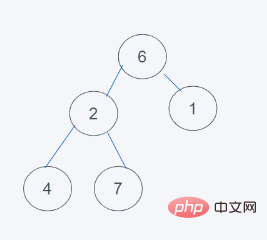
4.依据python的最小堆特性，元素6>元素1且元素6>元素2，但元素2>元素1， 交换6与1
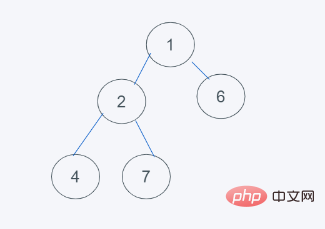
5.符合要求，则结果为[1, 2, 6, 4, 7]
由结果可以看出，当插入元素小于堆顶元素时，则堆不会发生改变，当插入元素大于堆顶元素时，则堆依据python堆的最小堆特性处理。
将列表转换为堆。
h = [1, 2, 3, 5, 7] heapq.heapify(h) print(h) h = [5, 2, 1, 4, 7] heapq.heapify(h) print(h) #输出 [1, 2, 3, 5, 7] [1, 2, 5, 4, 7]
会自动将列表依据python最小堆特性进行重新排列。
弹出并返回最小的元素，并且添加一个新元素item，这个单步骤操作比heappop()加heappush() 更高效。适用于堆元素数量固定的情况。
返回的值可能会比添加的 item 更大。 如果不希望如此，可考虑改用heappushpop()。 它的 push/pop 组合会返回两个值中较小的一个，将较大的值留在堆中。
import heapq h = [1, 2, 3, 5, 7] heapq.heapreplace(h, 6) print(h) h = [5, 2, 1, 4, 7] heapq.heapreplace(h, 6) print(h) #输出 [2, 5, 3, 6, 7] [1, 2, 6, 4, 7]
原有数据是堆
对于插入元素6的操作过程如下：
1.初始状态
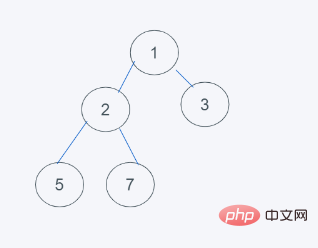
2.弹出最小元素，只能弹出堆顶或者堆尾的元素，很明显，最小元素是1，弹出1，插入元素是6，代替堆顶元素
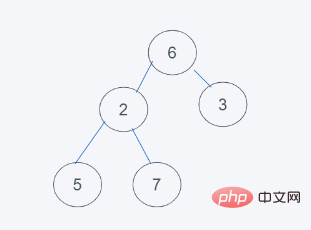
3.依据python堆的最小堆特性，6>2,交换6与2
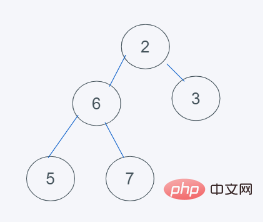
4.依据python堆的最小堆特性，6>5,交换6与5
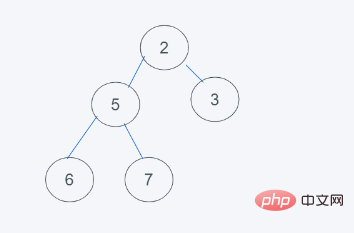
5.符合要求，则结果为[2, 5, 3, 6 ,7]
原有数据不是堆
对于插入元素6的操作过程如下：
1.初始状态
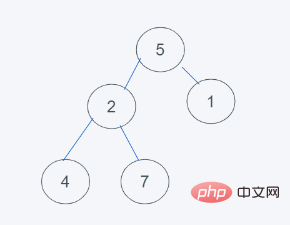
2.对于数据不为堆的情况下，默认移除第一个元素，这里就是元素5，然后插入元素6到堆顶
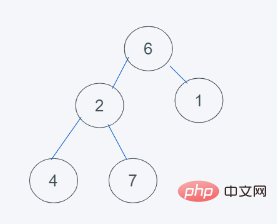
3.依据python的最小堆特性，元素6>1,交换元素6与1
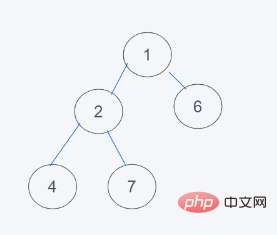
4.符合要求，即结果为[1, 2, 6, 4, 7
将多个已排序的输入合并为一个已排序的输出（例如，合并来自多个日志文件的带时间戳的条目）。 返回已排序值的 iterator。注意需要是已排序完成的可迭代对象（默认为从小到大排序），当reverse为True时，则为从大到小排序。
从 iterable 所定义的数据集中返回前 n 个最大元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。
等价于: sorted(iterable, key=key, reverse=True)[:n]。
import time
import heapq
h = [1, 2, 3, 5, 7]
size = 1000000
start = time.time()
print(heapq.nlargest(3, h))
for i in range(size):
heapq.nlargest(3, h)
print(time.time() - start)
start = time.time()
print(sorted(h, reverse=True)[:3:])
for i in range(size):
sorted(h, reverse=True)[:3:]
print(time.time() - start)
#输出
[7, 5, 3]
1.6576552391052246
[7, 5, 3]
0.2772986888885498
[7, 5, 4]由上述结构可见，heapq.nlargest与sorted(iterable, key=key, reverse=False)[:n]功能是类似的，但是性能方面还是sorted较为快速。
从 iterable 所定义的数据集中返回前 n 个最小元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。 等价于: sorted(iterable, key=key)[:n]。
import time
import heapq
h = [1, 2, 3, 5, 7]
size = 1000000
start = time.time()
print(heapq.nsmallest(3, h))
for i in range(size):
heapq.nsmallest(2, h)
print(time.time() - start)
start = time.time()
print(sorted(h, reverse=False)[:3:])
for i in range(size):
sorted(h, reverse=False)[:2:]
print(time.time() - start)
#输出
[1, 2, 3]
1.1738648414611816
[1, 2, 3]
0.2871997356414795由上述结果可见，sorted的性能比后面两个函数都要好，但如果只是返回最大的或者最小的一个元素，则使用max和min最好。
由于在python中堆的特性是最小堆，堆顶的元素始终是最小的，可以将序列转换成堆之后，再使用pop弹出堆顶元素来实现从小到大排序。具体实现如下：
from heapq import heappush, heappop, heapify
def heapsort(iterable):
h = []
for value in iterable:
heappush(h, value)
return [heappop(h) for i in range(len(h))]
def heapsort2(iterable):
heapify(iterable)
return [heappop(iterable) for i in range(len(iterable))]
data = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
print(heapsort(data))
print(heapsort2(data))
#输出
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]from heapq import heappush, heappop h = [] heappush(h, (5, 'write code')) heappush(h, (7, 'release product')) heappush(h, (1, 'write spec')) heappush(h, (3, 'create tests')) print(h) print(heappop(h)) [(1, 'write spec'), (3, 'create tests'), (5, 'write code'), (7, 'release product')] (1, 'write spec')
上述操作流程如下：
1.当进行第一次push(5, ‘write code’)时
2.当进行第二次push(7, ‘release product’)时，符合堆的要求
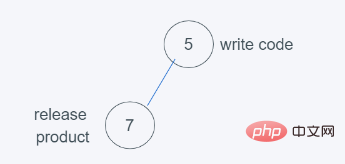
3.当进行第三次push(1, ‘write spec’)时，
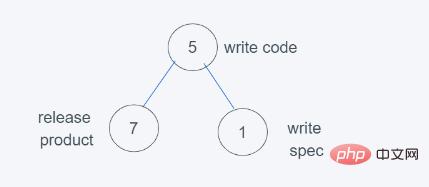
4.依据python的堆的最小堆特性，5>1 ，交换5和1
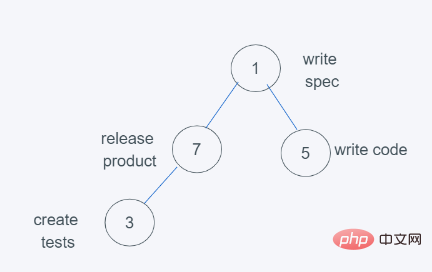
5.当进行最后依次push(3, ‘create tests’)时
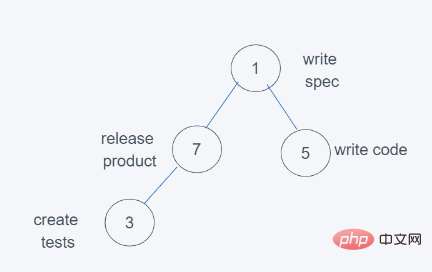
6.依据python堆的最小堆特性，7>3，交换7与3
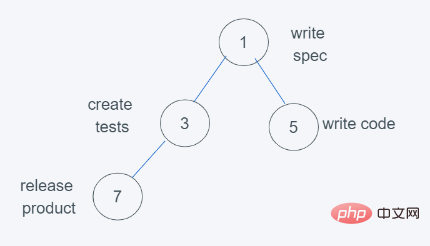
7.符合要求，因此结果为[(1, ‘write spec’), (3, ‘create tests’), (5, ‘write code’), (7, ‘release product’)],弹出元素则是堆顶元素，数字越小，优先级越大。
Das obige ist der detaillierte Inhalt vonSo implementieren Sie den in Python integrierten Heap. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
