
Der Sortieralgorithmus dient zur Faktorisierung einer oder mehrerer Gruppen der Daten werden nach einem definierten Muster neu geordnet. Die Schlusssequenz wird nach bestimmten Regeln präsentiert.
Bei Sortieralgorithmen sind Stabilität und Effizienz Themen, die wir oft berücksichtigen müssen.
Stabilität: Stabilität bedeutet, dass sich die relative Position der beiden vor und nach der Sortierung nach einem bestimmten Sortieralgorithmus nicht ändert, wenn zwei identische Elemente gleichzeitig in einer Sequenz erscheinen.
Komplexitätsanalyse:
(1) Zeitkomplexität: vom Anfangszustand der Sequenz bis zum endgültigen Sortierergebnis nach Operationen wie Transformation und Verschiebung des Sortieralgorithmus Ein Maß der Zeit, die für den Prozess eines Staates aufgewendet wird.
(2) Raumkomplexität: Dies ist der Raumaufwand, der vom Anfangszustand der Sequenz über den Prozess der Sortierung und Verschiebungstransformation bis zum Endzustand aufgewendet wird.
Übliche Sortieralgorithmen werden in die folgenden Typen unterteilt:
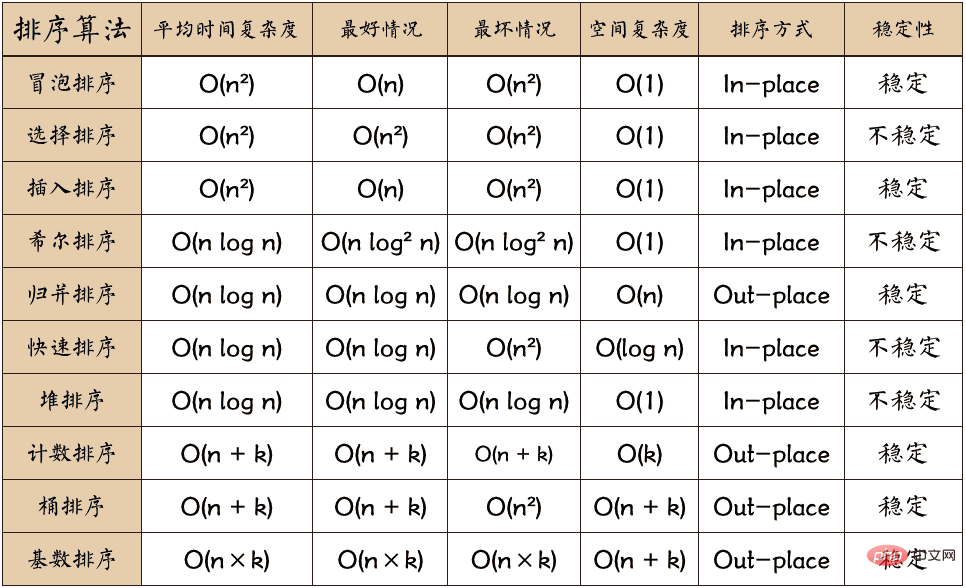
Binary Insertion Sort ist eine Verbesserung des Einfügungssortierungsalgorithmus. Fügen Sie fortlaufend Elemente in die zuvor sortierte Reihenfolge ein. Da die erste Hälfte eine sortierte Sequenz ist, müssen wir nicht nach dem Einfügepunkt suchen. Wir können die Halbsuchmethode verwenden, um die Suche nach dem Einfügepunkt zu beschleunigen.
Setzen Sie beim Einfügen eines neuen Elements in das sortierte Array bei der Suche nach dem Einfügepunkt das erste Element des einzufügenden Bereichs auf a [low], das letzte Element wird auf a[high] gesetzt, dann wird in jeder Vergleichsrunde das einzufügende Element mit a[m] verglichen, wobei m = (low+high)/2, wenn es kleiner ist Als Referenzelement wählen Sie a[low] bis a[m-1] als neuen Einfügebereich (d. h. high=m-1), andernfalls wählen Sie a[m+1] bis a[high] als neuen Einfügebereich ( d. h. low=m+1), Dies wird so lange fortgesetzt, bis low
Kurz gesagt: Nutzen Sie die Ordnungseigenschaften der angeordneten Elemente und nutzen Sie die Eigenschaften der Halbsuche, um schnell die einzufügende Position zu finden.
// Binary Insertion Sort method
private static void binaryInsertSort(int[] array){
for(int i = 1; i < array.length; i++){
int temp = array[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < array[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
array[j] = array[j - 1];
}
array[low] = temp;
}
}Der Halbeinfügungs-Sortieralgorithmus ist ein stabiler Sortieralgorithmus, der die Anzahl der Vergleiche zwischen Schlüsselwörtern erheblich reduziert schneller als Der Sortieralgorithmus mit direkter Einfügung ist schnell, aber die Anzahl der Datensatzverschiebungen hat sich nicht geändert, sodass die zeitliche Komplexität des Sortieralgorithmus mit halber Einfügung immer noch O (n ^ 2) beträgt, was mit der des Sortieralgorithmus mit direkter Einfügung identisch ist.
Zeitkomplexität
Bester Fall: O(n). Wenn die Elemente vorwärts sortiert werden, wird die Position direkt am Anfang gefunden, ohne Suchen und Verschieben.
Schlimmster Fall: O(n^2). Wenn die Elemente in umgekehrter Reihenfolge sortiert sind, ist jedes Mal eine Datensuche erforderlich.
Durchschnittliche Komplexität: O(n^2).
Raumkomplexität: O(1). Zum Aufzeichnen der wichtigsten Informationseinheiten werden nur wenige Speicherplätze benötigt, d. h. die Speicherplatzkomplexität beträgt O(1).
Beispiel:
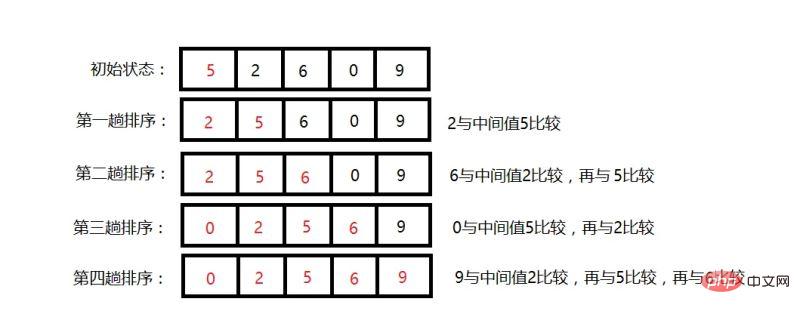
Die Gesamtidee des Algorithmus war Wie oben beschrieben, verwenden wir ein Beispiel direkt, um das Wasser zu testen.
halbierte Einfügungssortierung
Problembeschreibung:
Sie erhalten eine Ganzzahl-Array-Nummer, bitte sortieren Sie das Array in aufsteigender Reihenfolge.
Beispiel 1:
Eingabe: nums = [5,2,3,1]
Ausgabe: [1,2,3,5 ]
Beispiel 2:
Eingabe: nums = [5,1,1,2,0,0]
Ausgabe: [0, 0,1,1,2,5]
Tipp:
1 <= nums.length <= 5 * 104
- 5 * 104 <= nums[i] <= 5 * 104
class Solution {
public int[] sortArray(int[] nums) {
for(int i = 1; i < nums.length; i++){
int temp = nums[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < nums[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
nums[j] = nums[j - 1];
}
nums[low] = temp;
}
return nums;
}
}Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen Sortieralgorithmus mit halber Einfügung in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




