1. Algorithmuseffizienz
Die Algorithmuseffizienzanalyse ist in zwei Typen unterteilt: Der erste ist die Zeiteffizienz und der zweite ist die Raumeffizienz. Zeiteffizienz wird als Zeitkomplexität bezeichnet, und Raumeffizienz wird als Raumkomplexität bezeichnet. Die Zeitkomplexität misst hauptsächlich die Laufgeschwindigkeit eines Algorithmus, während die Raumkomplexität hauptsächlich den zusätzlichen Speicherplatz misst, den ein Algorithmus benötigt. In den Anfängen der Computerentwicklung war die Speicherkapazität von Computern sehr gering. Daher liegt uns die Komplexität des Weltraums sehr am Herzen. Nach der rasanten Entwicklung der Computerindustrie hat die Speicherkapazität von Computern jedoch ein sehr hohes Niveau erreicht. Daher müssen wir der räumlichen Komplexität eines Algorithmus keine besondere Aufmerksamkeit mehr schenken.
2. Zeitkomplexität
1. Zeitkomplexitätskonzept
Die von einem Algorithmus benötigte Zeit ist proportional zur Anzahl der Ausführungen seiner Anweisungen. Die Anzahl der Ausführungen grundlegender Operationen in einem Algorithmus ist die zeitliche Komplexität des Algorithmus. Das heißt, wenn wir einen Code erhalten und die zeitliche Komplexität des Codes betrachten, finden wir hauptsächlich heraus, wie oft der Code mit den meisten ausgeführten Anweisungen im Code ausgeführt wurde.
2. Asymptotische Darstellung von Big O
Sehen Sie sich die Bildanalyse an:
Wenn N Die Werte werden immer größer und die Werte von 2N und 10 können ignoriert werden.
Tatsächlich müssen wir bei der Berechnung der Zeitkomplexität nicht die genaue Anzahl der Ausführungen berechnen, sondern nur die ungefähre Anzahl der Ausführungen. Daher verwenden wir hier die asymptotische Darstellung von Big O.
Big-O-Notation: Es handelt sich um ein mathematisches Symbol, das zur Beschreibung des asymptotischen Verhaltens einer Funktion verwendet wird.
1. Ersetzen Sie alle additiven Konstanten zur Laufzeit durch die Konstante 1.
2. In der modifizierten Laufzeitfunktion wird nur der Term höchster Ordnung beibehalten.
3. Wenn der Term höchster Ordnung existiert und nicht 1 ist, entfernen Sie die Konstante multipliziert mit diesem Term. Das Ergebnis ist die Big-O-Ordnung.
Durch das Obige werden wir feststellen, dass die asymptotische Darstellung von Big O diejenigen Elemente entfernt, die wenig Einfluss auf die Ergebnisse haben, und die Anzahl der Ausführungen ausdrückt prägnant und klar.
Darüber hinaus gibt es für die Zeitkomplexität einiger Algorithmen beste, durchschnittliche und schlechteste Fälle:
Worst Case: die maximale Anzahl von Läufen (Obergrenze) für jede Eingabegröße# 🎜 🎜#
Durchschnittsfall: die erwartete Anzahl von Läufen für jede Eingabegröße
Bestfall: die minimale Anzahl von Läufen (Untergrenze) für jede Eingabegröße
#🎜🎜 #Beispiel: Bei einer Suche nach Daten Algorithmus, sodass die zeitliche Komplexität der Suche nach Daten im Array O(N) ist 🎜#
Die Grundoperation wird 2N+10 Mal ausgeführt. Durch Ableitung der großen O-Ordnungsmethode ist bekannt, dass die Zeitkomplexität O(N)
Beispiel 2 ist.
Die Grundoperation wird M+N-mal ausgeführt, und es gibt zwei unbekannte Zahlen M und N, und die Zeitkomplexität ist O(N). +M)
Beispiel 3:
Grundoperationsausführung 100 Mal, durch Ableitung der großen O-Order-Methode, der Zeit Komplexität ist O(1)
Beispiel 4: Berechnen Sie die zeitliche Komplexität der Blasensortierung
Die Grundoperation wird N ausgeführt Bestenfalls mal (N*(N-1))/2 Mal, wenn man die Methode der großen O-Reihenfolge + Zeitkomplexität ableitet, wird im Allgemeinen der schlimmste Fall gesehen, und die Zeit ist komplex ^2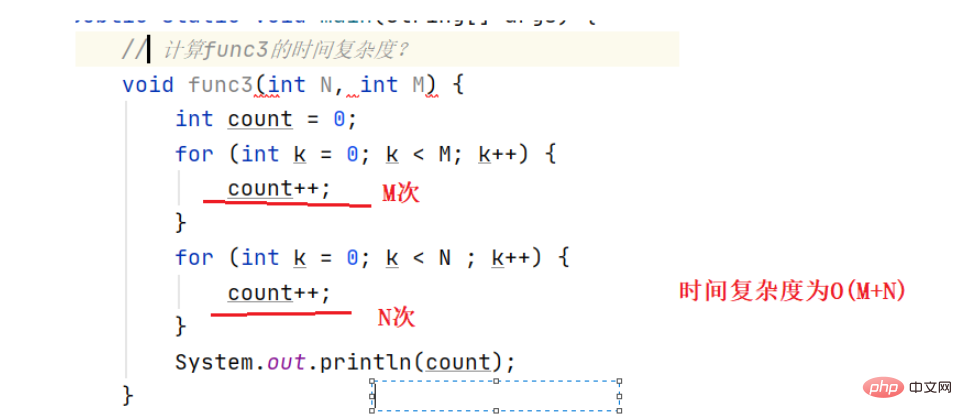
Beispiel 5: Zeitkomplexität der binären Suche
Grundoperationen führen 1 mal am besten aus, das schlechteste ist O( logN) mal beträgt die Zeitkomplexität O(logN) ps: logN bedeutet, dass die Basis 2 und der Logarithmus an einigen Stellen N ist (es wird empfohlen, dies durch Origami-Suche zu erklären. Wie wird logN berechnet?) (Weil binäre Suche Eliminiert jedes Mal die Hälfte der ungeeigneten Werte, die verbleibenden Werte nach einer binären Suche sind: n/2 und die verbleibenden Werte nach zwei binären Suchen sind: n/2/2 = n/4)#🎜 🎜## 🎜🎜#Beispiel 6: Berechnen Sie die zeitliche Komplexität der faktoriellen Rekursion
Die zeitliche Komplexität der Rekursion = die Anzahl der Rekursionen * die Häufigkeit, mit der jede Rekursion ausgeführt wird
#🎜🎜 #
# 🎜🎜#
Durch Berechnung und Analyse wird festgestellt, dass die Grundoperation N-mal rekursiv ist und die Zeitkomplexität O(N) ist
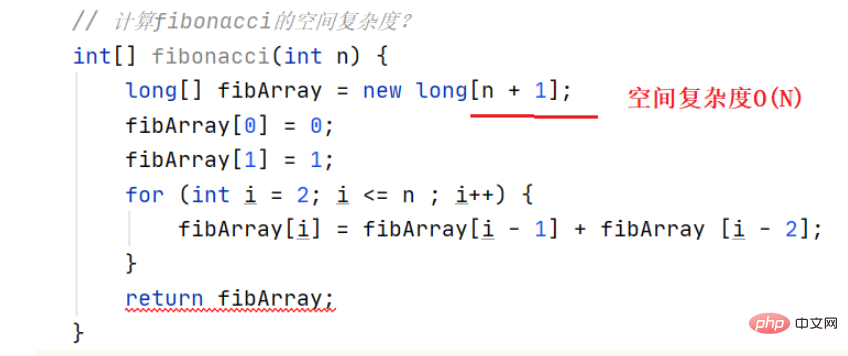
Beispiel 7: Berechnen die zeitliche Komplexität der Fibonacci-Rekursion#🎜 🎜#
Durch Berechnung und Analyse wurde festgestellt, dass die Grundoperation 2^N-mal rekursiv ist und die Zeitkomplexität O(2^N) beträgt.
Regel:
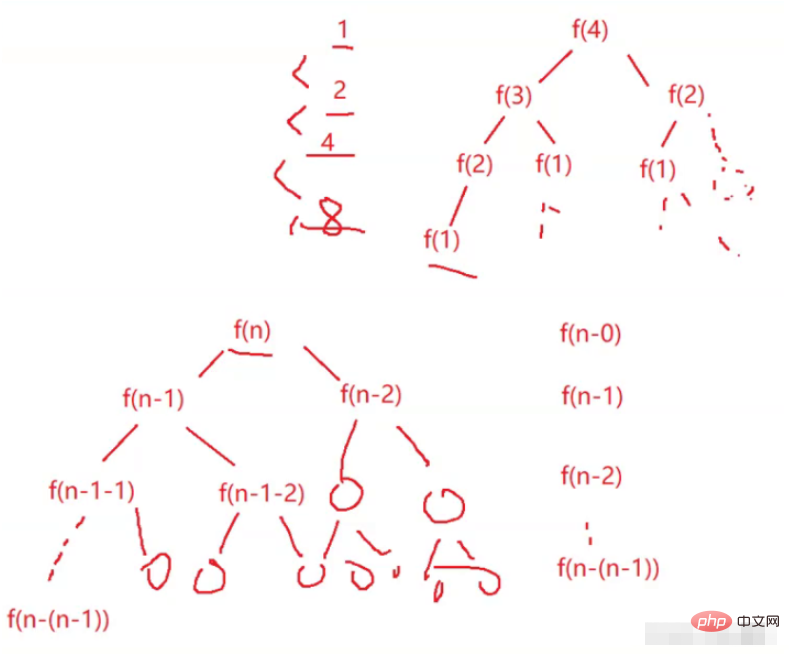
2^0+2^1+2^2+2^3……2^ (n-(n-1))
Summe der geometrischen Folge
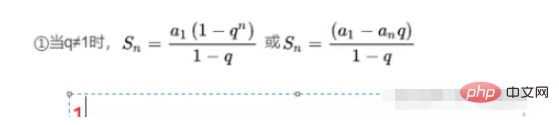
a1 stellt den ersten Term dar, q Das Verhältnis ist 2, 1(1-2^n)/-1, was 2^n+1 entspricht, also ist die Zeitkomplexität O(2^n)
3. Raumkomplexität #🎜 🎜#
Die Speicherplatzkomplexität ist ein Maß für die Menge an Speicherplatz, die ein Algorithmus während des Betriebs vorübergehend belegt. Die Speicherplatzkomplexität gibt nicht an, wie viele Bytes Speicherplatz das Programm einnimmt, da dies nicht sehr aussagekräftig ist. Daher wird die Speicherplatzkomplexität anhand der Anzahl der Variablen berechnet. Die Regeln zur Berechnung der Raumkomplexität ähneln im Wesentlichen der praktischen Komplexität, und es wird auch die asymptotische Big-O-Notation verwendet.
Beispiel 1: Berechnen Sie die Raumkomplexität der Blasensortierung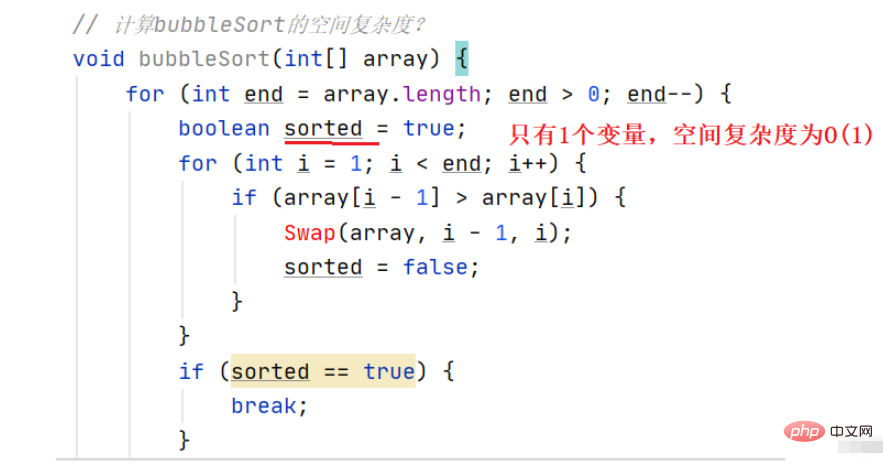
verwendet einen konstanten zusätzlichen Raum, also die Raumkomplexität Es ist O(1) Raum, die Raumkomplexität ist O(N)
Beispiel 3: Berechnen Sie die Raumkomplexität der faktoriellen Rekursion
#🎜 🎜# N-maliger rekursiver Aufruf, N Stapelrahmen werden geöffnet und jeder Stapelrahmen belegt eine konstante Menge an Speicherplatz. Die Raumkomplexität ist O(N)
Das obige ist der detaillierte Inhalt vonBeispielanalyse für Java-Zeitkomplexität und Raumkomplexität. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
