In unserem heutigen Leben gehören zu Beispielen für Diagramme soziale Netzwerke wie Twitter, Mastodon und alle Zitiernetzwerke, die Artikel und Autoren, Moleküle, Wissensdiagramme wie UML-Diagramme, Enzyklopädien und Websites mit Hyperlinks und Darstellungen von Sätzen bis verknüpfen Wenn man syntaktische Bäume zu jedem 3D-Gitter hinzufügt, kann man sagen, dass es überall Diagramme gibt.
Kürzlich stellte die Forschungswissenschaftlerin von Hugging Face, Clémentine Fourrier, das heute allgegenwärtige maschinelle Lernen von Graphen im Artikel „Einführung in das maschinelle Lernen von Graphen“ vor. Was sind Grafiken? Warum Diagramme verwenden? Wie lässt sich ein Diagramm am besten darstellen? Wie lernen Menschen aus Grafiken? Clémentine Fourrier wies darauf hin, dass ein Diagramm eine Beschreibung von Elementen ist, die durch Beziehungen miteinander verbunden sind. Von präneuronalen Methoden bis hin zu grafischen neuronalen Netzen handelt es sich dabei immer noch um häufig verwendete Methoden zum Lernen von Diagrammen.
Darüber hinaus haben einige Forscher kürzlich damit begonnen, über die Anwendung von Transformern auf Diagramme nachzudenken. Transformer haben eine gute Skalierbarkeit und können einige der Einschränkungen von GNN mildern, und die Aussichten sind sehr vielversprechend.
Im Wesentlichen ist das Diagramm eine Beschreibung der durch die Beziehung verbundenen Elemente. Elemente eines Graphen (oder Netzwerks) werden Knoten (oder Eckpunkte) genannt und sind durch Kanten (oder Links) verbunden. In einem sozialen Netzwerk sind beispielsweise Knoten Benutzer und Kanten Verbindungen zwischen Benutzern in Molekülen, Knoten sind Atome und Kanten sind ihre molekularen Bindungen.
Wie Sie sehen, müssen Sie bei der Verwendung von Daten zunächst deren optimale Darstellung berücksichtigen, einschließlich homogener/heterogener , gerichtet/ungerichtet usw. ... Zeitentwicklung, die in der Physik verwendet werden kann, um die Entwicklung eines Systems vorherzusagen
Vorhersage-, Klassifizierungs- oder Regressionsaufgaben auf Diagrammebene aus Diagrammen, wie z. B. die Vorhersage der Toxizität von Molekülen
Wenn es darum geht, die Entwicklung eines bestimmten Diagramms vorherzusagen, kann alles im Transformations-Setup, einschließlich Training, Validierung und Tests, im selben Diagramm durchgeführt werden. Das Erstellen von Trainings-, Bewertungs- oder Testdatensätzen aus einem einzigen Diagramm ist jedoch nicht einfach, und viel Arbeit wird mithilfe verschiedener Diagramme (getrennte Trainings-/Bewertungs-/Testaufteilungen) erledigt, was als Induktionseinstellung bezeichnet wird.
Es gibt zwei gängige Möglichkeiten, Graphverarbeitungen und -operationen darzustellen, entweder als Menge aller Kanten (möglicherweise ergänzt durch eine Menge aller Knoten) oder als Adjazenzmatrix zwischen allen Knoten. Unter diesen ist die Adjazenzmatrix eine quadratische Matrix (Knotengröße × Knotengröße), die angibt, welche Knoten direkt mit anderen Knoten verbunden sind. Beachten Sie, dass eine dünn besetzte Adjazenzmatrix die Berechnung erschwert, da die meisten Graphen nicht dicht verbunden sind.
Grafiken unterscheiden sich stark von typischen Objekten, die in ML verwendet werden, aufgrund ihrer komplexeren Topologie als „Sequenzen“ (wie Text und Audio) oder „geordnete Gitter“ (wie Bilder und Videos): auch wenn sie als Liste dargestellt werden können oder Matrix, aber diese Darstellung kann nicht als geordnetes Objekt betrachtet werden. Das heißt, wenn Sie die Wörter in einem Satz verschlüsseln, erstellen Sie einen neuen Satz, und wenn Sie ein Bild verschlüsseln und seine Spalten neu anordnen, erstellen Sie ein neues Bild.
Illustration: Das Hugging Face-Logo und das unterbrochene Hugging Face-Logo sind völlig unterschiedliche neue Bilder
Aber das ist bei der Figur nicht der Fall: wenn wir die Kantenliste der Figur auswaschen oder Spalten der Adjazenzmatrix, es ist immer noch derselbe Graph.
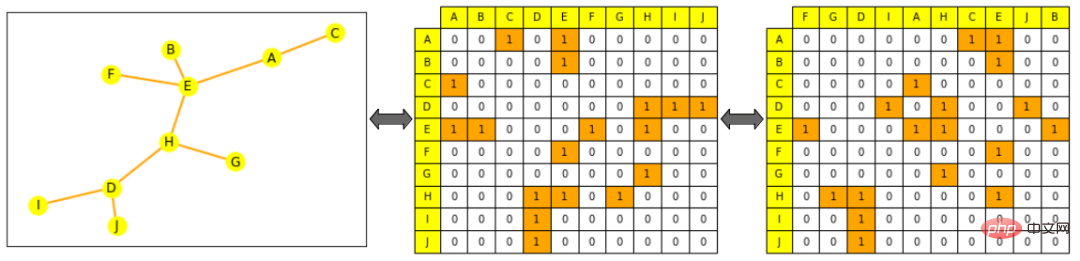
Bildhinweis: Das linke ist ein kleines Bild, Gelb stellt Knoten dar, Orange stellt die Kanten im mittleren Bild dar, die Spalten und Zeilen sind in alphabetischer Reihenfolge der Knoten angeordnet: die Zeile von Knoten A (erste Zeile) Sie können sehen, dass es mit E und C verbunden ist. Das Bild rechts stört die Adjazenzmatrix (die Spalten sind nicht mehr in alphabetischer Reihenfolge), was immer noch eine gültige Darstellung des Diagramms ist, also A ist immer noch mit E und C verbunden Das vollständige Diagramm hängt von den spezifischen Aufgabenanforderungen ab und trainiert einen Prädiktor für die Zielaufgabe. Wie bei anderen Mustern können Sie die mathematische Darstellung eines Objekts so einschränken, dass es einem ähnlichen Objekt mathematisch nahe kommt. Allerdings lässt sich Ähnlichkeit im Graphen ML nur schwer genau definieren: Sind beispielsweise zwei Knoten ähnlicher, wenn sie die gleiche Bezeichnung oder die gleichen Nachbarn haben?
Präneurale Methoden
Einfach technische Features nutzen
Funktionen auf Knotenebene können Informationen zur Wichtigkeit sowie strukturbasierte Informationen bereitstellen und diese kombinieren.
Knotenzentralität kann verwendet werden, um die Wichtigkeit von Knoten im Diagramm zu messen. Sie wird rekursiv berechnet, indem die Nachbarzentralitäten jedes Knotens bis zur Konvergenz summiert werden, oder rekursiv, indem der kürzeste Abstand zwischen Knoten gemessen wird. Der Knotengrad ist seine Zahl Anzahl der direkten Nachbarn; der Clustering-Koeffizient misst, wie viele verschiedene Graphlets an einem bestimmten Knoten verwurzelt sind, wobei alle Minifiguren verwendet werden können.
Hinweis zur Abbildung: Kleines Diagramm mit 2 bis 5 Knoten
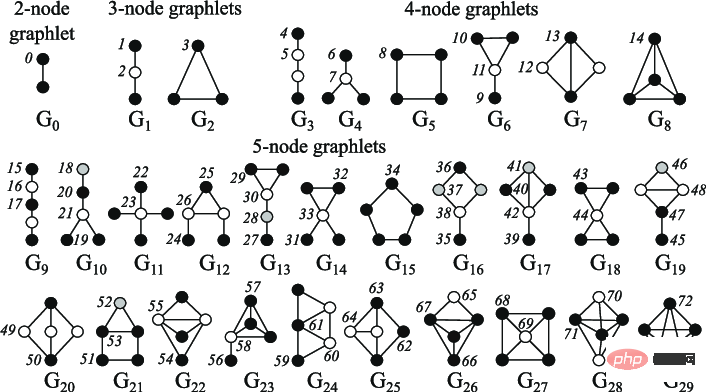Features auf Kantenebene werden durch detailliertere Informationen zur Knotenkonnektivität ergänzt, einschließlich der kürzesten Entfernung zwischen zwei Knoten, ihren gemeinsamen Nachbarn und dem Katz Index (die Anzahl der möglichen Pfade einer bestimmten Länge zwischen zwei Knoten – die direkt aus der Adjazenzmatrix berechnet werden können).
Funktionen auf Diagrammebene enthalten allgemeine Informationen über die Ähnlichkeit und Unterscheidbarkeit von Diagrammen, wobei die Anzahl der Untergraphen zwar rechenintensiv ist, aber Informationen über die Formen von Untergraphen liefert. Die Kernmethode misst die Ähnlichkeit zwischen Diagrammen mithilfe verschiedener „Bag-of-Nodes“-Methoden (ähnlich Bag-of-Words).
Laufbasierte Methoden verwenden die Wahrscheinlichkeit, Knoten j von Knoten i in einem Zufallsgang zu besuchen, um das Ähnlichkeitsmaß zu definieren. Diese Methoden kombinieren lokale und globale Informationen. Beispielsweise simulierte Node2Vec zuvor zufällige Spaziergänge zwischen Diagrammknoten und verwendete Skip-Grams, um diese Spaziergänge zu verarbeiten, genau wie wir Wörter in Sätzen verwenden, um Einbettungen zu berechnen.
Diese Methoden können auch verwendet werden, um die Berechnung der PageRank-Methode zu beschleunigen, die jedem Knoten einen Wichtigkeitswert basierend auf seinen Verbindungen zu anderen Knoten zuweist, z. B. durch Zufallswanderungen, um seine Zugriffshäufigkeit zu bewerten. Die oben genannten Methoden weisen jedoch auch bestimmte Einschränkungen auf. Sie können keine neuen Knoten einbetten, die strukturelle Ähnlichkeit zwischen Knoten nicht gut erfassen und keine zusätzlichen Funktionen verwenden.
Neuronale Netze können auf unsichtbare Daten verallgemeinern. Wie sollte ein gutes neuronales Netzwerk angesichts der zuvor erwähnten Darstellungsbeschränkungen mit Diagrammen umgehen?
Zwei Methoden werden unten gezeigt:
Gleichung: P(f(G))=f(P(G))P(f(G))=f(P(G)), wobei f das Netzwerk und P die Permutation ist Funktion und G ist der Graph. Daher wurde eine neue Architektur eingeführt: Graphische neuronale Netze (zunächst als zustandsbasierte Maschine).
Aggregation und Messaging
Es gibt viele Möglichkeiten, Informationen von Knotennachbarn zu aggregieren, z. B. Summierung und Mittelung. Zu den früheren ähnlichen Clustering-Methoden gehören:
Graph Convolutional Networks, für Knotennachbarn Mittelung der normalisierten Darstellung von Sampling-Nachbarn bei verschiedenen Hops;
Wählen Sie eine Aggregation: Einige Aggregationstechniken (insbesondere Mittelwert-/Maximalmengen) leiden unter Fehlern bei der Erstellung feinkörniger Darstellungen, die zwischen verschiedenen Knotennachbardarstellungen ähnlicher Knoten unterscheiden. Bei Mittelwertmengen hat man beispielsweise die Nachbarn von 4 Knoten werden als 1, 1, -1 und -1 dargestellt, und der Durchschnitt ist 0, was sich nicht von einem Nachbarn unterscheidet, bei dem nur 3 Knoten als -1, 0 und 1 dargestellt werden.
Auf jeder neuen Ebene umfasst die Knotendarstellung immer mehr Knoten. Ein Knoten durchläuft die erste Schicht, eine Ansammlung seiner direkten Nachbarn. Bis zur zweiten Schicht ist es immer noch eine Ansammlung seiner unmittelbaren Nachbarn, aber seine Darstellung umfasst jetzt auch deren eigene Nachbarn (aus der ersten Schicht). Nach n Ebenen wird die Darstellung aller Knoten zur Menge aller ihrer Nachbarn im Abstand n und daher zu einer Aggregation des gesamten Graphen, wenn sein Durchmesser kleiner als n ist.
Wenn zu viele Netzwerkschichten vorhanden sind, besteht die Gefahr, dass jeder Knoten zu einer Aggregation des gesamten Diagramms wird (und die Knotendarstellung für alle zur gleichen Darstellung konvergiert). Knoten), das sogenannte Überglättungsproblem, kann gelöst werden durch: Skalieren des GNN auf eine ausreichend kleine Anzahl von Schichten, sodass jeder Knoten als das gesamte Netzwerk angenähert wird (indem zunächst der Durchmesser und die Form des Diagramms analysiert werden) 🎜 #Nicht-Messaging-Ebene zum Verarbeiten von Nachrichten hinzufügen (z. B. einfaches MLP)
GRPE: Relative Positionskodierung für Graph Transformer, stellt den Graph Relative Position Encoding Transformer vor, der Positionskodierung und Knoteninformationen auf Diagrammebene, Positionskodierung auf Kantenebene und kombiniert Knoteninformationen werden kombiniert und die beiden werden sorgfältig kombiniert, um das Diagramm darzustellen.
Do Transformers Really Badled for Graph Representation stellt Microsofts Graphormer vor, der bei seiner Veröffentlichung auf der OGB den ersten Platz belegte. Die Architektur verwendet Knotenmerkmale als Abfragen/Schlüssel/Werte in der Aufmerksamkeit und kombiniert ihre Darstellung mit Zentralität, räumlicher Kodierung und Kantenkodierung im Aufmerksamkeitsmechanismus.
Neueste Forschung „Reine Transformatoren sind leistungsstarke Graph-Lernende“ führte TokenGT in die Methode ein, die den Eingabegraphen als eine Reihe von Knoten- und Kanteneinbettungen darstellt Das heißt, die Erweiterung mit orthogonalen Knotenbezeichnern und trainierbaren Typbezeichnern ohne Positionseinbettungen und die Einspeisung dieser Sequenz als Eingabe in Transformer ist sehr einfach und gleichzeitig sehr effektiv.
Papieradresse: https://arxiv.org/abs/2205.12454
Die Verwendung von Transformern für Diagramme steckt noch weitgehend in den Kinderschuhen, aber im Moment sind die Aussichten vielversprechend. Sie können einige der Einschränkungen von GNNs, wie z. B. die Skalierung auf größere oder größere dichte Diagramme, mildern oder steigern Modellgröße ohne Überglättung.
Das obige ist der detaillierte Inhalt vonMaschinelles Lernen von Graphen ist überall und nutzt Transformer, um GNN-Einschränkungen zu mildern. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
