
Titel. Beschreibung
#🎜🎜 # Bei einem gegebenen Array mit n ganzen Zahlen besteht Ihre Aufgabe darin, zu prüfen, ob es durch Ändern von höchstens einem Element nicht absteigend werden kann. Ein nicht absteigendes Array erfüllt array[i-1]Beispiel 1:
ⅰ Eingabe: [4,2,3]ⅱ Ausgabe: True # 🎜🎜#ⅲ Hinweis: Sie können die erste Zahl 4 in 1 ändern, um [1,2,3] als nicht absteigendes Array zu erhalten
Beispiel 2: # 🎜🎜#ⅰ Eingabe: [4,2,1]
ⅱ Ausgabe: Falschⅲ Beschreibung: Höchstens eine Änderung ist nicht möglich -Element bewirkt, dass das Array nicht absteigend ist. Analyse von Problemlösungsideen a. Einfaches Denken Kann erhalten werden, es gibt nichts mehr als drei Situationen: diejenigen, die die Bedingungen ohne Änderung erfüllen, diejenigen, die die Bedingungen erfüllen können, indem sie ein Element ändern, und diejenigen, die die Bedingungen nicht erfüllen können, selbst wenn ein Element geändert wird. Durchlaufen Sie im ersten Fall einfach das Array, um zu sehen, ob jedes Element im Array größer oder gleich dem vorherigen Element ist. Wenn ja, geben Sie true zurück. Im zweiten Fall können Sie das zu ändernde Zahlenarray[i] aufzählen und dann prüfen, ob die Zahl vor dem Array[i] nicht abnehmend ist und ob die Zahl nach dem Array[i] nicht abnehmend ist, #🎜 🎜# Abschließend sollten Sie auch prüfen, obarray[i-1] wahr ist (wenn array[ Wenn sich i] an der Grenze befindet, ist keine Überprüfung erforderlich. Wenn dies zutrifft, können Sie array[i] in eine beliebige Zahl zwischen array[i-1] und array[i+1] ändern, um das Array zu einem Nicht-Array zu machen. Absteigendes Array. Dies ist Fall 2. Gibt „true“ zurück, wenn es nicht für alle i wahr ist, dann ist es Fall drei und es wird „false“ zurückgegeben. Die zeitliche Komplexität hierfür beträgt O(n^2) und die zusätzliche räumliche Komplexität beträgt O(1). b. Welche Bedingungen können erfüllt sein, um eine Zahl nach der Änderung in ein nicht abnehmendes Array umzuwandeln? Offensichtlich sollte ein solches Array die Bedingung erfüllen, dass es nur ein Paar benachbarter Zahlen gibt, das die Nicht-Abnahmebedingung nicht erfüllt, das heißt, es gibt nur ein eindeutiges i (1array[i]: Es kann behauptet werden, dass bei mehreren solchen i das ursprüngliche Array nicht zu einem nicht absteigenden Array werden kann, indem höchstens eine Zahl geändert wird. Kann also jedes Array, das diese Bedingung erfüllt, durch Ändern einer Zahl die Nicht-Abnahme erfüllen? Nein, zum Beispiel [2,4,1,3], nur die angrenzenden 4,1 erfüllen nicht die nicht abnehmende Zahl, aber sie können nicht nicht abnehmend werden, indem nur eine Zahl geändert wird. Wenn es tatsächlich nur ein i gibt, das array[i-1]>array[i] erfüllt, muss die zu ändernde Zahl zwischen den beiden Zahlen array[i-1] und array[i] liegen, also Sie kann den vorherigen Ansatz anwenden und die beiden Situationen getrennt beurteilen. Da array[i-1]>array[i] nur für i wahr ist, erfüllen alle anderen benachbarten Zahlen die nicht abnehmende Bedingung, also für array[i-1] Es wird gesagt, dass die Arrays davor und danach erfüllen jeweils die nicht absteigenden Bedingungen, und das Gleiche gilt für Array [i]. Daher müssen Sie nur beurteilen, ob die beiden Arrays davor und danach zu einem nicht absteigenden Array verbunden werden können. Insbesondere wenn die zu ändernde Zahl array[i-1] ist, müssen Sie nur beurteilen, ob array[i-2]array[i], und die Bedingungen für die endgültige Rückgabe von true sind array[i-1], array[i] ist die Grenze oder array[i-2] Referenzprogramm Java-Version:
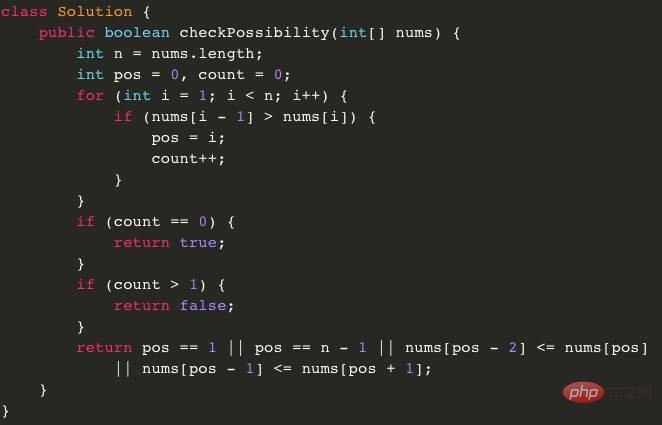
Das obige ist der detaillierte Inhalt vonSo implementieren Sie ein nicht absteigendes Array in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




