So implementieren Sie Graph Traversal in Java

1. Graphendurchquerung

Beginnen Sie bei einem bestimmten Scheitelpunkt im Diagramm und besuchen Sie die verbleibenden Scheitelpunkte im Diagramm. Jeder Scheitelpunkt wird nur einmal besucht.

Es gibt zwei Arten der Diagrammdurchquerung: Tiefendurchquerung (DFS) und Breitendurchquerung Durchquerung BFS

2. Durchquerung der Tiefe

Durchquerung der Tiefe zuerst mit der Tiefe zuerst. Ähnlich wie bei der Vorbestellungsdurchquerung eines Binärbaums

Ideen:

1. Führen Sie eine Tiefendurchquerung ab einem bestimmten Scheitelpunkt durch und markieren Sie den Scheitelpunkt als besucht

2. Wählen Sie einen beliebigen Pfad aus, der vom Scheitelpunkt aus beginnt, und durchlaufen Sie ihn bis zum Ende und Markieren Sie die besuchten Scheitelpunkte

3. Nachdem Sie in Schritt 2 bis zum Ende durchquert haben, kehren Sie zum vorherigen Scheitelpunkt zurück und wiederholen Sie Schritt 2

4. Ende des Durchquerens aller Scheitelpunkte Sie können wissen, dass dies ein rekursiver Prozess ist. Im Grunde ist DFS dasselbe wie Backtracking.

Durchquerung:

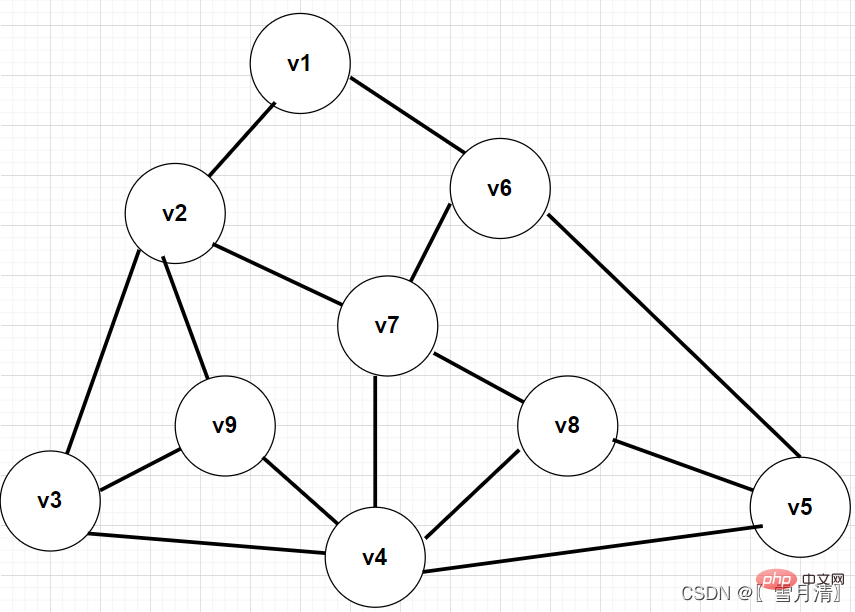Nehmen Sie dieses Bild als Beispiel, um eine Tiefendurchquerung durchzuführen 5

V6

V7

V8

V9

Der Code zum Erstellen des Diagramms:

	static void dfs(int[][] graph,int idx,boolean[]visit) {
		int len = graph.length;
		//访问过
	 if(visit[idx]) return;
	 //访问该顶点
	 System.out.println("V"+idx);
	 //标志顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
	 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
	 //递归进行dfs遍历
		 dfs(graph, i, visit);
		 }
	 }
			
	}

3. Verwenden Sie DFS, um zu bestimmen, ob im gerichteten Diagramm ein Zyklus vorhanden ist.

Idee: Beim Durchqueren eines bestimmten Scheitelpunkts, wenn zusätzlich zum vorherigen Scheitelpunkt , es gibt andere verbundene Scheitelpunkte, die besucht wurden, dann muss es einen Zyklus geben

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit);
		
	}

Hinweis: Es handelt sich um einen gerichteten Graphen, um zu bestimmen, ob ein Zyklus existiert, und ein ungerichteter Graph ist bedeutungslos, um zu bestimmen, ob ein Zyklus existiert, weil der Eckpunkte von zwei beliebigen vorhandenen Pfaden können Zyklen sein

4. Bei der Breitendurchquerung geht es darum, zuerst die Breite (Breite) zu durchqueren. Ähnlich dem Level-Ordnungs-Durchlauf eines Binärbaums

Ideen:

1. Führen Sie einen Breitendurchlauf von einem bestimmten Scheitelpunkt aus durch und markieren Sie den Scheitelpunkt als besucht

2. Besuchen Sie alle Scheitelpunkte, die mit dem Scheitelpunkt verbunden sind nicht besucht, und markieren Sie die besuchten Scheitelpunkte

3. Wiederholen Sie die Schritte 1 und 2, beginnend mit den in Schritt 2 besuchten Scheitelpunkten

4. Verwenden Sie die Warteschlange, um die Durchquerung zu unterstützen, und die Warteschlangenreihenfolge ist das Ergebnis der Breitendurchquerung V2

V6

V3

V7

V9

V5

V4

V8

Code zum Erstellen eines Diagramms

	//默认无环
   static boolean flag = false;
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			
		}
	 //标记数组 true为访问过
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit,1);
		if(flag) 
			System.out.println("有环");
		
	}
	
	static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {
		int len = graph.length;
	
	 System.out.println("V"+idx);
	 //标记顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
		 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
		 if( !visit[i] ) {
		 dfs(graph, i, visit,idx);
		 }
		 else if(idx != i) {
			 flag = true;
		 }
		 }
	 }
	
	 
	}

Das obige ist der detaillierte Inhalt vonSo implementieren Sie Graph Traversal in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!