 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Vergleichszusammenfassung von fünf Deep-Learning-Modellen für die Zeitreihenvorhersage
Vergleichszusammenfassung von fünf Deep-Learning-Modellen für die Zeitreihenvorhersage
Vergleichszusammenfassung von fünf Deep-Learning-Modellen für die Zeitreihenvorhersage
Die Makridakis M-Wettbewerbsserie (bekannt als M4 bzw. M5) fand 2018 bzw. 2020 statt (M6 fand dieses Jahr auch statt). Für diejenigen, die es nicht wissen: Der M-Serien-Wettbewerb kann als Zusammenfassung des aktuellen Zustands des Zeitreihen-Ökosystems betrachtet werden, der empirische und objektive Beweise für die aktuelle Theorie und Praxis der Prognose liefert.
Die Ergebnisse des M4 2018 zeigten, dass reine „ML“-Methoden traditionelle statistische Methoden bei weitem übertrafen, was damals unerwartet war. In M5[1] zwei Jahre später wurde die höchste Punktzahl nur mit „ML“-Methoden erzielt. Und alle Top 50 basieren grundsätzlich auf ML (hauptsächlich Baummodelle). Bei diesem Wettbewerb wurden LightGBM (zur Zeitreihenvorhersage) sowie Amazons Deepar [2] und N-Beats [3] erstmals vorgestellt. Das N-Beats-Modell wurde 2020 veröffentlicht und ist 3 % besser als der M4-Wettbewerbssieger!
Der kürzlich durchgeführte Wettbewerb zur Vorhersage des Beatmungsdrucks hat gezeigt, wie wichtig der Einsatz von Deep-Learning-Methoden zur Bewältigung von Echtzeit-Zeitreihenherausforderungen ist. Ziel des Wettbewerbs ist es, den zeitlichen Druckverlauf innerhalb einer mechanischen Lunge vorherzusagen. Jede Trainingsinstanz ist eine eigene Zeitreihe, daher handelt es sich bei der Aufgabe um ein Problem mit mehreren Zeitreihen. Das Gewinnerteam reichte eine mehrschichtige, tiefe Architektur ein, die ein LSTM-Netzwerk und einen Transformer-Block umfasste.
In den letzten Jahren wurden viele berühmte Architekturen veröffentlicht, wie zum Beispiel MQRNN und DSSM. Alle diese Modelle tragen viele neue Dinge zum Bereich der Zeitreihenvorhersage mithilfe von Deep Learning bei. Neben dem Gewinn von Kaggle-Wettbewerben brachte es uns auch weitere Fortschritte wie:
- Vielseitigkeit: die Möglichkeit, das Modell für verschiedene Aufgaben zu verwenden.
- MLOP: Die Fähigkeit, Modelle in der Produktion zu verwenden.
- Interpretierbarkeit und Interpretierbarkeit: Black-Box-Modelle sind nicht so beliebt.
In diesem Artikel werden 5 Deep-Learning-Architekturen besprochen, die sich auf die Vorhersage von Zeitreihen spezialisiert haben. Der Artikel lautet:
- N-BEATS(ElementAI)
- DeepAR(Amazon)
- Spacetimeformer[4]
- Temporal Fusion Transformer oder TFT ( Google)[5]
- TSFormer (MAE in Time Series)[7]
N-BEATS
Dieses Muster stammt direkt von der (leider) kurzlebigen Firma ElementAI, die von Yoshua Bengio mitbegründet wurde. Die Top-Level-Architektur und ihre Hauptkomponenten sind in Abbildung 1 dargestellt:
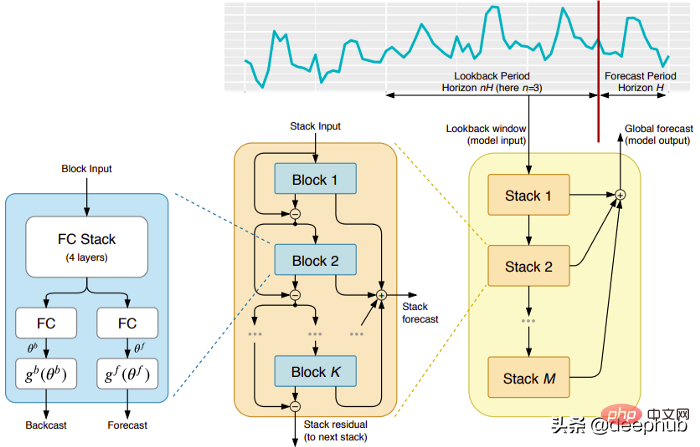
N-BEATS ist eine reine Deep-Learning-Architektur, die auf einem tiefen Stapel integrierter Feed-Forward-Netzwerke basiert, die auch durch Vorwärts- und Rückwärtsverbindungen miteinander verbunden sind .
Jeder Block modelliert nur den Restfehler, der durch den vorherigen Backcast erzeugt wurde, und aktualisiert dann die Vorhersage basierend auf diesem Fehler. Dieser Prozess simuliert die Box-Jenkins-Methode beim Anpassen eines ARIMA-Modells.
Das Folgende sind die Hauptvorteile dieses Modells:
Ausdrucksstark und einfach zu verwenden: Das Modell ist leicht zu verstehen, hat eine modulare Struktur, ist so konzipiert, dass es nur minimales Zeitreihen-Feature-Engineering erfordert und erfordert keine Skalierung der Eingabe .
Das Modell kann über mehrere Zeitreihen hinweg verallgemeinert werden. Mit anderen Worten: Als Eingabe können unterschiedliche Zeitreihen mit leicht unterschiedlichen Verteilungen verwendet werden. In N-BEATS wird es durch Meta-Learning implementiert. Der Meta-Lernprozess umfasst zwei Prozesse: den internen Lernprozess und den externen Lernprozess. Der interne Lernprozess findet innerhalb des Blocks statt und hilft dem Modell, lokale zeitliche Merkmale zu erfassen. Der externe Lernprozess erfolgt in Stapelschichten und hilft dem Modell, globale Merkmale aller Zeitreihen zu lernen.
Doppelte Reststapelung: Die Idee der Restverbindung und -stapelung ist sehr clever und wird in fast allen Arten von tiefen neuronalen Netzwerken verwendet. Das gleiche Prinzip wird bei der Implementierung von N-BEATS angewendet, jedoch mit einigen zusätzlichen Modifikationen: Jeder Block verfügt über zwei Restzweige, von denen einer im Lookback-Fenster läuft (Backcast genannt) und der andere im Vorhersagefenster läuft (Prognose genannt).
Jeder aufeinanderfolgende Block modelliert nur das Residuum, das sich aus dem rekonstruierten Backcast des vorherigen Blocks ergibt, und aktualisiert dann die Vorhersage basierend auf diesem Fehler. Dies hilft dem Modell, das nützliche Backcast-Signal besser anzunähern, während die endgültige Stack-Vorhersage als hierarchische Summe aller Teilvorhersagen modelliert wird. Dieser Prozess simuliert die Box-Jenkins-Methode des ARIMA-Modells.
Interpretierbarkeit: Das Modell gibt es in zwei Varianten, universell und interpretierbar. In der allgemeinen Variante lernt das Netzwerk willkürlich die endgültigen Gewichte der vollständig verbundenen Schichten jedes Blocks. Bei der interpretierbaren Variante wird die letzte Schicht jedes Blocks entfernt. Die Backcast- und Prognosezweige werden dann mit spezifischen Matrizen multipliziert, die den Trend (monotone Funktion) und die Saisonalität (zyklische zyklische Funktion) simulieren.
Hinweis: Die ursprüngliche N-BEATS-Implementierung funktioniert nur mit univariaten Zeitreihen.
DeepAR
Ein neuartiges Zeitreihenmodell, das Deep Learning und autoregressive Funktionen kombiniert. Abbildung 2 zeigt die Top-Level-Architektur von DeepAR:
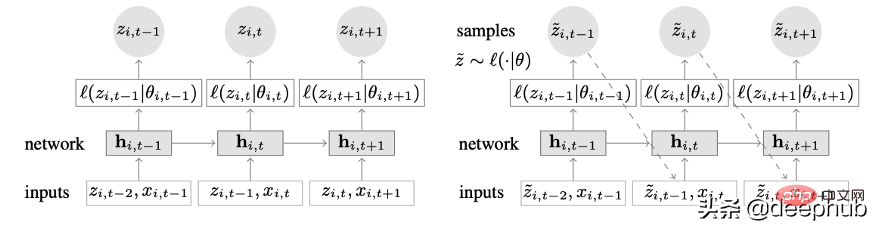
Hier sind die Hauptvorteile dieses Modells:
DeepAR funktioniert sehr gut mit mehreren Zeitreihen: Ein globales Modell wird durch die Verwendung mehrerer Zeitreihen mit leicht unterschiedlichen Verteilungen erstellt. Auch auf viele reale Szenarien anwendbar. Beispielsweise möchte ein Energieversorger möglicherweise einen Energieprognosedienst für jeden Kunden einführen, der unterschiedliche Verbrauchsmuster (und damit unterschiedliche Verteilungen) aufweist.
Neben historischen Daten ermöglicht DeepAR auch die Verwendung bekannter zukünftiger Zeitreihen (ein Merkmal autoregressiver Modelle) und zusätzlicher statischer Attribute. Im zuvor erwähnten Szenario zur Prognose des Strombedarfs könnte eine zusätzliche Zeitvariable der Monat sein (als Ganzzahl mit einem Wert zwischen 1 und 12). Unter der Annahme, dass jedem Kunden ein Sensor zugeordnet ist, der den Stromverbrauch misst, wären die zusätzlichen statischen Variablen etwa sensor_id oder customer_id.
Wenn Sie mit der Verwendung neuronaler Netzwerkarchitekturen wie MLPs und RNNs für die Zeitreihenvorhersage vertraut sind, besteht ein wichtiger Vorverarbeitungsschritt darin, die Zeitreihen mithilfe von Normalisierungs- oder Normalisierungstechniken zu skalieren. Dies erfordert keinen manuellen Vorgang in DeepAR, da das zugrunde liegende Modell die autoregressive Eingabe z für jede Zeitreihe i um einen Skalierungsfaktor v_i skaliert, der dem Mittelwert dieser Zeitreihe entspricht. Konkret lautet die im Benchmark des Papiers verwendete Skalierungsfaktorgleichung wie folgt:

Aber in der Praxis, wenn die Größe der Zielzeitreihe stark variiert, ist es immer noch notwendig, während der Vorverarbeitung eine eigene Skalierung anzuwenden. In einem Energiebedarfsprognoseszenario kann der Datensatz beispielsweise Mittelspannungsstromkunden (z. B. kleine Fabriken, die Strom in Megawatteinheiten verbrauchen) und Niederspannungskunden (z. B. Haushalte, die Strom in Kilowatteinheiten verbrauchen) enthalten.
DeepAR macht probabilistische Vorhersagen, anstatt zukünftige Werte direkt auszugeben. Dies erfolgt als Monte-Carlo-Stichprobe. Diese Vorhersagen werden verwendet, um Quantilvorhersagen mithilfe der Quantilverlustfunktion zu berechnen. Für diejenigen, die mit dieser Art von Verlust nicht vertraut sind: Quantilverlust wird nicht nur zur Berechnung einer Schätzung, sondern eines Vorhersageintervalls um diesen Wert herum verwendet.
Spacetimeformer
Die Zeitabhängigkeit ist in univariaten Zeitreihen am wichtigsten. Aber in Szenarien mit mehreren Zeitreihen sind die Dinge nicht so einfach. Angenommen, wir haben eine Wettervorhersageaufgabe und möchten die Temperatur von fünf Städten vorhersagen. Nehmen wir an, diese Städte gehören zu einem Land. Angesichts dessen, was wir bisher gesehen haben, können wir DeepAR verwenden und jede Stadt als externe statische Kovariate modellieren.
Mit anderen Worten: Das Modell berücksichtigt sowohl zeitliche als auch räumliche Beziehungen. Dies ist die Kernidee von Spacetimeformer: Nutzen Sie ein Modell, um die räumlichen Beziehungen zwischen diesen Städten/Orten auszunutzen und lernen Sie so zusätzliche nützliche Abhängigkeiten kennen, da das Modell sowohl zeitliche als auch räumliche Beziehungen berücksichtigt.
Eingehende Untersuchung von Raum-Zeit-Sequenzen
Wie der Name schon sagt, verwendet dieses Modell intern eine transformatorbasierte Struktur. Bei der Verwendung transformatorbasierter Modelle zur Zeitreihenvorhersage besteht eine beliebte Technik zur Erzeugung zeitbewusster Einbettungen darin, die Eingabe durch eine Time2Vec [6]-Einbettungsschicht zu leiten (für NLP-Aufgaben werden Positionskodierungsvektoren anstelle von Time2Vec verwendet). Während diese Technik für univariate Zeitreihen gut funktioniert, ist sie für multivariate Zeiteingaben nicht sinnvoll. Es kann sein, dass bei der Sprachmodellierung jedes Wort in einem Satz durch eine Einbettung dargestellt wird und ein Wort im Wesentlichen ein Teil des Vokabulars ist, während Zeitreihen nicht so einfach sind.
In multivariaten Zeitreihen hat die Eingabe zu einem bestimmten Zeitschritt t die Form x_1,t, x2,t, x_m,t, wobei x_i,t der Wert von Merkmal i und m die Gesamtzahl der Merkmale ist /Sequenzen. Wenn wir die Eingabe durch eine Time2Vec-Ebene leiten, wird ein zeitlicher Einbettungsvektor erzeugt. Was stellt diese Einbettung wirklich dar? Die Antwort ist, dass sie die gesamte Eingabesammlung als eine einzige Entität (Token) darstellt. Das Modell lernt also nur die zeitliche Dynamik zwischen Zeitschritten, vermisst jedoch die räumlichen Beziehungen zwischen Merkmalen/Variablen.
Spacetimeformer löst dieses Problem, indem es die Eingabe in einen großen Vektor namens Raumzeitsequenz abflacht. Wenn die Eingabe N Variablen enthält, die in T Zeitschritten organisiert sind, erhält die resultierende raumzeitliche Sequenz die Bezeichnung (NxT). Abbildung 3 unten zeigt dies besser:
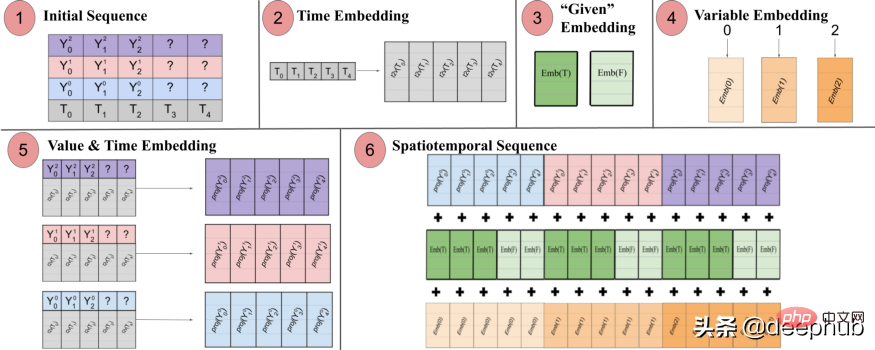
In dem Papier heißt es: „(1) Multivariates Eingabeformat, das Zeitinformationen enthält. Der Decoder-Eingabe fehlen („?“) Werte und wird bei Vorhersagen auf Null gesetzt. (2) Die Zeitreihe wird durch eine Time2Vec-Schicht geleitet um eine Darstellung der Periodizität zu erzeugen. Frequenzeinbettung des Eingabemusters (3) Die binäre Einbettung gibt an, ob der Wert als Kontext angegeben wird oder vorhergesagt werden muss. (4) Zuordnung des ganzzahligen Index jeder Zeitreihe zu einer „räumlichen“ Darstellung mit einer Nachschlagetabelleneinbettung. 5) Die Verwendung einer Feedforward-Ebene zur Projektion der Time2Vec-Einbettung und der Variablenwerte jeder Zeitreihe. (6) Das Summieren von Werten und Zeit, Variablen und gegebenen Einbettungen führt dazu, dass die MSA zwischen Zeit und Variable länger wird Leerzeichen.
Mit anderen Worten, die endgültige Sequenz kodiert eine einheitliche Einbettung, die zeitliche, räumliche und kontextuelle Informationen enthält. Ein Nachteil dieser Methode ist jedoch, dass die Sequenz sehr lang werden kann, was zu einem sekundären Ressourcenwachstum führt. Dies liegt daran, dass gemäß dem Aufmerksamkeitsmechanismus jedes Token mit dem anderen verglichen wird. Der Autor verwendet eine effizientere Architektur namens Performer-Aufmerksamkeitsmechanismus, die für größere Sequenzen geeignet ist Von Google veröffentlichtes Serienvorhersagemodell. TFT ist vielseitiger als frühere Modelle. Die Top-Level-Architektur von TFT ist in Abbildung 4 dargestellt. :
Wie die zuvor genannten Modelle unterstützt TFT die Erstellung von Modellen auf mehreren heterogenen Zeitreihen
TFT unterstützt Drei Arten von Merkmalen: i) Zeitveränderliche Daten mit bekannten zukünftigen Eingaben ii) Bisher bekannte zeitveränderliche Daten iii) Kategorische/statische Variablen, auch als zeitinvariante Merkmale bekannt In dem zuvor erwähnten Szenario zur Vorhersage des Strombedarfs möchten wir die Luftfeuchtigkeit als Funktion verwenden, die bisher nur in TFT möglich war, in DeepAR jedoch nicht. Abbildung 5 zeigt ein Beispiel So nutzen Sie alle diese Funktionen:
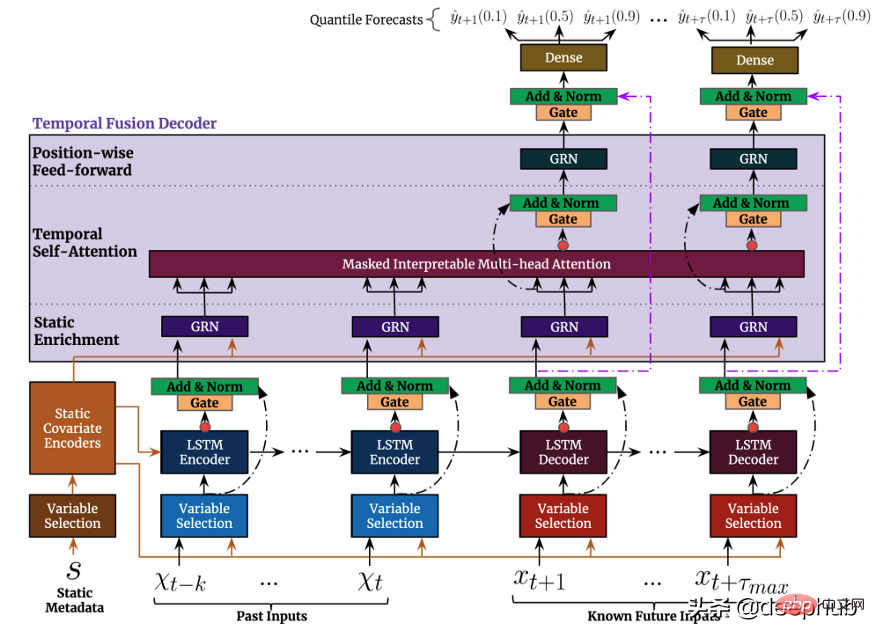
TFT wird besonders durch die Nutzung der Variablenauswahlkomponente (siehe Abbildung 4 oben) hervorgehoben Andererseits kann man sagen, dass das Modell die Wichtigkeit des Merkmals lernt. Es wird ein neuer interpretierbarer Multi-Head-Aufmerksamkeitsmechanismus vorgeschlagen: Die Aufmerksamkeitsgewichte dieser Ebene können zeigen, welche Zeitschritte während des Überprüfungszeitraums am wichtigsten sind kann die bedeutendsten saisonalen Muster im gesamten Datensatz aufdecken: Ähnlich wie DeepAR gibt TFT Vorhersageintervalle und Vorhersagewerte mithilfe der Quantilregression aus.
Zusammenfassend lässt sich sagen, dass Deep Learning darüber hinaus zweifellos die Landschaft der Zeitreihenvorhersage revolutioniert hat zu einer beispiellosen Leistung: Sie nutzen vielfältige, multivariate Zeitdaten vollständig aus und nutzen exogene Informationen, um die Prognoseleistung auf ein beispielloses Niveau zu steigern. Allerdings nutzen die meisten NLP-Aufgaben (Natural Language Processing) vorab trainierte Modelle. Der Feed von NLP-Aufgaben besteht größtenteils aus von Menschen erstellten Daten. Sie sind voller reichhaltiger und hervorragender Informationen und können fast als Dateneinheit betrachtet werden. Bei der Zeitreihenvorhersage können wir den Mangel an solchen vorab trainierten Modellen spüren. Warum können wir uns das nicht in Zeitreihen zunutze machen, wie wir es im NLP tun?
Dies führt zum letzten Modell, das wir vorstellen möchten, TSFormer. Dieses Modell berücksichtigt zwei Perspektiven. Wir unterteilen es in vier Teile von der Eingabe bis zur Ausgabe und stellen Python-Implementierungscode bereit (offiziell auch bereitgestellt). Das Modell wurde gerade veröffentlicht. Deshalb konzentrieren wir uns hier darauf.
TSFormer
Es handelt sich um ein unbeaufsichtigtes Zeitreihen-Pre-Training-Modell auf Basis von Transformer (TSFormer), das die Trainingsstrategie in MAE nutzt und in der Lage ist, sehr lange Abhängigkeiten in den Daten zu erfassen. 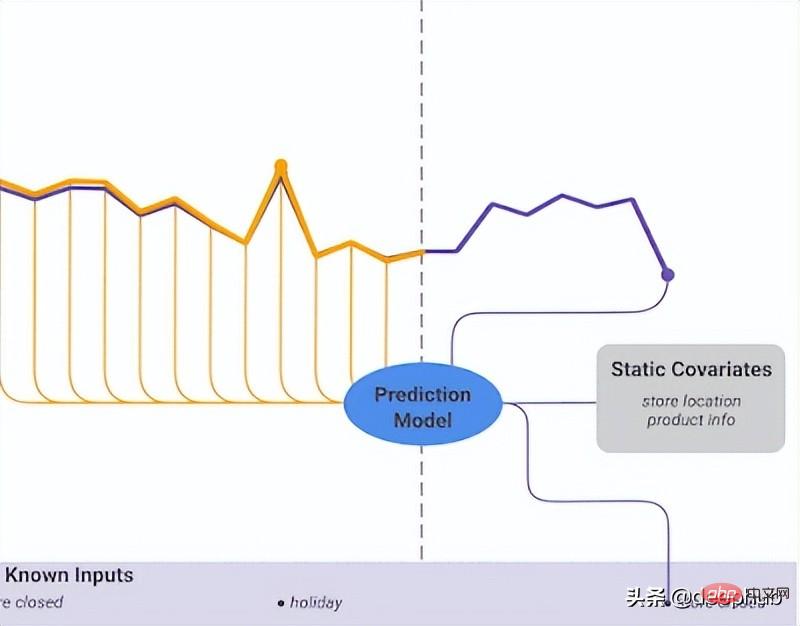
Die Dichte von Zeitreihendaten ist viel geringer als bei Daten in natürlicher Sprache
Wir benötigen längere Zeitreihendaten als NLP-Daten
Einführung in TSFormerTSFormer ähnelt im Wesentlichen der Hauptarchitektur von MAE. Die Daten durchlaufen einen Encoder und dann einen Decoder ) maskierte) Daten.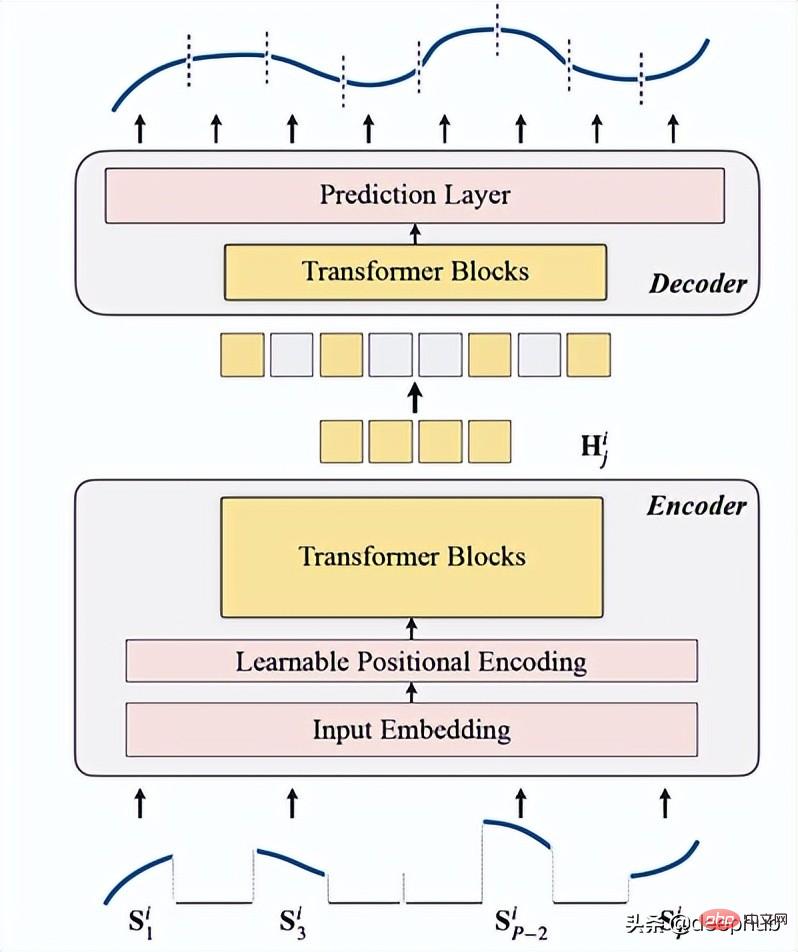
Wir fassen es in den folgenden 4 Punkten zusammen:
1. Die Maskierung
ist der erste Schritt, bevor Daten in den Encoder gelangen. Die Eingabesequenz (Sᶦ) wurde in P Scheiben verteilt, deren Länge L ist. Daher beträgt die Länge des Schiebefensters, das zur Vorhersage des nächsten Zeitschritts verwendet wird, P XL.

Das Maskierungsverhältnis beträgt 75 % (es sieht sehr hoch aus, wahrscheinlich weil es die gleichen Parameter wie MAE verwendet). Was wir erledigen wollen, ist eine selbstüberwachte Aufgabe, also je weniger Daten, desto schneller die Berechnung des Encoders Geschwindigkeit.
Der Hauptgrund dafür (Maskierung von Eingabesequenzsegmenten) ist:
- Segmente (Patch) sind besser als einzelne Punkte.
- Es vereinfacht die Verwendung von Downstream-Modellen (STGNN verwendet Einheitssegmente als Eingabe)
- kann die Eingabegröße des Encoders faktorisieren.
class Patch(nn.Module):<br>def __init__(self, patch_size, input_channel, output_channel, spectral=True):<br>super().__init__()<br>self.output_channel = output_channel<br>self.P = patch_size<br>self.input_channel = input_channel<br>self.output_channel = output_channel<br>self.spectral = spectral<br>if spectral:<br>self.emb_layer = nn.Linear(int(patch_size/2+1)*2, output_channel)<br>else:<br>self.input_embedding = nn.Conv2d(input_channel, output_channel, kernel_size=(self.P, 1), stride=(self.P, 1))<br>def forward(self, input):<br>B, N, C, L = input.shape<br>if self.spectral:<br>spec_feat_ = torch.fft.rfft(input.unfold(-1, self.P, self.P), dim=-1)<br>real = spec_feat_.real<br>imag = spec_feat_.imag<br>spec_feat = torch.cat([real, imag], dim=-1).squeeze(2)<br>output = self.emb_layer(spec_feat).transpose(-1, -2)<br>else:<br>input = input.unsqueeze(-1) # B, N, C, L, 1<br>input = input.reshape(B*N, C, L, 1) # B*N, C, L, 1<br>output = self.input_embedding(input) # B*N, d, L/P, 1<br>output = output.squeeze(-1).view(B, N, self.output_channel, -1)<br>assert output.shape[-1] == L / self.P<br>return output
Die folgende Funktion generiert eine Maskierung:
class MaskGenerator(nn.Module):<br>def __init__(self, mask_size, mask_ratio, distribution='uniform', lm=-1):<br>super().__init__()<br>self.mask_size = mask_size<br>self.mask_ratio = mask_ratio<br>self.sort = True<br>self.average_patch = lm<br>self.distribution = distribution<br>if self.distribution == "geom":<br>assert lm != -1<br>assert distribution in ['geom', 'uniform']<br>def uniform_rand(self):<br>mask = list(range(int(self.mask_size)))<br>random.shuffle(mask)<br>mask_len = int(self.mask_size * self.mask_ratio)<br>self.masked_tokens = mask[:mask_len]<br>self.unmasked_tokens = mask[mask_len:]<br>if self.sort:<br>self.masked_tokens = sorted(self.masked_tokens)<br>self.unmasked_tokens = sorted(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def geometric_rand(self):<br>mask = geom_noise_mask_single(self.mask_size, lm=self.average_patch, masking_ratio=self.mask_ratio) # 1: masked, 0:unmasked<br>self.masked_tokens = np.where(mask)[0].tolist()<br>self.unmasked_tokens = np.where(~mask)[0].tolist()<br># assert len(self.masked_tokens) > len(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def forward(self):<br>if self.distribution == 'geom':<br>self.unmasked_tokens, self.masked_tokens = self.geometric_rand()<br>elif self.distribution == 'uniform':<br>self.unmasked_tokens, self.masked_tokens = self.uniform_rand()<br>else:<br>raise Exception("ERROR")<br>return self.unmasked_tokens, self.masked_tokens2. Kodierung
umfasst Eingabeeinbettung, Positionskodierung und Transformer-Block. Der Encoder kann nur auf unmaskierten Patches ausgeführt werden (dies ist auch die MAE-Methode).
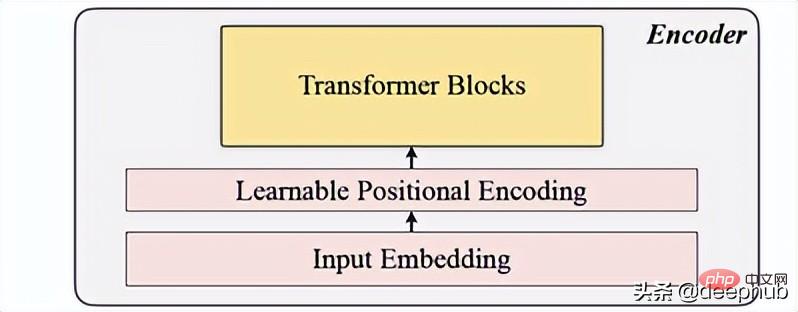
Eingabeeinbettung
Verwendet eine lineare Projektion, um die Eingabeeinbettung zu erhalten, die den nicht maskierten Raum in einen latenten Raum umwandelt. Die Formel ist unten zu sehen:
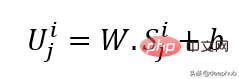
W und B sind die lernbaren Parameter und U ist der Modelleingabevektor in der Dimension.
Positionskodierung
Eine einfache Positionskodierungsschicht wird verwendet, um neue sequentielle Informationen anzuhängen. Das Wort „lernbar“ wurde hinzugefügt, um eine bessere Leistung als Sinus anzuzeigen. Daher zeigen lernbare Standorteinbettungen gute Ergebnisse für Zeitreihen.
class LearnableTemporalPositionalEncoding(nn.Module):<br>def __init__(self, d_model, dropout=0.1, max_len: int = 1000):<br>super().__init__()<br>self.dropout = nn.Dropout(p=dropout)<br>self.pe = nn.Parameter(torch.empty(max_len, d_model), requires_grad=True)<br>nn.init.uniform_(self.pe, -0.02, 0.02)<br><br>def forward(self, X, index):<br>if index is None:<br>pe = self.pe[:X.size(1), :].unsqueeze(0)<br>else:<br>pe = self.pe[index].unsqueeze(0)<br>X = X + pe<br>X = self.dropout(X)<br>return X<br>class PositionalEncoding(nn.Module):<br>def __init__(self, hidden_dim, dropout=0.1):<br>super().__init__()<br>self.tem_pe = LearnableTemporalPositionalEncoding(hidden_dim, dropout)<br>def forward(self, input, index=None, abs_idx=None):<br>B, N, L_P, d = input.shape<br># temporal embedding<br>input = self.tem_pe(input.view(B*N, L_P, d), index=index)<br>input = input.view(B, N, L_P, d)<br># absolute positional embedding<br>return input
Transformer-Block
Das Papier verwendet 4 Schichten von Transformers, was eine geringere Anzahl ist, als es bei Computer Vision und Verarbeitungsaufgaben natürlicher Sprache üblich ist. Der hier verwendete Transformer ist die grundlegendste Struktur, die im Originalpapier erwähnt wird, wie in Abbildung 4 unten dargestellt:
class TransformerLayers(nn.Module):<br>def __init__(self, hidden_dim, nlayers, num_heads=4, dropout=0.1):<br>super().__init__()<br>self.d_model = hidden_dim<br>encoder_layers = TransformerEncoderLayer(hidden_dim, num_heads, hidden_dim*4, dropout)<br>self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)<br>def forward(self, src):<br>B, N, L, D = src.shape<br>src = src * math.sqrt(self.d_model)<br>src = src.view(B*N, L, D)<br>src = src.transpose(0, 1)<br>output = self.transformer_encoder(src, mask=None)<br>output = output.transpose(0, 1).view(B, N, L, D)<br>return output
3. Dekodierung
Der Decoder enthält eine Reihe von Transformer-Blöcken. Es gilt für alle Patches (im Gegensatz dazu verfügt MAE über keine Positionseinbettung, da seine Patches bereits über Positionsinformationen verfügen), und die Anzahl der Ebenen beträgt nur eins. Anschließend wird ein einfaches MLP verwendet, wodurch die Ausgabelänge jedem Patch entspricht. Länge.
4. Rekonstruktionsziel

Berechnen Sie den Maskierungsfleck für jeden Datenpunkt (i) und wählen Sie mae (Mean-Absolute-Error) als Verlustfunktion der Hauptsequenz und der rekonstruierten Sequenz.

Dies ist die Gesamtarchitektur
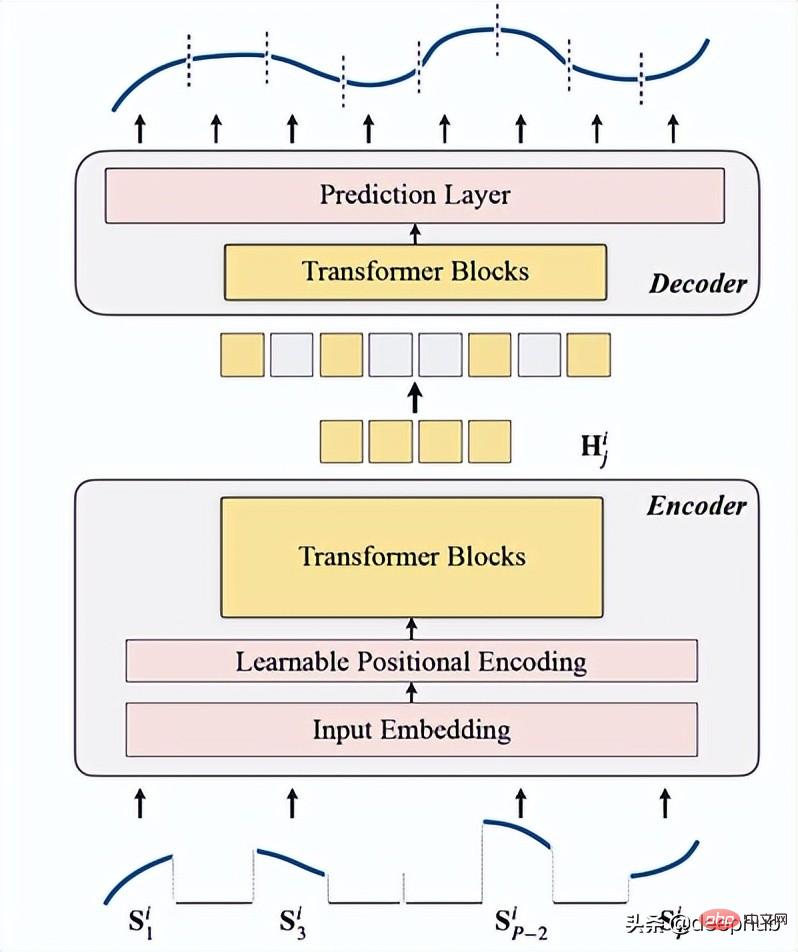
Das Folgende ist die Code-Implementierung:
def trunc_normal_(tensor, mean=0., std=1.):<br>__call_trunc_normal_(tensor, mean=mean, std=std, a=-std, b=std)<br>def unshuffle(shuffled_tokens):<br>dic = {}<br>for k, v, in enumerate(shuffled_tokens):<br>dic[v] = k<br>unshuffle_index = []<br>for i in range(len(shuffled_tokens)):<br>unshuffle_index.append(dic[i])<br>return unshuffle_index<br>class TSFormer(nn.Module):<br>def __init__(self, patch_size, in_channel, out_channel, dropout, mask_size, mask_ratio, L=6, distribution='uniform', lm=-1, selected_feature=0, mode='Pretrain', spectral=True):<br>super().__init__()<br>self.patch_size = patch_size<br>self.seleted_feature = selected_feature<br>self.mode = mode<br>self.spectral = spectral<br>self.patch = Patch(patch_size, in_channel, out_channel, spectral=spectral)<br>self.pe = PositionalEncoding(out_channel, dropout=dropout)<br>self.mask = MaskGenerator(mask_size, mask_ratio, distribution=distribution, lm=lm)<br>self.encoder = TransformerLayers(out_channel, L)<br>self.decoder = TransformerLayers(out_channel, 1)<br>self.encoder_2_decoder = nn.Linear(out_channel, out_channel)<br>self.mask_token = nn.Parameter(torch.zeros(1, 1, 1, out_channel))<br>trunc_normal_(self.mask_token, std=.02)<br>if self.spectral:<br>self.output_layer = nn.Linear(out_channel, int(patch_size/2+1)*2)<br>else:<br>self.output_layer = nn.Linear(out_channel, patch_size)<br>def _forward_pretrain(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br><br># mask tokens<br>unmasked_token_index, masked_token_index = self.mask()<br>encoder_input = patches[:, :, unmasked_token_index, :] <br># encoder<br>H = self.encoder(encoder_input) <br># encoder to decoder<br>H = self.encoder_2_decoder(H)<br># decoder<br># H_unmasked = self.pe(H, index=unmasked_token_index)<br>H_unmasked = H<br>H_masked = self.pe(self.mask_token.expand(B, N, len(masked_token_index), H.shape[-1]), index=masked_token_index)<br>H_full = torch.cat([H_unmasked, H_masked], dim=-2) # # B, N, L/P, d<br>H = self.decoder(H_full)<br># output layer<br>if self.spectral:<br># output = H<br>spec_feat_H_ = self.output_layer(H)<br>real = spec_feat_H_[..., :int(self.patch_size/2+1)]<br>imag = spec_feat_H_[..., int(self.patch_size/2+1):]<br>spec_feat_H = torch.complex(real, imag)<br>out_full = torch.fft.irfft(spec_feat_H)<br>else:<br>out_full = self.output_layer(H)<br># prepare loss<br>B, N, _, _ = out_full.shape <br>out_masked_tokens = out_full[:, :, len(unmasked_token_index):, :]<br>out_masked_tokens = out_masked_tokens.view(B, N, -1).transpose(1, 2)<br>label_full = input.permute(0, 3, 1, 2).unfold(1, self.patch_size, self.patch_size)[:, :, :, self.seleted_feature, :].transpose(1, 2) # B, N, L/P, P<br>label_masked_tokens = label_full[:, :, masked_token_index, :].contiguous()<br>label_masked_tokens = label_masked_tokens.view(B, N, -1).transpose(1, 2)<br># prepare plot<br>## note that the output_full and label_full are not aligned. The out_full in shuffled<br>### therefore, unshuffle for plot<br>unshuffled_index = unshuffle(unmasked_token_index + masked_token_index)<br>out_full_unshuffled = out_full[:, :, unshuffled_index, :]<br>plot_args = {}<br>plot_args['out_full_unshuffled'] = out_full_unshuffled<br>plot_args['label_full'] = label_full<br>plot_args['unmasked_token_index'] = unmasked_token_index<br>plot_args['masked_token_index'] = masked_token_index<br>return out_masked_tokens, label_masked_tokens, plot_args<br>def _forward_backend(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br>encoder_input = patches # no mask when running the backend.<br># encoder<br>H = self.encoder(encoder_input) <br>return H<br>def forward(self, input_data):<br><br>if self.mode == 'Pretrain':<br>return self._forward_pretrain(input_data)<br>else:<br>return self._forward_backend(input_data)Nachdem ich dieses Papier gelesen hatte, stellte ich fest, dass es sich im Grunde genommen um eine Kopie von MAE oder MAE von Zeitreihen handelt Die Vorhersagephase ähnelt auch der von MAE. Sie verwendet die Ausgabe des Encoders als Eingabe für nachgelagerte Aufgaben. Wenn Sie interessiert sind, können Sie sich den darin bereitgestellten Code ansehen Papier.
Das obige ist der detaillierte Inhalt vonVergleichszusammenfassung von fünf Deep-Learning-Modellen für die Zeitreihenvorhersage. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1370
1370
 52
52
 Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Heute diskutieren wir darüber, wie Deep-Learning-Technologie die Leistung von visionbasiertem SLAM (Simultaneous Localization and Mapping) in komplexen Umgebungen verbessern kann. Durch die Kombination von Methoden zur Tiefenmerkmalsextraktion und Tiefenanpassung stellen wir hier ein vielseitiges hybrides visuelles SLAM-System vor, das die Anpassung in anspruchsvollen Szenarien wie schlechten Lichtverhältnissen, dynamischer Beleuchtung, schwach strukturierten Bereichen und starkem Jitter verbessern soll. Unser System unterstützt mehrere Modi, einschließlich erweiterter Monokular-, Stereo-, Monokular-Trägheits- und Stereo-Trägheitskonfigurationen. Darüber hinaus wird analysiert, wie visuelles SLAM mit Deep-Learning-Methoden kombiniert werden kann, um andere Forschungen zu inspirieren. Durch umfangreiche Experimente mit öffentlichen Datensätzen und selbst abgetasteten Daten demonstrieren wir die Überlegenheit von SL-SLAM in Bezug auf Positionierungsgenauigkeit und Tracking-Robustheit.
 Quantilregression für probabilistische Zeitreihenprognosen
May 07, 2024 pm 05:04 PM
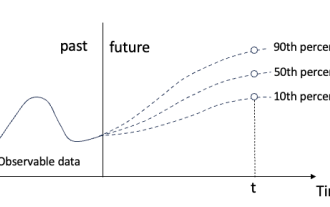
Quantilregression für probabilistische Zeitreihenprognosen
May 07, 2024 pm 05:04 PM
Ändern Sie nicht die Bedeutung des ursprünglichen Inhalts, optimieren Sie den Inhalt nicht, schreiben Sie den Inhalt neu und fahren Sie nicht fort. „Die Quantilregression erfüllt diesen Bedarf, indem sie Vorhersageintervalle mit quantifizierten Chancen bereitstellt. Dabei handelt es sich um eine statistische Technik zur Modellierung der Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen, insbesondere wenn die bedingte Verteilung der Antwortvariablen von Interesse ist. Im Gegensatz zur herkömmlichen Regression Methoden: Die Quantilregression konzentriert sich auf die Schätzung der bedingten Größe der Antwortvariablen und nicht auf den bedingten Mittelwert Quantile der erklärten Variablen Y. Das bestehende Regressionsmodell ist eigentlich eine Methode zur Untersuchung der Beziehung zwischen der erklärten Variablen und der erklärenden Variablen. Sie konzentrieren sich auf die Beziehung zwischen erklärenden Variablen und erklärten Variablen
 „Defect Spectrum' durchbricht die Grenzen der herkömmlichen Fehlererkennung und erreicht erstmals eine hochpräzise und umfassende semantische Fehlererkennung in der Industrie.
Jul 26, 2024 pm 05:38 PM
„Defect Spectrum' durchbricht die Grenzen der herkömmlichen Fehlererkennung und erreicht erstmals eine hochpräzise und umfassende semantische Fehlererkennung in der Industrie.
Jul 26, 2024 pm 05:38 PM
In der modernen Fertigung ist die genaue Fehlererkennung nicht nur der Schlüssel zur Sicherstellung der Produktqualität, sondern auch der Kern für die Verbesserung der Produktionseffizienz. Allerdings mangelt es vorhandenen Datensätzen zur Fehlererkennung häufig an der Genauigkeit und dem semantischen Reichtum, die für praktische Anwendungen erforderlich sind, was dazu führt, dass Modelle bestimmte Fehlerkategorien oder -orte nicht identifizieren können. Um dieses Problem zu lösen, hat ein Spitzenforschungsteam bestehend aus der Hong Kong University of Science and Technology Guangzhou und Simou Technology innovativ den „DefectSpectrum“-Datensatz entwickelt, der eine detaillierte und semantisch reichhaltige groß angelegte Annotation von Industriedefekten ermöglicht. Wie in Tabelle 1 gezeigt, bietet der Datensatz „DefectSpectrum“ im Vergleich zu anderen Industriedatensätzen die meisten Fehleranmerkungen (5438 Fehlerproben) und die detaillierteste Fehlerklassifizierung (125 Fehlerkategorien).
 Das NVIDIA-Dialogmodell ChatQA wurde auf Version 2.0 weiterentwickelt, wobei die angegebene Kontextlänge 128 KB beträgt
Jul 26, 2024 am 08:40 AM
Das NVIDIA-Dialogmodell ChatQA wurde auf Version 2.0 weiterentwickelt, wobei die angegebene Kontextlänge 128 KB beträgt
Jul 26, 2024 am 08:40 AM
Die offene LLM-Community ist eine Ära, in der hundert Blumen blühen und konkurrieren. Sie können Llama-3-70B-Instruct, QWen2-72B-Instruct, Nemotron-4-340B-Instruct, Mixtral-8x22BInstruct-v0.1 und viele andere sehen hervorragende Darsteller. Allerdings weisen offene Modelle im Vergleich zu den proprietären Großmodellen GPT-4-Turbo in vielen Bereichen noch erhebliche Lücken auf. Zusätzlich zu allgemeinen Modellen wurden einige offene Modelle entwickelt, die sich auf Schlüsselbereiche spezialisieren, wie etwa DeepSeek-Coder-V2 für Programmierung und Mathematik und InternVL für visuelle Sprachaufgaben.
 Google AI gewann die Silbermedaille der IMO Mathematical Olympiad, das mathematische Argumentationsmodell AlphaProof wurde eingeführt und Reinforcement Learning ist zurück
Jul 26, 2024 pm 02:40 PM
Google AI gewann die Silbermedaille der IMO Mathematical Olympiad, das mathematische Argumentationsmodell AlphaProof wurde eingeführt und Reinforcement Learning ist zurück
Jul 26, 2024 pm 02:40 PM
Für KI ist die Mathematikolympiade kein Problem mehr. Am Donnerstag hat die künstliche Intelligenz von Google DeepMind eine Meisterleistung vollbracht: Sie nutzte KI, um meiner Meinung nach die eigentliche Frage der diesjährigen Internationalen Mathematikolympiade zu lösen, und war nur einen Schritt davon entfernt, die Goldmedaille zu gewinnen. Der IMO-Wettbewerb, der gerade letzte Woche zu Ende ging, hatte sechs Fragen zu Algebra, Kombinatorik, Geometrie und Zahlentheorie. Das von Google vorgeschlagene hybride KI-System beantwortete vier Fragen richtig und erzielte 28 Punkte und erreichte damit die Silbermedaillenstufe. Anfang dieses Monats hatte der UCLA-Professor Terence Tao gerade die KI-Mathematische Olympiade (AIMO Progress Award) mit einem Millionenpreis gefördert. Unerwarteterweise hatte sich das Niveau der KI-Problemlösung vor Juli auf dieses Niveau verbessert. Beantworten Sie die Fragen meiner Meinung nach gleichzeitig. Am schwierigsten ist es meiner Meinung nach, da sie die längste Geschichte, den größten Umfang und die negativsten Fragen haben
 Training mit Millionen von Kristalldaten zur Lösung kristallographischer Phasenprobleme, die Deep-Learning-Methode PhAI wird in Science veröffentlicht
Aug 08, 2024 pm 09:22 PM
Training mit Millionen von Kristalldaten zur Lösung kristallographischer Phasenprobleme, die Deep-Learning-Methode PhAI wird in Science veröffentlicht
Aug 08, 2024 pm 09:22 PM
Herausgeber |KX Bis heute sind die durch die Kristallographie ermittelten Strukturdetails und Präzision, von einfachen Metallen bis hin zu großen Membranproteinen, mit keiner anderen Methode zu erreichen. Die größte Herausforderung, das sogenannte Phasenproblem, bleibt jedoch die Gewinnung von Phaseninformationen aus experimentell bestimmten Amplituden. Forscher der Universität Kopenhagen in Dänemark haben eine Deep-Learning-Methode namens PhAI entwickelt, um Kristallphasenprobleme zu lösen. Ein Deep-Learning-Neuronales Netzwerk, das mithilfe von Millionen künstlicher Kristallstrukturen und den entsprechenden synthetischen Beugungsdaten trainiert wird, kann genaue Elektronendichtekarten erstellen. Die Studie zeigt, dass diese Deep-Learning-basierte Ab-initio-Strukturlösungsmethode das Phasenproblem mit einer Auflösung von nur 2 Angström lösen kann, was nur 10 bis 20 % der bei atomarer Auflösung verfügbaren Daten im Vergleich zur herkömmlichen Ab-initio-Berechnung entspricht
 Der Standpunkt der Natur: Die Erprobung künstlicher Intelligenz in der Medizin ist im Chaos. Was ist zu tun?
Aug 22, 2024 pm 04:37 PM
Der Standpunkt der Natur: Die Erprobung künstlicher Intelligenz in der Medizin ist im Chaos. Was ist zu tun?
Aug 22, 2024 pm 04:37 PM
Herausgeber | ScienceAI Basierend auf begrenzten klinischen Daten wurden Hunderte medizinischer Algorithmen genehmigt. Wissenschaftler diskutieren darüber, wer die Werkzeuge testen soll und wie dies am besten geschieht. Devin Singh wurde Zeuge, wie ein pädiatrischer Patient in der Notaufnahme einen Herzstillstand erlitt, während er lange auf eine Behandlung wartete, was ihn dazu veranlasste, den Einsatz von KI zu erforschen, um Wartezeiten zu verkürzen. Mithilfe von Triage-Daten aus den Notaufnahmen von SickKids erstellten Singh und Kollegen eine Reihe von KI-Modellen, um mögliche Diagnosen zu stellen und Tests zu empfehlen. Eine Studie zeigte, dass diese Modelle die Zahl der Arztbesuche um 22,3 % verkürzen können und die Verarbeitung der Ergebnisse pro Patient, der einen medizinischen Test benötigt, um fast drei Stunden beschleunigt. Der Erfolg von Algorithmen der künstlichen Intelligenz in der Forschung bestätigt dies jedoch nur
 Um ein neues wissenschaftliches und komplexes Frage-Antwort-Benchmark- und Bewertungssystem für große Modelle bereitzustellen, haben UNSW, Argonne, die University of Chicago und andere Institutionen gemeinsam das SciQAG-Framework eingeführt
Jul 25, 2024 am 06:42 AM
Um ein neues wissenschaftliches und komplexes Frage-Antwort-Benchmark- und Bewertungssystem für große Modelle bereitzustellen, haben UNSW, Argonne, die University of Chicago und andere Institutionen gemeinsam das SciQAG-Framework eingeführt
Jul 25, 2024 am 06:42 AM
Herausgeber | Der Frage-Antwort-Datensatz (QA) von ScienceAI spielt eine entscheidende Rolle bei der Förderung der Forschung zur Verarbeitung natürlicher Sprache (NLP). Hochwertige QS-Datensätze können nicht nur zur Feinabstimmung von Modellen verwendet werden, sondern auch effektiv die Fähigkeiten großer Sprachmodelle (LLMs) bewerten, insbesondere die Fähigkeit, wissenschaftliche Erkenntnisse zu verstehen und zu begründen. Obwohl es derzeit viele wissenschaftliche QS-Datensätze aus den Bereichen Medizin, Chemie, Biologie und anderen Bereichen gibt, weisen diese Datensätze immer noch einige Mängel auf. Erstens ist das Datenformular relativ einfach, die meisten davon sind Multiple-Choice-Fragen. Sie sind leicht auszuwerten, schränken jedoch den Antwortauswahlbereich des Modells ein und können die Fähigkeit des Modells zur Beantwortung wissenschaftlicher Fragen nicht vollständig testen. Im Gegensatz dazu offene Fragen und Antworten



