Beispielanalyse einer Hash-Tabelle in Java

1, Konzept

In der sequentiellen Struktur und im ausgeglichenen Baum gibt es keine entsprechende Beziehung zwischen dem Schlüsselcode des Elements und seinem Speicherort. Daher müssen bei der Suche nach einem Element mehrere Vergleiche des Schlüsselcodes durchgeführt werden gemacht. Die zeitliche Komplexität der sequentiellen Suche beträgt O(N). In einem ausgeglichenen Baum ist sie die Höhe des Baumes, d. h. O( ). Die Effizienz der Suche hängt von der Anzahl der Elementvergleiche während des Suchvorgangs ab.

Ideale Suchmethode: Sie können das zu suchende Element ohne Vergleich direkt aus der Tabelle abrufen. Wenn Sie eine Speicherstruktur erstellen und eine bestimmte Funktion (hashFunc) verwenden, um eine Eins-zu-eins-Zuordnungsbeziehung zwischen dem Speicherort des Elements und seinem Schlüsselcode herzustellen, können Sie das Element während der Suche über diese Funktion schnell finden.

Beim Einfügen eines Elements in diese Struktur:

Ein Element einfügen

Verwenden Sie diese Funktion entsprechend dem Schlüsselcode des einzufügenden Elements, um den Speicherort des Elements zu berechnen und es entsprechend diesem Ort zu speichern

Suchen für Elemente

Führen Sie den Schlüsselcode des Elements aus. In derselben Berechnung wird der erhaltene Funktionswert als Speicherort des Elements betrachtet und das Element entsprechend dieser Position in der Struktur verglichen. Wenn die Schlüsselcodes gleich sind, Die Suche ist erfolgreich

Zum Beispiel: Datensatz {1, 7, 6, 4, 5, 9};

Die Hash-Funktion ist eingestellt auf: Hash(Schlüssel) = Schlüssel % Kapazität ist die Gesamtgröße der darunterliegender Raum zum Speichern von Elementen.

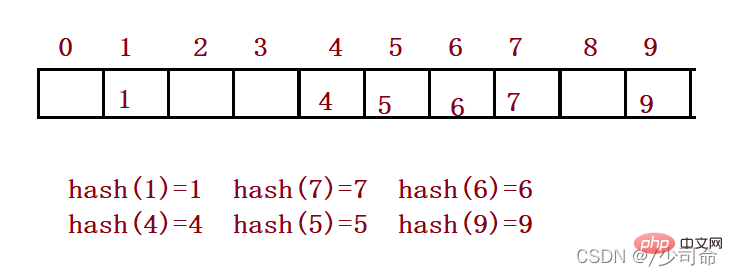
2. Konfliktvermeidung

Zunächst müssen wir klarstellen, dass dies dazu führt, dass die Kapazität des zugrunde liegenden Arrays unserer Hash-Tabelle häufig kleiner ist als die tatsächliche Anzahl der zu speichernden Schlüsselwörter Es ist ein Konfliktproblem, aber was wir tun können, ist, die Konfliktrate so weit wie möglich zu reduzieren.

3, Konfliktvermeidungs-Hash-Funktionsdesign

Gemeinsame Hash-Funktionen

Direkte Anpassungsmethode – (häufig verwendet)

Nehmen Sie eine lineare Funktion des Schlüsselworts als Hash-Adresse: Hash (Schlüssel) = A* Schlüssel + B Vorteile: Einfach und einheitlich Nachteile: Die Verteilung der Schlüsselwörter muss im Voraus bekannt sein. Verwendungsszenarien: Geeignet zum Auffinden relativ kleiner und kontinuierlicher Situationen.

Methode zum Teilen und Belassen des Rests – (häufig verwendet)

Legen Sie die Anzahl der zulässigen Adressen fest Hash-Tabelle Nehmen Sie für m eine Primzahl p, die nicht größer als m ist, aber m am nächsten kommt oder diesem entspricht, als Teiler gemäß der Hash-Funktion: Hash(key) = key% p(p

Quadrieren der mittleren Methode – (Verstehen)

Angenommen, das Schlüsselwort ist 1234 und das Quadrat davon ist 1522756, und die drei Ziffern 227 in der Mitte werden als Hash-Adresse extrahiert Das Beispiel ist das Schlüsselwort 4321, das Quadrat davon ist 18671041 und die mittlere Methode mit drei Ziffern 671 (oder 710) eignet sich besser als die Methode zum Quadrat der Hash-Adresse: Die Verteilung der Schlüsselwörter ist nicht bekannt, die Anzahl der Ziffern jedoch nicht sehr groß Die Konfliktrate wird durch die Reduzierung des Auslastungsfaktors verschleiert. Es ist bekannt, dass die Anzahl der Schlüsselwörter in der Hash-Tabelle unveränderlich ist. Dann können wir nur die Größe des Arrays in der Hash-Tabelle anpassen.

5, Konfliktlösung-geschlossenes Hashing

Geschlossenes Hashing: Wenn ein Hash-Konflikt auftritt und die Hash-Tabelle nicht voll ist, bedeutet dies, dass leere Positionen in der Hash-Tabelle vorhanden sein müssen Der Schlüssel kann an der „nächsten“ leeren Position in der Konfliktposition gespeichert werden.

①Lineare Erkennung

Im obigen Szenario müssen Sie jetzt beispielsweise Element 44 einfügen. Berechnen Sie zunächst die Hash-Adresse über die Hash-Funktion. Der Index ist 4, daher sollte theoretisch 44 an dieser Position eingefügt werden Der Wert wurde bereits an dieser Position platziert. Wenn das Element 4 ist, tritt ein Hash-Konflikt auf. Lineare Erkennung: Beginnen Sie mit der Position, an der der Konflikt auftritt, und führen Sie die Erkennung rückwärts durch, bis die nächste leere Position gefunden wird.

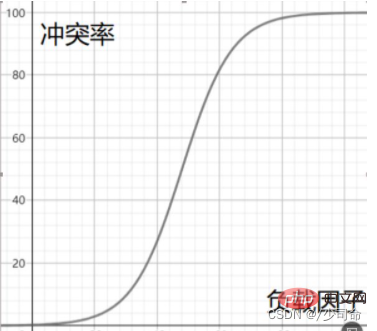Einfügen

Ermitteln Sie die Position des Elements, das in die Hash-Tabelle eingefügt werden soll. Wenn an der Position kein Element vorhanden ist, fügen Sie das neue Element direkt ein Wenn ein Fehler auftritt, verwenden Sie die lineare Erkennung, um das nächste leere Element zu finden.

Wenn Sie geschlossenes Hashing zur Behandlung von Hash-Konflikten verwenden, können Sie vorhandene Elemente in der Hash-Tabelle nicht physisch löschen für andere Elemente. Wenn Sie beispielsweise Element 4 direkt löschen, kann die Suche nach 44 beeinträchtigt sein. Daher verwendet die lineare Prüfung die markierte Pseudolöschung, um ein Element zu löschen.

②Sekundäre Erkennung

Der Fehler der linearen Erkennung besteht darin, dass widersprüchliche Daten gestapelt werden, was mit der Suche nach der nächsten leeren Position zusammenhängt, da der Weg, leere Positionen zu finden, darin besteht, sie einzeln zu finden, sodass die sekundäre Erkennung vermieden werden soll Bei diesem Problem lautet die Methode zum Finden der nächsten leeren Position: = ( + )% m oder: = ( - )% m. Darunter: i = 1,2,3... ist die von der Hash-Funktion Hash(x) berechnete Position auf dem Schlüsselcode des Elements und m ist die Größe der Tabelle. Wenn Sie für 2.1 44 einfügen möchten, tritt nach Verwendung der Lösung ein Konflikt auf:

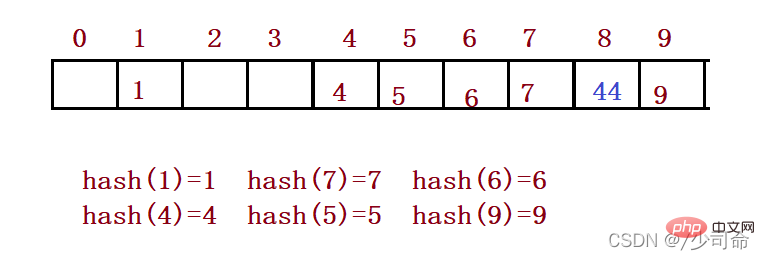
Untersuchungen zeigen, dass die Länge der Tabelle eine Primzahl ist und der Tabellenladefaktor a 0,5 nicht überschreitet , kann das neue Tabellenelement auf jeden Fall eingefügt werden und keine Position wird zweimal untersucht. Daher wird es kein Problem geben, dass die Tabelle voll ist, solange es halb leere Positionen in der Tabelle gibt. Bei der Suche müssen Sie nicht davon ausgehen, dass die Tabelle voll ist. Beim Einfügen müssen Sie jedoch darauf achten, dass der Auslastungsfaktor a der Tabelle 0,5 nicht überschreitet. Bei Überschreitung müssen Sie eine Erhöhung der Kapazität in Betracht ziehen.

6. Conflict-Resolution-Open Hash/Hash Bucket

Die Open-Hash-Methode wird auch als Chain-Adress-Methode (Open-Chain-Methode) bezeichnet. Zunächst wird die Hash-Funktion verwendet, um die Hash-Adresse des Schlüsselcodesatzes zu berechnen. Diejenigen mit denselben Adressschlüsselcodes gehören zur gleichen Teilmenge, und jede Teilmenge wird als Bucket bezeichnet. Die Elemente in jedem Bucket sind durch eine einfach verknüpfte Liste verknüpft, und der Kopfknoten jeder verknüpften Liste wird in gespeichert Hash-Tabelle.

... reee

Das obige ist der detaillierte Inhalt vonBeispielanalyse einer Hash-Tabelle in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!