 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 Wie implementiert man mit Python den PSO-Algorithmus zur Lösung des TSP-Problems?
Wie implementiert man mit Python den PSO-Algorithmus zur Lösung des TSP-Problems?
Wie implementiert man mit Python den PSO-Algorithmus zur Lösung des TSP-Problems?
PSO-Algorithmus
Bevor wir also beginnen, sprechen wir über den grundlegenden PSO-Algorithmus. Der Kern ist nur einer:

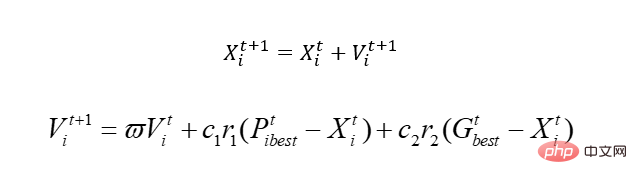
Lassen Sie uns diese Formel erklären, und Sie werden es verstehen.
Alte Regeln: Wir gehen davon aus, dass es eine Gleichung y=sin(x1)+cos(x2) gibt.
Der PSO-Algorithmus realisiert unsere Optimierung durch die Simulation des Vogelzugs. Ich werde nicht näher darauf eingehen, wie es dazu kam, aber lassen Sie uns darüber sprechen Kern .
In der Gleichung, die wir gerade angegeben haben, gibt es zwei Variablen, x1 und x2. Da es sich um einen simulierten Vogel handelt, wird zur Realisierung der Blindmethode hier das Konzept der Geschwindigkeit eingeführt, und x ist natürlich unser realisierbarer Bereich, der der Lösungsraum ist. Durch Änderung der Geschwindigkeit wird x bewegt, das heißt, der Wert von x wird verändert. Unter diesen stellt Pbest die optimale Lösung an dem Ort dar, an dem der Vogel gelaufen ist, und Gbest stellt die optimale Lösung für die gesamte Population dar. Was meinen Sie damit, dass sich dieser Vogel, wenn er sich bewegt, möglicherweise in eine schlechtere Position bewegt, denn im Gegensatz zur Genetik wird er getötet, wenn er schlecht ist, dieser Vogel jedoch nicht. Natürlich gibt es viele lokale Probleme, auf die wir hier nicht eingehen. Kein Algorithmus ist perfekt, und dieser ist richtig.
Algorithmusprozess
Der Hauptprozess des Algorithmus:
Schritt eins: Initialisieren Sie die zufällige Position und Geschwindigkeit des Partikelschwarms und legen Sie die Anzahl der Iterationen fest.
Schritt 2: Berechnen Sie den Fitnesswert jedes Partikels.
Schritt 3: Vergleichen Sie für jedes Partikel seinen Fitnesswert mit dem Fitnesswert der besten Position, die ich erlebt habe. Wenn es besser ist, verwenden Sie es als aktuelle individuelle optimale Position.
Schritt 4: Vergleichen Sie für jedes Partikel seinen Fitnesswert mit dem Fitnesswert der global besten Position, die gbestg erlebt hat. Wenn er besser ist, verwenden Sie ihn als aktuelle globale optimale Position.
Schritt 5: Optimieren Sie die Geschwindigkeit und Position der Partikel gemäß den Geschwindigkeits- und Positionsformeln, um die Partikelposition zu aktualisieren.
Schritt 6: Wenn die Endbedingung nicht erreicht ist (normalerweise die maximale Anzahl von Zyklen oder die minimale Fehleranforderung), kehren Sie zum zweiten Schritt zurück
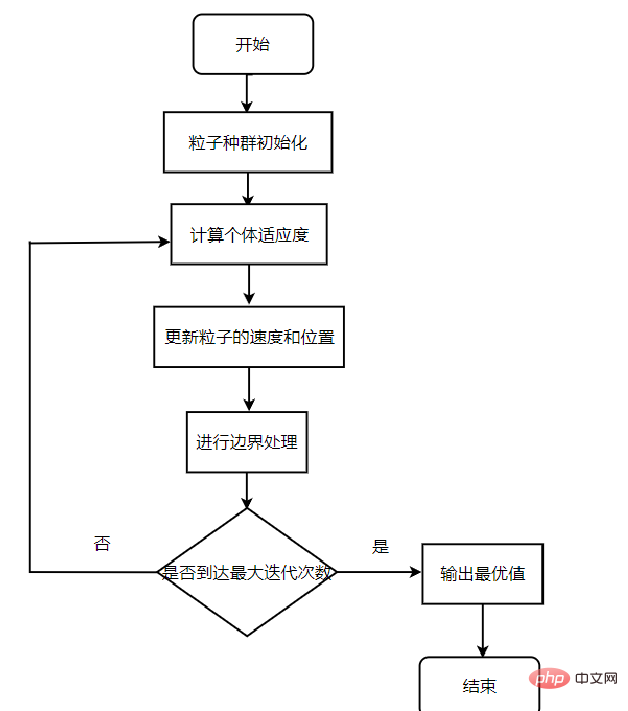
Vorteile:
Der PSO-Algorithmus verfügt nicht über Crossover- und Mutationsoperationen. und verlässt sich auf die Partikelgeschwindigkeit, um die Suche abzuschließen. In der iterativen Entwicklung geben nur die optimalen Partikel Informationen an andere Partikel weiter, und die Suchgeschwindigkeit ist hoch.
Der PSO-Algorithmus verfügt über ein Gedächtnis und die historisch beste Position der Partikelgruppe kann gespeichert und an andere Partikel weitergegeben werden.
Es müssen weniger Parameter angepasst werden, der Aufbau ist einfach und die Implementierung im Engineering ist einfach.
Mithilfe der reellen Zahlenkodierung wird die Anzahl der Variablen in der Problemlösung direkt durch die Lösung des Problems bestimmt und als Dimension des Partikels verwendet.
Nachteile:
fehlt die dynamische Anpassung der Geschwindigkeit und fällt leicht in die lokale Optimalität, was zu einer geringen Konvergenzgenauigkeit und Schwierigkeiten bei der Konvergenz führt.
Diskrete und kombinatorische Optimierungsprobleme können nicht effektiv gelöst werden.
Parameterkontrolle, für verschiedene Probleme, wie man geeignete Parameter auswählt, um optimale Ergebnisse zu erzielen.
kann einige nicht-kartesische Koordinatensystembeschreibungsprobleme nicht effektiv lösen,
einfache Implementierung
ok, werfen wir einen Blick auf die einfachste Implementierung:
import numpy as np
import random
class PSO_model:
def __init__(self,w,c1,c2,r1,r2,N,D,M):
self.w = w # 惯性权值
self.c1=c1
self.c2=c2
self.r1=r1
self.r2=r2
self.N=N # 初始化种群数量个数
self.D=D # 搜索空间维度
self.M=M # 迭代的最大次数
self.x=np.zeros((self.N,self.D)) #粒子的初始位置
self.v=np.zeros((self.N,self.D)) #粒子的初始速度
self.pbest=np.zeros((self.N,self.D)) #个体最优值初始化
self.gbest=np.zeros((1,self.D)) #种群最优值
self.p_fit=np.zeros(self.N)
self.fit=1e8 #初始化全局最优适应度
# 目标函数,也是适应度函数(求最小化问题)
def function(self,x):
A = 10
x1=x[0]
x2=x[1]
Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
return Z
# 初始化种群
def init_pop(self):
for i in range(self.N):
for j in range(self.D):
self.x[i][j] = random.random()
self.v[i][j] = random.random()
self.pbest[i] = self.x[i] # 初始化个体的最优值
aim=self.function(self.x[i]) # 计算个体的适应度值
self.p_fit[i]=aim # 初始化个体的最优位置
if aim < self.fit: # 对个体适应度进行比较,计算出最优的种群适应度
self.fit = aim
self.gbest = self.x[i]
# 更新粒子的位置与速度
def update(self):
for t in range(self.M): # 在迭代次数M内进行循环
for i in range(self.N): # 对所有种群进行一次循环
aim=self.function(self.x[i]) # 计算一次目标函数的适应度
if aim<self.p_fit[i]: # 比较适应度大小,将小的负值给个体最优
self.p_fit[i]=aim
self.pbest[i]=self.x[i]
if self.p_fit[i]<self.fit: # 如果是个体最优再将和全体最优进行对比
self.gbest=self.x[i]
self.fit = self.p_fit[i]
for i in range(self.N): # 更新粒子的速度和位置
self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
self.x[i]=self.x[i]+self.v[i]
print("最优值:",self.fit,"位置为:",self.gbest)
if __name__ == '__main__':
# w,c1,c2,r1,r2,N,D,M参数初始化
w=random.random()
c1=c2=2#一般设置为2
r1=0.7
r2=0.5
N=30
D=2
M=200
pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#设置初始权值
pso_object.init_pop()
pso_object.update()TSP lösen
Datendarstellung
Zuallererst, wenn Sie PSO verwenden , es ist eigentlich dasselbe wie unser bisheriger Einsatz der Genetik. Wir stellen die Bevölkerung immer noch durch eine Matrix dar, und eine Matrix stellt die Entfernung zwischen Städten dar. Was ist der größte Unterschied zwischen
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离,我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()und unserem ursprünglichen PSO? Er ist eigentlich einfach und hängt mit unserer Aktualisierungsgeschwindigkeit zusammen. Wenn wir es mit kontinuierlichen Problemen zu tun haben, ist das tatsächlich so:
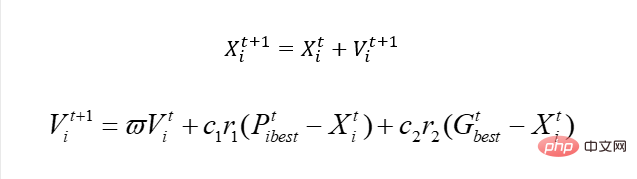
Ebenso können wir X verwenden, um die Nummer der Stadt darzustellen, aber offensichtlich können wir diese Lösung nicht zum Aktualisieren der Geschwindigkeit verwenden.
Wenn wir zu diesem Zeitpunkt die Geschwindigkeit aktualisieren möchten, müssen wir eine neue Lösung verwenden. Diese Lösung ist also tatsächlich das X-Update mit dem genetischen Algorithmus. Um es ganz klar auszudrücken: Der Grund, warum wir Geschwindigkeit brauchen, besteht darin, X zu aktualisieren und X dazu zu bringen, sich in eine gute Richtung zu bewegen. Jetzt ist es nicht mehr möglich, einfach die Geschwindigkeitsaktualisierung zu verwenden, also aktualisieren wir X trotzdem. Warum also nicht einfach eine Lösung wählen, die dieses X gut aktualisieren kann? Daher kann hier die Genetik direkt auf Pbest und Gbest angewendet und dann entsprechend einem bestimmten Gewicht „gelernt“ werden. Auf diese Weise hat dieses V eine „Eigenschaft“ von Pbest und Gbest. Wenn das also der Fall ist, kann ich dann nicht einige entsprechende „Merkmale“ lernen, wenn ich genetisches Crossover direkt nachahme und es mit Best kreuze?
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return pathGleichzeitig können wir immer noch Mutationen einführen.
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return pathVollständiger Code
ok, jetzt sehen wir uns den vollständigen Code an:
import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
def __init__(self ,data ,num_pop=200):
self.num_pop = num_pop # 群体个数
self.data = data # 城市坐标
self.num =len(data) # 城市个数
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离,我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()
def __matrix_dis(self):
"""
计算14个城市的距离,将这些距离用矩阵存起来
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path
def comp_fit(self, one_path):
"""
计算,咱们这个路径的长度,例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def init_population(self):
"""
初始化种群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.num_pop):
np.random.shuffle(rand_ch)
self.population[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
Path_short = HybridPsoTSP(data, num_pop=num_pop) # 混合粒子群算法类
Path_short.init_population() # 初始化种群
# 初始化路径绘图
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.population[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色体的路程: ' + str(Path_short.fitness[0]))
# 存储个体极值的路径和距离
best_P_population = Path_short.population.copy()
best_P_fit = Path_short.fitness.copy()
min_index = np.argmin(Path_short.fitness)
# 存储当前种群极值的路径和距离
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 存储每一步迭代后的最优路径和距离
best_population = [best_G_population]
best_fit = [best_G_fit]
# 复制当前群体进行交叉变异
x_new = Path_short.population.copy()
for i in range(max_n):
# 更新当前的个体极值
for j in range(num_pop):
if Path_short.fitness[j] < best_P_fit[j]:
best_P_fit[j] = Path_short.fitness[j]
best_P_population[j, :] = Path_short.population[j, :]
# 更新当前种群的群体极值
min_index = np.argmin(Path_short.fitness)
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 更新每一步迭代后的全局最优路径和解
if best_G_fit < best_fit[-1]:
best_fit.append(best_G_fit)
best_population.append(best_G_population)
else:
best_fit.append(best_fit[-1])
best_population.append(best_population[-1])
# 将每个个体与个体极值和当前的群体极值进行交叉
for j in range(num_pop):
# 与个体极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
fit = Path_short.comp_fit(x_new[j, :])
# 判断是否保留
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 与当前极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
fit = Path_short.comp_fit(x_new[j, :])
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 变异
x_new[j, :] = Path_short.mutation(x_new[j, :])
fit = Path_short.comp_fit(x_new[j, :])
if fit <= Path_short.fitness[j]:
Path_short.population[j] = x_new[j, :]
Path_short.fitness[j] = fit
if (i + 1) % 20 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
print('第' + str(i + 1) + '步后的最优路径:')
Path_short.out_path(Path_short.population[min_index, :]) # 显示每一步的最优路径
Path_short.best_population = best_population
Path_short.best_fit = best_fit
return Path_short # 返回结果类
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)初始染色体的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
可以看到收敛速度还是很快的。
特点分析
ok,到目前为止的话,我们介绍了两个算法去解决TSP或者是优化问题。我们来分析一下,这些算法有什么特点,为啥可以达到我们需要的优化效果。其实不管是遗传还是PSO,你其实都可以发现,有一个东西,我们可以暂且叫它环境压力。我们通过物竞天择,或者鸟类迁移,进行模拟寻优。而之所以需要这样做,是因为我们指定了一个规则,在我们的规则之下。我们让模拟的种群有一种压力去靠拢,其中物竞天择和鸟类迁移只是我们的一种手段,去应对这样的“压力”。所以的对于这种算法而言,最核心的点就两个:
设计环境压力
我们需要做优化问题,所以我们必须要能够让我们的解往那个方向走,需要一个驱动,需要一个压力。因此我们需要设计这样的一个环境,在遗传算法,粒子群算法是通过种群当中的生存,来进行设计的它的压力是我们的目标函数。由种群和目标函数(目标指标)构成了一个环境和压力。
设计压力策略
之后的话,我们设计好了一个环境和压力,那么未来应对这种压力,我们需要去设计一种策略,来应付这种压力。遗传算法是通过PUA自己,也就是种群的优胜略汰。PSO是通过学习,学习种群的优秀粒子和过去自己家的优秀“祖先”来应对这种压力的。
强化学习
所以的话,我们是否可以使用别的方案来实现这种优化效果。,在强化学习的算法框架里面的话,我们明确的知道了为什么他们可以实现优化,是环境压力+压力策略。恰好咱们强化学习是有环境的,适应函数和环境恰好可以组成环境+压力。本身的算法收敛过程就是我们的压力策略。所以我们完全是可以直接使用强化学习进行这个处理的。那么在这里咱们就来使用强化学习在下一篇文章当中。
Das obige ist der detaillierte Inhalt vonWie implementiert man mit Python den PSO-Algorithmus zur Lösung des TSP-Problems?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Muss MySQL bezahlen?
Apr 08, 2025 pm 05:36 PM
Muss MySQL bezahlen?
Apr 08, 2025 pm 05:36 PM
MySQL hat eine kostenlose Community -Version und eine kostenpflichtige Enterprise -Version. Die Community -Version kann kostenlos verwendet und geändert werden, die Unterstützung ist jedoch begrenzt und für Anwendungen mit geringen Stabilitätsanforderungen und starken technischen Funktionen geeignet. Die Enterprise Edition bietet umfassende kommerzielle Unterstützung für Anwendungen, die eine stabile, zuverlässige Hochleistungsdatenbank erfordern und bereit sind, Unterstützung zu bezahlen. Zu den Faktoren, die bei der Auswahl einer Version berücksichtigt werden, gehören Kritikalität, Budgetierung und technische Fähigkeiten von Anwendungen. Es gibt keine perfekte Option, nur die am besten geeignete Option, und Sie müssen die spezifische Situation sorgfältig auswählen.
 So verwenden Sie MySQL nach der Installation
Apr 08, 2025 am 11:48 AM
So verwenden Sie MySQL nach der Installation
Apr 08, 2025 am 11:48 AM
Der Artikel führt den Betrieb der MySQL -Datenbank vor. Zunächst müssen Sie einen MySQL -Client wie MySQLworkBench oder Befehlszeilen -Client installieren. 1. Verwenden Sie den Befehl mySQL-uroot-P, um eine Verbindung zum Server herzustellen und sich mit dem Stammkonto-Passwort anzumelden. 2. Verwenden Sie die Erstellung von Createdatabase, um eine Datenbank zu erstellen, und verwenden Sie eine Datenbank aus. 3.. Verwenden Sie CreateTable, um eine Tabelle zu erstellen, Felder und Datentypen zu definieren. 4. Verwenden Sie InsertInto, um Daten einzulegen, Daten abzufragen, Daten nach Aktualisierung zu aktualisieren und Daten nach Löschen zu löschen. Nur indem Sie diese Schritte beherrschen, lernen, mit gemeinsamen Problemen umzugehen und die Datenbankleistung zu optimieren, können Sie MySQL effizient verwenden.
 Die MySQL -Download -Datei ist beschädigt und kann nicht installiert werden. Reparaturlösung
Apr 08, 2025 am 11:21 AM
Die MySQL -Download -Datei ist beschädigt und kann nicht installiert werden. Reparaturlösung
Apr 08, 2025 am 11:21 AM
Die MySQL -Download -Datei ist beschädigt. Was soll ich tun? Wenn Sie MySQL herunterladen, können Sie die Korruption der Datei begegnen. Es ist heutzutage wirklich nicht einfach! In diesem Artikel wird darüber gesprochen, wie dieses Problem gelöst werden kann, damit jeder Umwege vermeiden kann. Nach dem Lesen können Sie nicht nur das beschädigte MySQL -Installationspaket reparieren, sondern auch ein tieferes Verständnis des Download- und Installationsprozesses haben, um zu vermeiden, dass Sie in Zukunft stecken bleiben. Lassen Sie uns zunächst darüber sprechen, warum das Herunterladen von Dateien beschädigt wird. Dafür gibt es viele Gründe. Netzwerkprobleme sind der Schuldige. Unterbrechung des Download -Prozesses und der Instabilität im Netzwerk kann zu einer Korruption von Dateien führen. Es gibt auch das Problem mit der Download -Quelle selbst. Die Serverdatei selbst ist gebrochen und natürlich auch unterbrochen, wenn Sie sie herunterladen. Darüber hinaus kann das übermäßige "leidenschaftliche" Scannen einer Antiviren -Software auch zu einer Beschädigung von Dateien führen. Diagnoseproblem: Stellen Sie fest, ob die Datei wirklich beschädigt ist
 MySQL kann nach dem Herunterladen nicht installiert werden
Apr 08, 2025 am 11:24 AM
MySQL kann nach dem Herunterladen nicht installiert werden
Apr 08, 2025 am 11:24 AM
Die Hauptgründe für den Fehler bei MySQL -Installationsfehlern sind: 1. Erlaubnisprobleme, Sie müssen als Administrator ausgeführt oder den Sudo -Befehl verwenden. 2. Die Abhängigkeiten fehlen, und Sie müssen relevante Entwicklungspakete installieren. 3. Portkonflikte müssen Sie das Programm schließen, das Port 3306 einnimmt, oder die Konfigurationsdatei ändern. 4. Das Installationspaket ist beschädigt. Sie müssen die Integrität herunterladen und überprüfen. 5. Die Umgebungsvariable ist falsch konfiguriert und die Umgebungsvariablen müssen korrekt entsprechend dem Betriebssystem konfiguriert werden. Lösen Sie diese Probleme und überprüfen Sie jeden Schritt sorgfältig, um MySQL erfolgreich zu installieren.
 Lösungen für den Dienst, der nach der MySQL -Installation nicht gestartet werden kann
Apr 08, 2025 am 11:18 AM
Lösungen für den Dienst, der nach der MySQL -Installation nicht gestartet werden kann
Apr 08, 2025 am 11:18 AM
MySQL hat sich geweigert, anzufangen? Nicht in Panik, lass es uns ausprobieren! Viele Freunde stellten fest, dass der Service nach der Installation von MySQL nicht begonnen werden konnte, und sie waren so ängstlich! Mach dir keine Sorgen, dieser Artikel wird dich dazu bringen, ruhig damit umzugehen und den Mastermind dahinter herauszufinden! Nachdem Sie es gelesen haben, können Sie dieses Problem nicht nur lösen, sondern auch Ihr Verständnis von MySQL -Diensten und Ihren Ideen zur Fehlerbehebungsproblemen verbessern und zu einem leistungsstärkeren Datenbankadministrator werden! Der MySQL -Dienst startete nicht und es gibt viele Gründe, von einfachen Konfigurationsfehlern bis hin zu komplexen Systemproblemen. Beginnen wir mit den häufigsten Aspekten. Grundkenntnisse: Eine kurze Beschreibung des Service -Startup -Prozesses MySQL Service Startup. Einfach ausgedrückt, lädt das Betriebssystem MySQL-bezogene Dateien und startet dann den MySQL-Daemon. Dies beinhaltet die Konfiguration
 Braucht MySQL das Internet?
Apr 08, 2025 pm 02:18 PM
Braucht MySQL das Internet?
Apr 08, 2025 pm 02:18 PM
MySQL kann ohne Netzwerkverbindungen für die grundlegende Datenspeicherung und -verwaltung ausgeführt werden. Für die Interaktion mit anderen Systemen, Remotezugriff oder Verwendung erweiterte Funktionen wie Replikation und Clustering ist jedoch eine Netzwerkverbindung erforderlich. Darüber hinaus sind Sicherheitsmaßnahmen (wie Firewalls), Leistungsoptimierung (Wählen Sie die richtige Netzwerkverbindung) und die Datensicherung für die Verbindung zum Internet von entscheidender Bedeutung.
 Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Die MySQL-Datenbankleistung Optimierungshandbuch In ressourcenintensiven Anwendungen spielt die MySQL-Datenbank eine entscheidende Rolle und ist für die Verwaltung massiver Transaktionen verantwortlich. Mit der Erweiterung der Anwendung werden jedoch die Datenbankleistung Engpässe häufig zu einer Einschränkung. In diesem Artikel werden eine Reihe effektiver Strategien zur Leistungsoptimierung von MySQL -Leistung untersucht, um sicherzustellen, dass Ihre Anwendung unter hohen Lasten effizient und reaktionsschnell bleibt. Wir werden tatsächliche Fälle kombinieren, um eingehende Schlüsseltechnologien wie Indexierung, Abfrageoptimierung, Datenbankdesign und Caching zu erklären. 1. Das Design der Datenbankarchitektur und die optimierte Datenbankarchitektur sind der Eckpfeiler der MySQL -Leistungsoptimierung. Hier sind einige Kernprinzipien: Die Auswahl des richtigen Datentyps und die Auswahl des kleinsten Datentyps, der den Anforderungen entspricht, kann nicht nur Speicherplatz speichern, sondern auch die Datenverarbeitungsgeschwindigkeit verbessern.
 So optimieren Sie die Datenbankleistung nach der MySQL -Installation
Apr 08, 2025 am 11:36 AM
So optimieren Sie die Datenbankleistung nach der MySQL -Installation
Apr 08, 2025 am 11:36 AM
Die MySQL -Leistungsoptimierung muss von drei Aspekten beginnen: Installationskonfiguration, Indexierung und Abfrageoptimierung, Überwachung und Abstimmung. 1. Nach der Installation müssen Sie die my.cnf -Datei entsprechend der Serverkonfiguration anpassen, z. 2. Erstellen Sie einen geeigneten Index, um übermäßige Indizes zu vermeiden und Abfrageanweisungen zu optimieren, z. B. den Befehl Erklärung zur Analyse des Ausführungsplans; 3. Verwenden Sie das eigene Überwachungstool von MySQL (ShowProcessList, Showstatus), um die Datenbankgesundheit zu überwachen und die Datenbank regelmäßig zu sichern und zu organisieren. Nur durch kontinuierliche Optimierung dieser Schritte kann die Leistung der MySQL -Datenbank verbessert werden.



