Methoden und Schritte zur Implementierung der Monte-Carlo-Simulation in Python

Was ist Monte-Carlo-Simulation? Wahrscheinlichkeit, dass ein Ereignis eintritt. Im Projektmanagement wird die Monte-Carlo-Simulation hauptsächlich zur Berechnung der Wahrscheinlichkeitsverteilung von Schlüsselindikatoren wie Projektdauer und -kosten verwendet und hilft Projektmanagern, Risiken besser zu verwalten und Entscheidungen zu treffen.

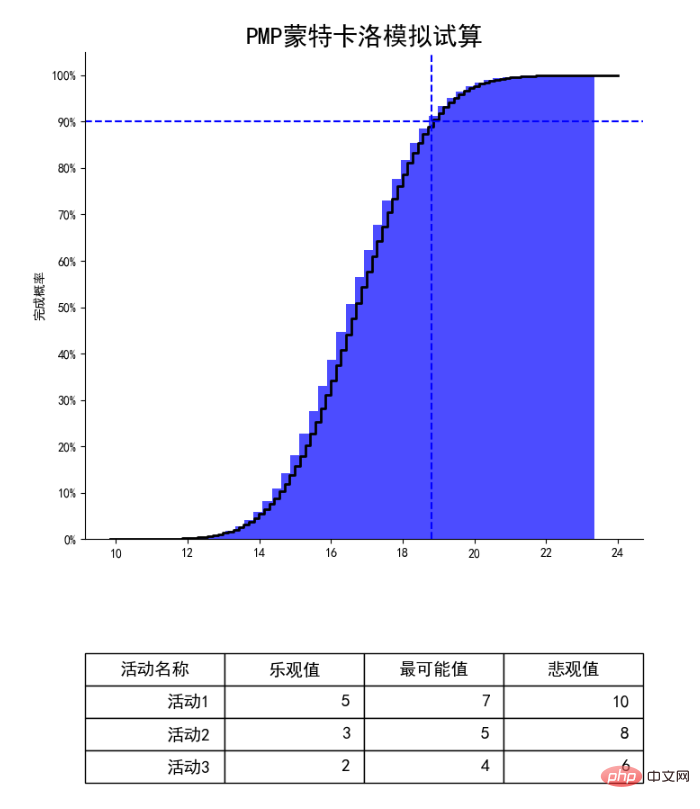
Sehen wir uns das Bild oben an. Dieses Bild ist eine Monte-Carlo-Simulation für drei Projektaktivitäten: Aktivität 1, Aktivität 2 und Aktivität 3. Die Simulation basiert auf Dreipunktschätzungen der drei Aktivitäten. Dann wurde der Computer aufgefordert, 1.000.000 Mal zufällige Budgets auszuführen, und das obige Bild wurde erhalten.

Nehmen wir als Beispiel den Schnittpunkt der blauen gepunkteten Linien im Bild oben. Worauf bezieht sich dieser Punkt? Schauen wir uns die Y-Achse an. Die 90 % beziehen sich hier auf die 90 %ige Abschlusswahrscheinlichkeit. Die diesem Punkt entsprechende horizontale Achse liegt nahe bei 19 Tagen. Mit anderen Worten, durch Computersimulation 1 Million Mal. Die Wahrscheinlichkeit, das Projekt in weniger als 19 Tagen abzuschließen, liegt bei 90 %.

Studenten, die Projekte durchgeführt haben, wissen alle, dass Kunden oder Führungskräfte immer möchten, dass wir immer schneller werden. Der Anführer sagte, es gebe keine 19 Tage, sondern nur 16 Tage. Zu diesem Zeitpunkt habe ich als Projektmanager anhand der obigen Grafik festgestellt, dass der Wert der X-Achse, der der Y-Achse entspricht, für 16 Tage etwa 30 % beträgt. Fragen Sie einfach den Leiter: Die Erfolgsquote beträgt nur 30 %. Wollen Sie wetten oder nicht? Das ist eine gute Art der „wissenschaftlichen Wahrsagerei“. Der Schlüssel liegt in der Einfachheit und der Wahrscheinlichkeitstheorie als Stütze.

Python-Implementierung

Wie berechnet man die Monte-Carlo-Simulation des Projektmanagements in Python? Es ist eigentlich ganz einfach. Wir können die Numpy- und Matplotlib-Bibliotheken in Python verwenden, um Berechnungen und Zeichnungen durchzuführen. Lehrer Tian gibt unten den vollständigen Code an:

#!/usr/bin/env python
# -*- coding:utf-8 -*-
"""
#-----------------------------------------------------------------------------
#                     --- TDOUYA STUDIOS ---
#-----------------------------------------------------------------------------
#
# @Project : di08-tdd-cdg-python-learning
# @File    : monte_carlo.py
# @Author  : tianxin.xp@gmail.com
# @Date    : 2023/3/12 18:22
#
# 用Python实现蒙特卡洛模拟
#
#--------------------------------------------------------------------------"""
from datetime import datetime

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter, MultipleLocator
from scipy.stats import norm

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def to_percent(y, position):
    # 将纵轴用百分数表示
    return '{:.0f}%'.format(100 * y)


class Activity:
    """ 活动类，用于表示一个项目中的活动

   Attributes:
       name (str): 活动名称
       optimistic (float): 乐观时间
       pessimistic (float): 悲观时间
       most_likely (float): 最可能时间
   """

    def __init__(self, name, optimistic, pessimistic, most_likely):
        """
            初始化活动类

            Args:
                name (str): 活动名称
                optimistic (float): 乐观时间
                pessimistic (float): 悲观时间
                most_likely (float): 最可能时间
        """
        self.name = name
        self.optimistic = optimistic
        self.pessimistic = pessimistic
        self.most_likely = most_likely


class PMP:
    """
    PMP类用于进行项目管理中的相关计算：
    方法：
    monte_carlo_simulation : 蒙特卡洛模拟试算，包括计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等功能。
    """

    def __init__(self, activities):
        """
        初始化PMP类，传入活动列表。
        :param activities: 活动列表，包括活动名称、乐观值、最可能值和悲观值。
        """
        self.activities = activities

    def monte_carlo_simulation(self, n):
        """
        进行蒙特卡洛模拟试算，计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等。
        :param n: 模拟次数。
        """
        # 模拟参数和变量
        t = []
        for activity in self.activities:
            t.append(np.random.triangular(activity.optimistic, activity.most_likely, activity.pessimistic, n))

        # 计算项目工期
        project_duration = sum(t)

        # 计算平均值和标准差
        mean_duration = np.mean(project_duration)
        std_duration = np.std(project_duration)

        # 绘制积累图
        fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 10), gridspec_kw={'height_ratios': [3, 1]})

        ax1.hist(project_duration, bins=50, density=True, alpha=0.7, color='blue', cumulative=True)
        ax1.yaxis.set_major_locator(MultipleLocator(0.1))
        ax1.yaxis.set_major_formatter(FuncFormatter(to_percent))
        ax1.set_ylabel('完成概率')
        ax1.set_title('PMP蒙特卡洛模拟试算', fontsize=20)

        # 绘制概率密度曲线
        xmin, xmax = ax1.get_xlim()
        x = np.linspace(xmin, xmax, 100)
        p = norm.cdf(x, mean_duration, std_duration)
        ax1.plot(x, p, 'k', linewidth=2, drawstyle='steps-post')

        # 找到完成概率90%的点
        x_90 = norm.ppf(0.9, mean_duration, std_duration)

        # 绘制垂线
        ax1.axvline(x_90, linestyle='--', color='blue')
        ax1.axhline(0.9, linestyle='--', color='blue')

        # 隐藏右边和上方的坐标轴线
        ax1.spines['right'].set_visible(False)
        ax1.spines['top'].set_visible(False)

        # 添加表格
        col_labels = ['活动名称', '乐观值', '最可能值', '悲观值']

        cell_text = [[activity.name, activity.optimistic, activity.most_likely, activity.pessimistic] for activity in
                     self.activities]
        table = ax2.table(cellText=cell_text, colLabels=col_labels, loc='center')

        # 设置表格的字体大小和行高
        table.auto_set_font_size(False)
        table.set_fontsize(14)

        # # 设置表格的行高为1.5倍原来的高度
        for i in range(len(self.activities) + 1):
            table._cells[(i, 0)].set_height(0.2)
            table._cells[(i, 1)].set_height(0.2)
            table._cells[(i, 2)].set_height(0.2)
            table._cells[(i, 3)].set_height(0.2)

        ax2.axis('off')

        # 调整子图之间的间距和边距
        plt.subplots_adjust(hspace=0.3, bottom=0.05)

        # 保存图表
        now = datetime.now().strftime('%Y%m%d%H%M%S')
        plt.savefig('monte_carlo_simulation_{}.png'.format(now))

        # 显示图形
        plt.show()


if __name__ == '__main__':
    # 模拟参数和变量
    n = 1000000  # 模拟次数

    # 活动的工期分布
    activities = [
        Activity('活动1', 5, 10, 7),
        Activity('活动2', 3, 8, 5),
        Activity('活动3', 2, 6, 4)
    ]

    # 进行蒙特卡洛模拟
    pmp = PMP(activities)
    pmp.monte_carlo_simulation(n)

Das obige ist der detaillierte Inhalt vonMethoden und Schritte zur Implementierung der Monte-Carlo-Simulation in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!