Wie sortiere ich 100 Millionen Zufallszahlen in Java?

1. Direkte Einfügungssortierung

1. Illustrierte Einfügungssortierung

Idee: Im wahrsten Sinne des Wortes bedeutet Einfügung, ein Element gemäß einer bestimmten Regel in einen bestimmten Satz einzufügen, daher müssen wir die Sequenz in zwei Teile, einen Teil, aufteilen ist ein geordneter Satz, und der andere Teil ist der zu sortierende Satz Ideen, wir müssen die Sequenz in zwei Teile umwandeln. Zur Vereinfachung der Codierung gehen wir davon aus, dass das erste Element eine geordnete Menge ist. Dann sollte unsere Schleife

beim 2. Element

beginnen, also 3, um ein Überschreiben zu vermeiden 3. In nachfolgenden Operationen wählen wir eine temporäre Variable aus, um 3 zu speichern. Das ist der obige val=arr[1],

Da wir das Array bearbeiten, müssen wir auch die 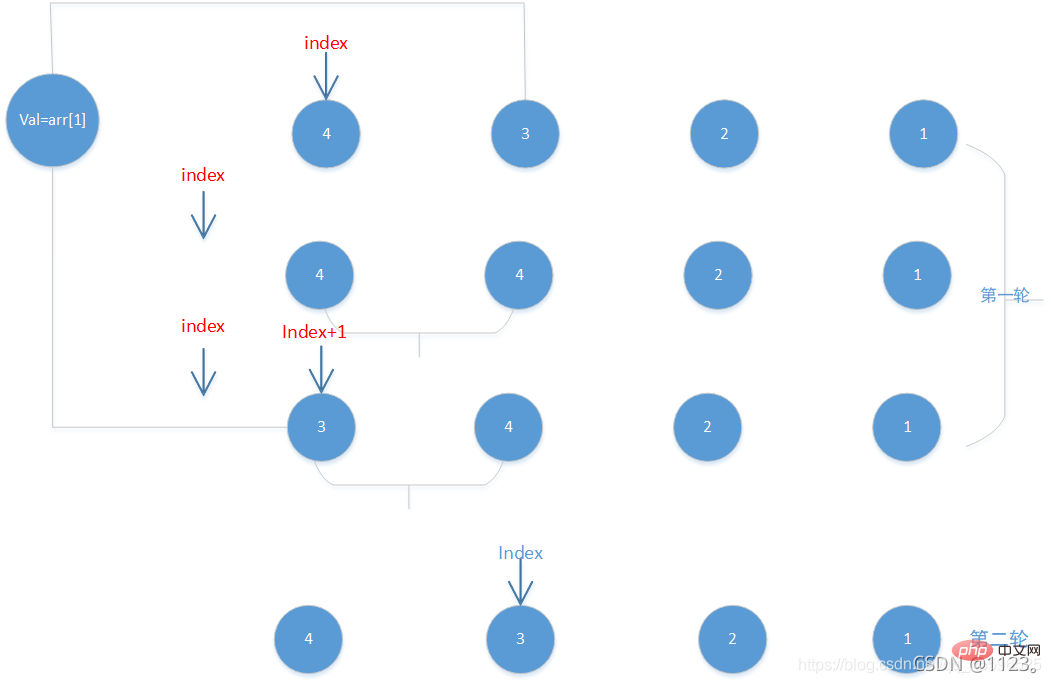ordered erhalten set Der Index des letzten Elements wird als Cursor verwendet

Wenn der Cursor

die Grenze nicht überschreitet und der einzufügende Wert kleiner ist als die vom Cursor angegebene Position (4 im Bild oben) verschieben wir Element 4 nach hinten. Der Cursor bewegt sich vorwärts und prüft weiter, ob andere Elemente im Satz kleiner sind als das einzufügende Element, bis der Cursor die Grenze im Bild oben überschreitet, da diese vorhanden ist Nur eine 4 im Satz, der Cursor bewegt sich vorwärts und überschreitet die Grenze, sodass die nächste Vergleichsrunde beginnt

2. Leistungstests und Raum-Zeit-Komplexität

val=arr[1] ,

由于是对数组继进行操作 , 我们同时也需要获取有序集合的最后一个元素的索引作为游标

当游标不越界 , 且待插入的值小于游标指示位置时(上图的4) , 我们将元素4后移 , 游标前移,继续检查集合中的其它元素是否也小于待插入的元素, 直到游标越界

上图由于集合内只有一个4, 游标前移越界了, 因此循环终止. 下一轮比较开始执行

2. 代码实现

public static void insertSort(int[]arr){
        for(int i = 1 ; i < arr.length; i++){
            int val = arr[i];
            int valIndex = i - 1; //游标
            while(valIndex >= 0 && val < arr[valIndex]){ //插入的值比游标指示的值小
                arr[valIndex + 1] = arr[valIndex];
                valIndex--; //游标前移
            }
            arr[valIndex+1] = val;
        }
    }
1234567891011

3.性能检测与时空复杂度

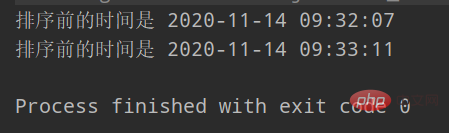
实际运行80w个数据耗时1分4秒(非准确值,每台机器可能都不一样)

直接插排在排序记录较少, 关键字基本有序的情况下效率较高

时间复杂度 :

关键字比较次数 : KCN=(n^2)/2 总移动次数 : RMN= (n^2)/2

因此时间复杂度约为 O(N^2)

二、希尔排序(交换法)

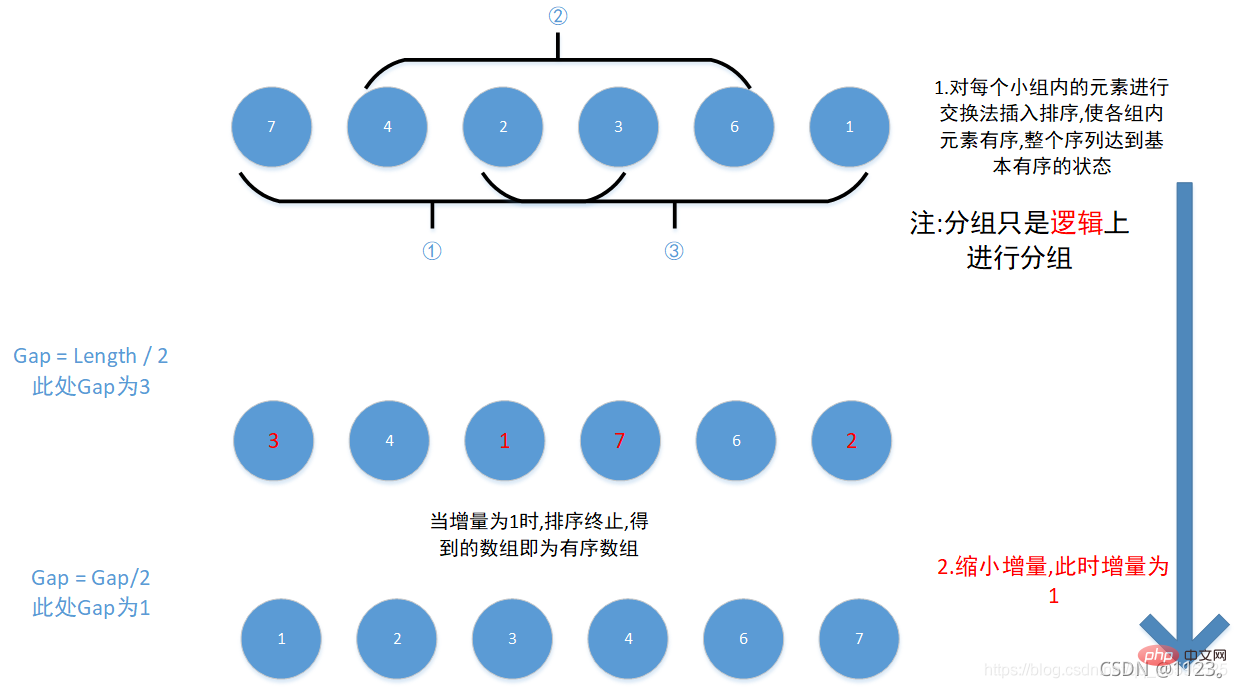
1. 思路图解

2. 代码实现

public static void shellSort(int[] arr){ //交换法
        int tmp = 0;
        for(int gap = arr.length / 2 ; gap > 0 ; gap /= 2){
            for(int i = gap ; i < arr.length ; i++){ //先遍历所有数组
                for(int j  = i - gap ; j >= 0 ; j -= gap){//开启插入排序
                    if(arr[ j ] > arr[ gap + j ]){ //可以根据升降序修改大于或小于
                        tmp = arr[gap + j];
                        arr[j+gap] = arr[j];
                        arr[j] = tmp;
                    }
                }
            }
            System.out.println(gap);
            System.out.println(Arrays.toString(arr));
        }
    }
12345678910111213141516

这里最难理解的应该是第三个for循环,j = i - gap, 表示小组内的第一个元素,即j=0,

当小组内的第一个元素大于第二个元素时(由于是逻辑上的分类,第二个元素的索引应当是第一个元素的所有值+增量gap) , 交换两者,反之j-=gap,继续比较或跳出循环 ,

如此往复将所有小组都遍历完之后 , 缩小增量(即gap/=2) , 然后继续上述步骤, 直到增量gap为1时, 序列排序结束

3. 时间复杂度

希尔排序的时间复杂度取决于增量序列的函数 , 需要具体问题具体分析,并不是一个确定的值,这也是第四点需要讨论的问题

4. 关于增量的选择

上述我们在做排序的时候增量缩减选用的时gap/=2的模型, 这并不是最优的选择 , 关于增量的选取 , 属于数学界尚未解决的一个问题

但是可以确定的是, 通过大量的实验证明 ,当n->无穷大Es dauert 1 Minute und 4 Sekunden, um 800.000 Daten auszuführen (kein genauer Wert, jede Maschine kann anders sein)

Es gibt weniger Datensätze beim direkten Einfügen und Sortieren, Schlüsselwörter Die Effizienz ist höher, wenn sie grundsätzlich geordnet ist

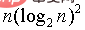
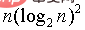
Zeitliche Komplexität:

Anzahl Schlüsselwortvergleiche: KCN=(n^2)/2 Gesamtzahl der Züge: RMN= ( n^2)/2

Bei der Zeitkomplexität geht es also um O(N^2)

2. Hill-Sortierung (Austauschmethode)

1. Illustration von Ideen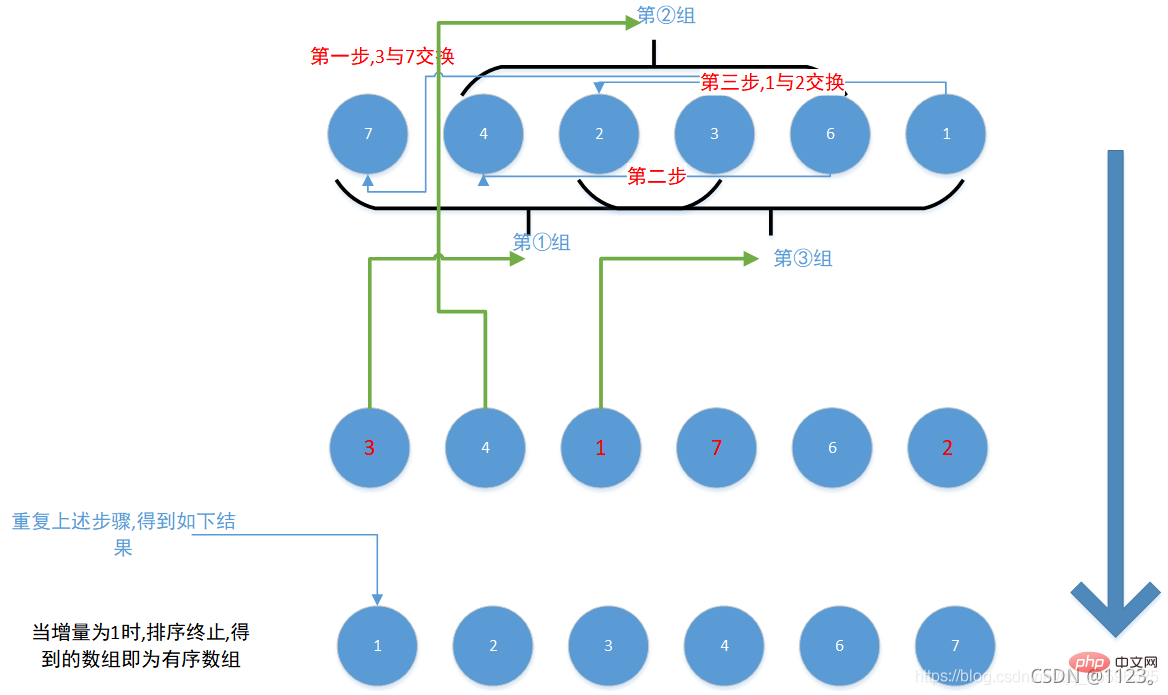

2. Code-Implementierung

public static void shellSort02(int[] arr){ //移位法
        for(int gap = arr.length/2 ; gap > 0 ; gap /= 2){ //分组
            for(int i = gap ; i < arr.length ; i++){ //遍历
                int valIndex = i;
                int val = arr[valIndex];
                if(val < arr[valIndex-gap]){ //插入的值小于组内另一个值
                   while(valIndex - gap >=0 && val < arr[valIndex-gap]){ //开始插排
                       // 插入
                       arr[valIndex] = arr[valIndex-gap];
                       valIndex -= gap; //让valIndex = valIndex-gap (游标前移)
                   }
                }
                arr[valIndex] = val;
            }
        }
    }
12345678910111213141516

Am schwierigsten zu verstehen ist hier wahrscheinlich die dritte for-Schleife, j = i - Lücke, das das erste Element in der Gruppe darstellt, also j=0, Wenn das erste Element in der Gruppe größer als das zweite Element ist (

Aufgrund der logischen Klassifizierung sollte der Index des zweiten Elements alle Werte des ersten Elements + die inkrementelle Lücke sein), die beiden austauschen, andernfalls j-=gap, weitermachen Um zu vergleichen oder aus der Schleife zu springen,

Nachdem alle Gruppen auf diese Weise durchlaufen wurden, reduzieren Sie das Inkrement (d. h. gap/=2) und fahren Sie dann mit den obigen Schritten fort, bis die inkrementelle Lücke 1 beträgt , und die Sequenzsortierung endet

3. Zeitkomplexität

Die zeitliche Komplexität der Hill-Sortierung hängt von der Funktion der inkrementellen Sequenz ab, die eine spezifische Analyse spezifischer Probleme erfordert und nicht derselbe ist Vierter Punkt, der besprochen werden muss

4. In Bezug auf die Wahl des Inkrements

Als wir die obige Sortierung durchgeführt haben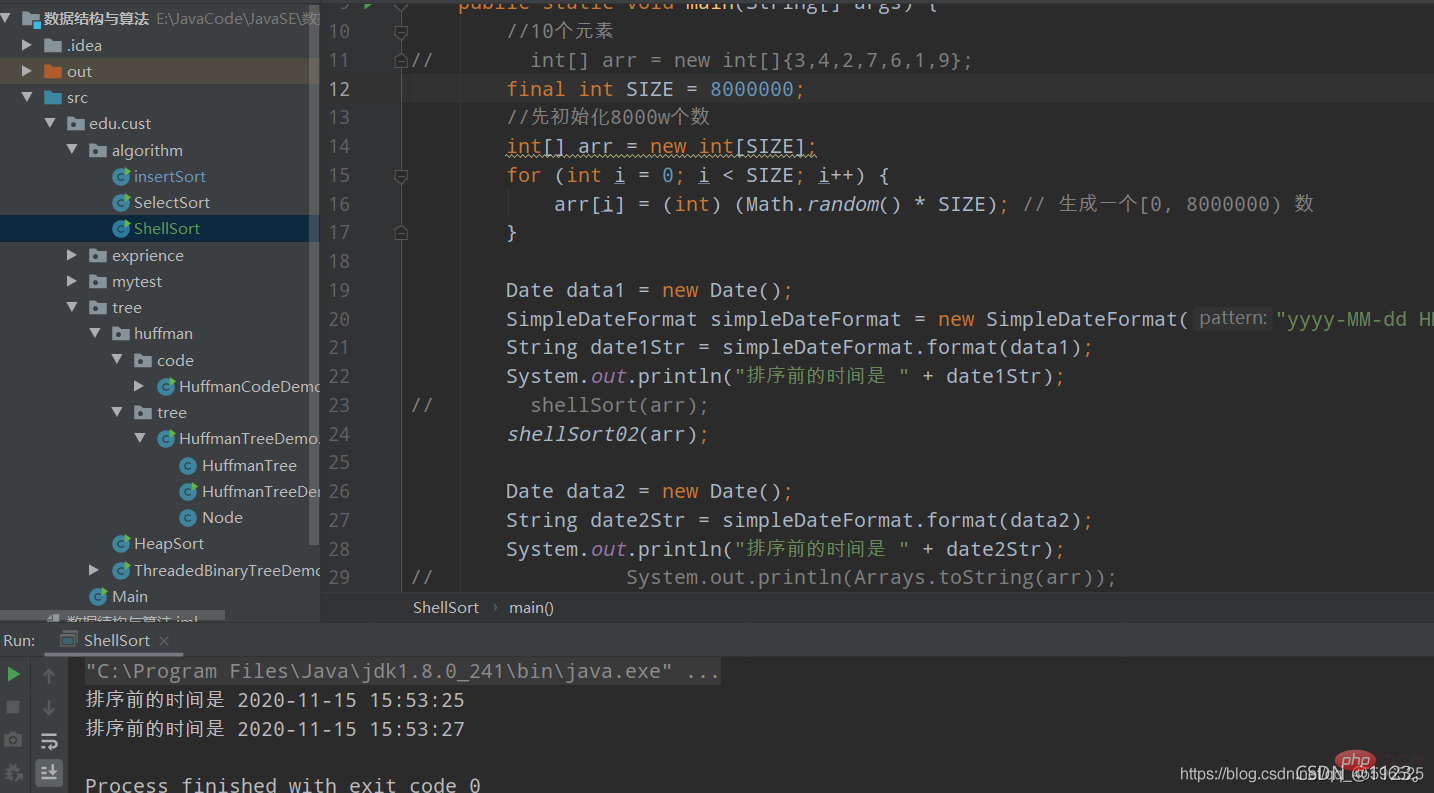inkrementelle Reduzierung
Als wir das Modell gap/=2 gewählt haben, ist dies nicht die optimale Wahl . Die Auswahl von Inkrementen ist ein ungelöstes Problem in der mathematischen Gemeinschaft.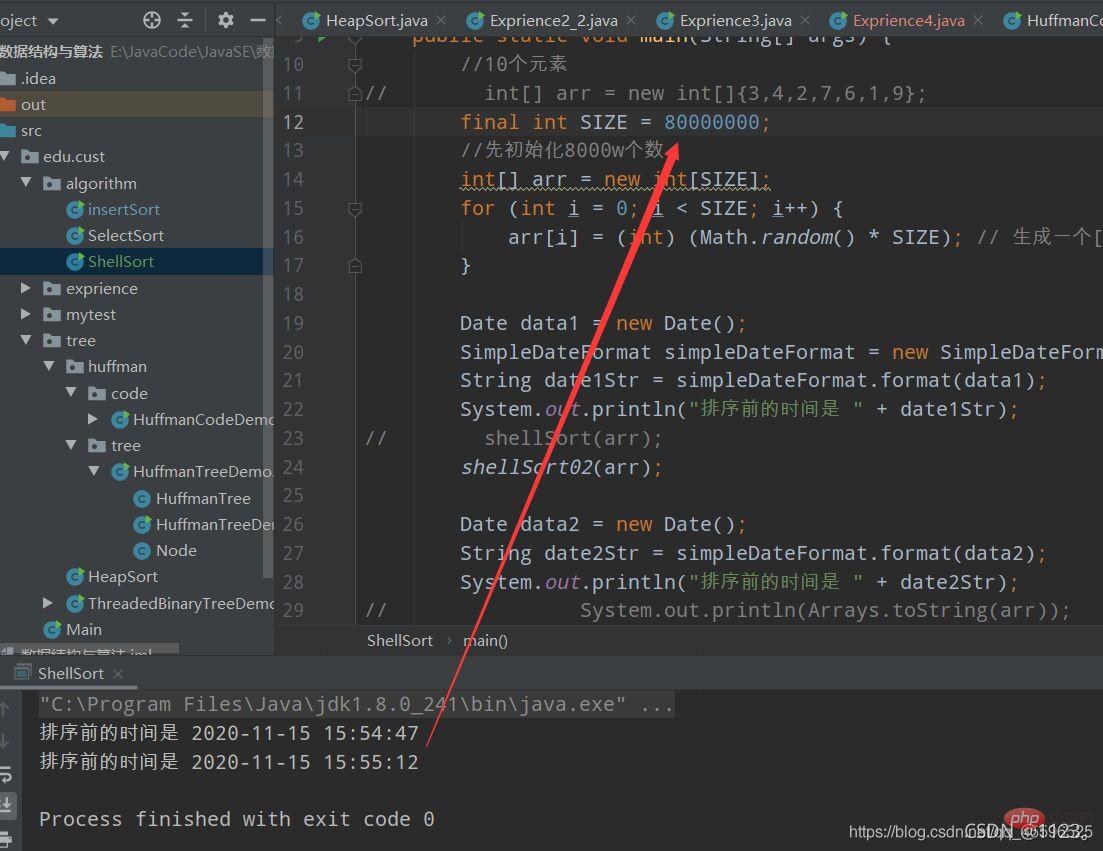
Sicher ist jedoch, dass durch eine große Anzahl von Experimenten bewiesen wurde, dass bei n->unendlich code> die Zeitkomplexität zunimmt kann reduziert werden auf: <img src="https://img.php.cn/upload/article/000/887/227/168362467311513.png" alt="Wie sortiere ich 100 Millionen Zufallszahlen in Java?">

🎜🎜🎜Im nächsten Punkt, 🎜Verschiebungsmethode🎜, haben wir auch mehrere Experimente durchgeführt und können sicher sein, dass für einen bestimmten Maßstab (z. B. 800 W ~ 100 Millionen) in Bezug auf die Berechnung 🎜Hill-Sortierung ist viel schneller als Heap-Sortierung🎜, zumindest auf meinem Computer 🎜🎜3. Hill-Sortierung (Shift-Methode)🎜🎜Die Austauschmethode ist viel langsamer als die Shift-Methode, daher wird die 🎜Shift-Methode🎜 häufiger verwendet , und die Verschiebungsmethode ähnelt eher der Einfügungssortierung 🎜🎜1. Die Idee 🎜🎜Die Idee ist eigentlich eine Kombination der beiden oben genannten Sortiermethoden, Gruppierung 🎜 in Gruppen🎜 In Kombination mit den Vorteilen von 🎜Einfügung🎜 ist die Effizienz sehr hoch🎜🎜 verkörpert die Idee von 🎜Teile und herrsche🎜, eine größere Sequenz in mehrere kleinere Sequenzen zu zerlegen🎜🎜🎜🎜🎜2. Code-Implementierung🎜rrreee🎜3. Experimentelle Ergebnisse🎜🎜🎜🎜🎜🎜

Das obige ist der detaillierte Inhalt vonWie sortiere ich 100 Millionen Zufallszahlen in Java?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!