 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 So implementieren Sie den Hill-Sortieralgorithmus in Python
So implementieren Sie den Hill-Sortieralgorithmus in Python
So implementieren Sie den Hill-Sortieralgorithmus in Python
Algorithmusbeschreibung
Hill-Sortierung, auch „reduzierende inkrementelle Sortierung“ genannt, ist ein Sortieralgorithmus, der durch Optimierung der Einfügungssortierung erstellt wird. Seine Ausführungsidee besteht darin, die Elemente im Array in tiefgestellte Inkremente zu gruppieren, jede Gruppe von Elementen einzufügen und zu sortieren, das Inkrement zu reduzieren und die vorherigen Schritte zu wiederholen, bis das Inkrement 1 erreicht.
Im Allgemeinen beträgt die zeitliche Komplexität der Hill-Sortierung O(n1,3)~O(n2), was von der Inkrementgröße abhängt. Die räumliche Komplexität der Hill-Sortierung beträgt O(1), was ein instabiler Sortieralgorithmus ist. Bei der Hügelsortierung kann sich eine Bewegung eines Elements über mehrere Elemente erstrecken, was mehrere Bewegungen ausgleichen und die Effizienz verbessern kann.
Das Folgende ist eine aufsteigende Hill-Sortierung mit (Array-Länge/2) als anfänglichem Inkrement. Nach jeder Sortierrunde wird das Inkrement um die Hälfte reduziert.
Schritt eins:
Wie in Abbildung 2-28 gezeigt, gruppieren Sie ausgehend vom ersten Element nach Schritt 4. Es ist ersichtlich, dass bei einem Inkrement von 4 nur zwei Elemente in einer Gruppe vorhanden sind, andernfalls überschreitet der Index des Elements den Bereich des Arrays.
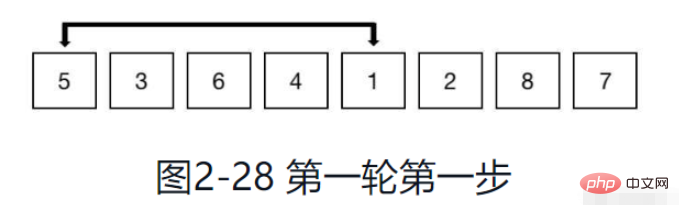
Schritt 2:
Führen Sie, wie in Abbildung 2-29 gezeigt, eine Einfügungssortierung für die Elemente in der Gruppe durch.
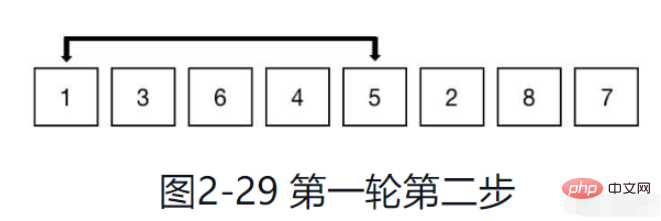
Schritt 3:
Wie in Abbildung 2-30 gezeigt, verwenden Sie weiterhin dieselbe Methode zum Gruppieren und fügen Sie die Elemente in die Gruppe ein und sortieren Sie sie, um sie zu ordnen.
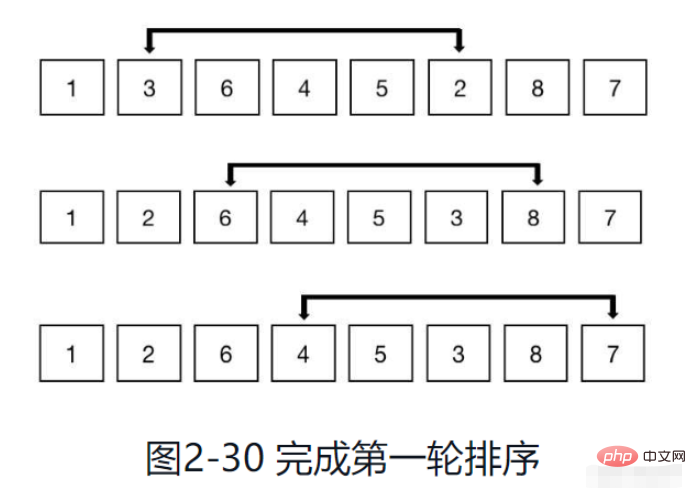
Nachdem alle Zahlen im gesamten Array durchlaufen wurden, ist diese Sortierrunde beendet. Reduzieren Sie die Schrittweite um die Hälfte und fahren Sie mit der nächsten Sortierrunde fort.
Schritt 4:
Wie in Abbildung 2-31 gezeigt, ist bei einem Inkrement von 2 ersichtlich, dass die Elemente in jeder Gruppe zugenommen haben und die Gesamtzahl der Gruppen abgenommen hat. Fahren Sie mit dem Einfügen und Sortieren der Elemente in jeder Gruppe fort, bis jede Gruppe durchlaufen ist.
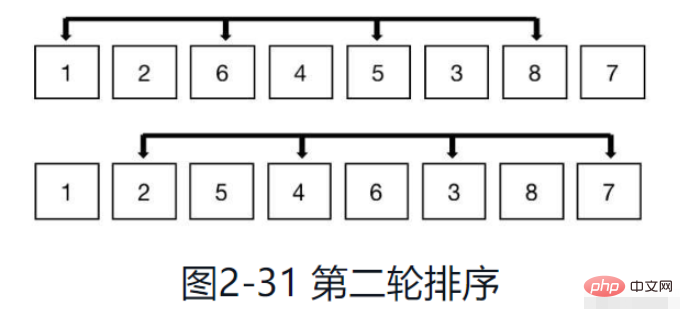
Schritt 5:
Die letzte Sortierrunde ist in Abbildung 2-32 dargestellt. Reduzieren Sie das Inkrement zu diesem Zeitpunkt erneut um 1, was der Einfügungssortierung des gesamten Arrays entspricht. Das heißt, die letzte Rundensortierung.
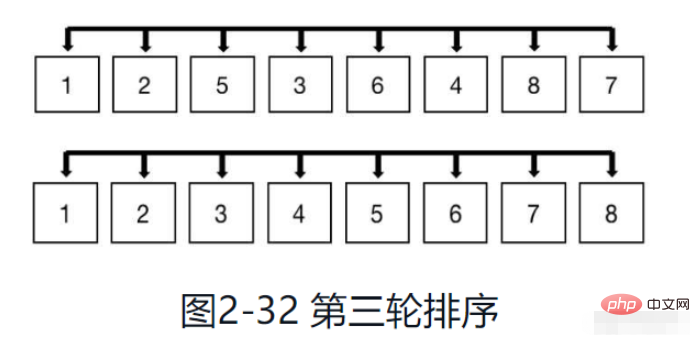
Nach der letzten Sortierrunde ist die gesamte Hügelsortierung beendet.
Code-Implementierung
Da in der for-Schleife das erste Element jeder Gruppe nicht eingefügt und sortiert werden muss und ihre Indizes zwischen 0 und Schritt-1 liegen, beginnt die Durchquerung ab dem Indexschritt.
Es ist zu beachten, dass Sie, wenn Sie den Ansatz im Flussdiagramm simulieren möchten, zwei Schleifen verwenden müssen: Zuerst gruppieren und dann die Elemente gleichzeitig in derselben Gruppe anordnen. Um die Effizienz zu verbessern, verwenden wir direkt eine for-Schleife. Jedes Mal, wenn eine Zahl durchlaufen wird, wird die Gruppe, in der sie sich befindet, eingefügt und sortiert. Dieser Durchlauf erfüllt auch die Reihenfolgeanforderungen der Einfügungssortierung. Bei der Einfügungssortierung muss der Wert des aktuellen Index geändert werden. Daher wird die Variable ind zum Speichern des aktuellen Index verwendet, um zu verhindern, dass er die for-Schleife beeinflusst.
Die gewöhnliche Einfügungssortierung entspricht der Hill-Sortierung mit einer Schrittweite von 1. Die Hill-Sortierung über Elemente hinweg ändert eigentlich nur die Schrittweite und unterscheidet sich logischerweise nicht von der gewöhnlichen Einfügungssortierung.
Hill-Sortiercode:
nums = [5,3,6,4,1,2,8,7]
def ShellSort(nums):
step = len(nums)//2 #初始化增量为数组长度的一半
while step > 0: #增量必须是大于0的整数
for i in range(step,len(nums)): #遍历需要进行插入排序的数
ind = i
while ind >= step and nums[ind] < nums[ind-step]: #对每组进行插入排序
nums[ind],nums[ind-step] = nums[ind-step],nums[ind]
ind -= step
step //= 2 #增量缩小一半
print(nums)
ShellSort(nums)Führen Sie das Programm aus. Das Ausgabeergebnis lautet:
[1,2,3,4,5,6,7,8]
Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Hill-Sortieralgorithmus in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Hadidb: Eine leichte, horizontal skalierbare Datenbank in Python
Apr 08, 2025 pm 06:12 PM
Hadidb: Eine leichte, horizontal skalierbare Datenbank in Python
Apr 08, 2025 pm 06:12 PM
Hadidb: Eine leichte, hochrangige skalierbare Python-Datenbank Hadidb (HadIDB) ist eine leichte Datenbank in Python mit einem hohen Maß an Skalierbarkeit. Installieren Sie HadIDB mithilfe der PIP -Installation: PipinstallHadIDB -Benutzerverwaltung erstellen Benutzer: createUser (), um einen neuen Benutzer zu erstellen. Die Authentication () -Methode authentifiziert die Identität des Benutzers. fromHadidb.operationImportUseruser_obj = user ("admin", "admin") user_obj.
 Python: Erforschen der primären Anwendungen
Apr 10, 2025 am 09:41 AM
Python: Erforschen der primären Anwendungen
Apr 10, 2025 am 09:41 AM
Python wird in den Bereichen Webentwicklung, Datenwissenschaft, maschinelles Lernen, Automatisierung und Skripten häufig verwendet. 1) In der Webentwicklung vereinfachen Django und Flask Frameworks den Entwicklungsprozess. 2) In den Bereichen Datenwissenschaft und maschinelles Lernen bieten Numpy-, Pandas-, Scikit-Learn- und TensorFlow-Bibliotheken eine starke Unterstützung. 3) In Bezug auf Automatisierung und Skript ist Python für Aufgaben wie automatisiertes Test und Systemmanagement geeignet.
 Der 2-stündige Python-Plan: ein realistischer Ansatz
Apr 11, 2025 am 12:04 AM
Der 2-stündige Python-Plan: ein realistischer Ansatz
Apr 11, 2025 am 12:04 AM
Sie können grundlegende Programmierkonzepte und Fähigkeiten von Python innerhalb von 2 Stunden lernen. 1. Lernen Sie Variablen und Datentypen, 2. Master Control Flow (bedingte Anweisungen und Schleifen), 3.. Verstehen Sie die Definition und Verwendung von Funktionen, 4. Beginnen Sie schnell mit der Python -Programmierung durch einfache Beispiele und Code -Snippets.
 Navicat -Methode zum Anzeigen von MongoDB -Datenbankkennwort
Apr 08, 2025 pm 09:39 PM
Navicat -Methode zum Anzeigen von MongoDB -Datenbankkennwort
Apr 08, 2025 pm 09:39 PM
Es ist unmöglich, das MongoDB -Passwort direkt über Navicat anzuzeigen, da es als Hash -Werte gespeichert ist. So rufen Sie verlorene Passwörter ab: 1. Passwörter zurücksetzen; 2. Überprüfen Sie die Konfigurationsdateien (können Hash -Werte enthalten). 3. Überprüfen Sie Codes (May Hardcode -Passwörter).
 Wie man AWS -Kleber mit Amazon Athena verwendet
Apr 09, 2025 pm 03:09 PM
Wie man AWS -Kleber mit Amazon Athena verwendet
Apr 09, 2025 pm 03:09 PM
Als Datenprofi müssen Sie große Datenmengen aus verschiedenen Quellen verarbeiten. Dies kann Herausforderungen für das Datenmanagement und die Analyse darstellen. Glücklicherweise können zwei AWS -Dienste helfen: AWS -Kleber und Amazon Athena.
 Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Die MySQL-Datenbankleistung Optimierungshandbuch In ressourcenintensiven Anwendungen spielt die MySQL-Datenbank eine entscheidende Rolle und ist für die Verwaltung massiver Transaktionen verantwortlich. Mit der Erweiterung der Anwendung werden jedoch die Datenbankleistung Engpässe häufig zu einer Einschränkung. In diesem Artikel werden eine Reihe effektiver Strategien zur Leistungsoptimierung von MySQL -Leistung untersucht, um sicherzustellen, dass Ihre Anwendung unter hohen Lasten effizient und reaktionsschnell bleibt. Wir werden tatsächliche Fälle kombinieren, um eingehende Schlüsseltechnologien wie Indexierung, Abfrageoptimierung, Datenbankdesign und Caching zu erklären. 1. Das Design der Datenbankarchitektur und die optimierte Datenbankarchitektur sind der Eckpfeiler der MySQL -Leistungsoptimierung. Hier sind einige Kernprinzipien: Die Auswahl des richtigen Datentyps und die Auswahl des kleinsten Datentyps, der den Anforderungen entspricht, kann nicht nur Speicherplatz speichern, sondern auch die Datenverarbeitungsgeschwindigkeit verbessern.
 So starten Sie den Server mit Redis
Apr 10, 2025 pm 08:12 PM
So starten Sie den Server mit Redis
Apr 10, 2025 pm 08:12 PM
Zu den Schritten zum Starten eines Redis -Servers gehören: Installieren von Redis gemäß dem Betriebssystem. Starten Sie den Redis-Dienst über Redis-Server (Linux/macOS) oder redis-server.exe (Windows). Verwenden Sie den Befehl redis-cli ping (linux/macOS) oder redis-cli.exe ping (Windows), um den Dienststatus zu überprüfen. Verwenden Sie einen Redis-Client wie Redis-Cli, Python oder Node.js, um auf den Server zuzugreifen.
 So lesen Sie Redis -Warteschlange
Apr 10, 2025 pm 10:12 PM
So lesen Sie Redis -Warteschlange
Apr 10, 2025 pm 10:12 PM
Um eine Warteschlange aus Redis zu lesen, müssen Sie den Warteschlangenname erhalten, die Elemente mit dem Befehl LPOP lesen und die leere Warteschlange verarbeiten. Die spezifischen Schritte sind wie folgt: Holen Sie sich den Warteschlangenname: Nennen Sie ihn mit dem Präfix von "Warteschlange:" wie "Warteschlangen: My-Queue". Verwenden Sie den Befehl LPOP: Wischen Sie das Element aus dem Kopf der Warteschlange aus und geben Sie seinen Wert zurück, z. B. die LPOP-Warteschlange: my-queue. Verarbeitung leerer Warteschlangen: Wenn die Warteschlange leer ist, gibt LPOP NIL zurück, und Sie können überprüfen, ob die Warteschlange existiert, bevor Sie das Element lesen.



