Chicken Swarm Optimization, abgekürzt als CSO (Chicken Swarm Optimization), hat zwar einen Hintergrund in der sogenannten Bionik, ist aber im Wesentlichen eine Variante des Partikelschwarmalgorithmus.
Einfach ausgedrückt ist ein Partikelschwarm eine Gruppe von Partikeln, und jedes Partikel wird vom besten Partikel angezogen. Sie sind völlig gleich bis auf Position und Geschwindigkeit voneinander abhängen.
Natürlich hat auch der Partikelschwarm-Algorithmus selbst einen bionischen Hintergrund. Es heißt, er sei von einem Vogelschwarm auf der Suche nach Nahrung inspiriert worden. Dabei handelt es sich natürlich nicht um etwas anderes, als um eine Gruppe gleicher Partikel in eine Gruppe gleichberechtigter Vögel.
Der Hühnerherden-Algorithmus fügt diesen Partikeln bzw. diesen Vögeln unterschiedliche Identitätsmerkmale hinzu, sodass sie nicht mehr einander gleichwertig sind.
In der Hühnerherde gibt es mindestens drei Klassen, nämlich Hähne, Hühner und Küken. Jedes Huhn hat seine eigene Position und Geschwindigkeit. Der Unterschied besteht jedoch darin, dass der
Hahn im Prinzip nach Belieben umherlaufen kann. Aber manchmal kommt ihm die Idee, nach Futter zu greifen gleichbedeutend mit der zufälligen Auswahl eines anderen Hahns. Sein Standort hat Auswirkungen.
Die Henne ist am meisten betroffen. Einerseits muss sie die Führung des Hahns akzeptieren, andererseits muss sie mit anderen Hühnern um Futter konkurrieren.
Die Küken sind am meisten sorglos, folge einfach der Henne.
Wenn sich die Positionsbeziehung ändert, können Hühner und Küken nach und nach den ursprünglichen Anführer vergessen, was bedeutet, dass sich die Populationsbeziehung ändern kann.
Zunächst müssen Sie eine Hühnerklasse implementieren, nämlich Standort und Kategorie.
import numpy as np
from random import gauss, random
randint = np.random.randint
uniRand = np.random.uniform
class Chicken:
def __init__(self, N, xRange, order=0, kind=0):
# 生成(N)维参数
self.x = uniRand(*xRange, (N,))
self.best = np.inf
self.xBest = np.zeros((N,))
self.kind = kind # 鸡的类别
self.order = order # 鸡的编号
# 设置自己的首领公鸡
def setCock(self, i):
self.cock = i
# 设置自己的监护母鸡
def setHen(self, i):
self.hen = iArt ist in drei Kategorien unterteilt, nämlich Hahn, Henne und Küken. Unter ihnen hat jede Henne ihren eigenen Alpha-Hahn und jedes Küken seine eigene Schutzhenne.
Ordnung ist die Anzahl dieses Huhns in der Hühnerherde, die sich hauptsächlich in der Hühnerherde widerspiegelt.
Es gibt einen großen Unterschied zwischen einem Hühnerschwarm und einem Partikelschwarm. Letzterer hat letzten Endes nur einen Schwarm, aber in einem Hühnerschwarm hat jeder Hahn seine eigenen Hühner und Küken, was einer kleinen Gruppe gleichkommt . Da die Beziehung zwischen Hühnern jedoch nicht von den Hühnern selbst abhängt, muss sie in der Hühnerherde implementiert werden. Der Hahn und der Hüter der Hühner, Hühner, werden alle zufällig generiert.
Aktualisierung der Hühnerherde
Denken Sie daran, dass die aktuelle Nummer des Hahns i ist und die Nummer des zufällig ausgewählten Hahns j ist, j≠i, dann ist die Aktualisierungsmethode für die Position des i-ten Hahns
x
i(t+1) =xi(t)⋅(1+r)wobei r eine durch Normalverteilung generierte Zufallszahl ist, die ausgedrückt werden kann als 1∼N(0,σ
2), wobei σ 2
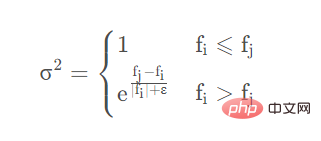ist, wobei f im Allgemeinen als Fitnessfaktor bezeichnet wird, der dem Wert entspricht, der durch das Einfügen eines bestimmten Huhns in die zu durchsuchende Funktion erhalten wird. Um beispielsweise nach dem Mindestwert von y=
zu suchen, ist f=1,52=2,25, wenn die aktuelle Position des Huhns 1,5 ist. ε ist eine kleine Größe, die Fehler bei der Division durch Null verhindert. Aber es ist zu beachten, dass alle x oben keinen Skalar darstellen, sondern ein Array.
Die Python-Implementierung ist
randint = np.random.randint
class Swarm:
# cNum 鸡数，是三个元素的列表，分别是公鸡、母鸡和小鸡数
# N参数维度
def __init__(self, cNum, N, xRange):
self.initCs(cNum, N, xRange)
self.bestCS = deepcopy(self.cs) #最佳鸡群
self.best = np.inf #全局最优值
self.xBest = np.zeros((N,)) #全局最优参数
self.N = N
def initCs(self, cNum, N, xRange, vRange):
self.cs = []
self.cNum = cNum
self.cocks = np.arange(cNum[0]) # 公鸡编号
self.hens = np.arange(cNum[0], cNum[0]+cNum[1]) #母鸡编号
self.chicks = np.arange(cNum[0]+cNum[1], np.sum(cNum)) #小鸡编号
kinds = np.repeat([0,1,2], cNum)
for i in range(sum(cNum)):
self.cs.append(Chicken(N,xRange, vRange, i, kinds[i]))
if kinds[i] > 0:
cock = randint(0, cNum[0])
self.cs[i].setCock(cock)
if kinds[i] > 1:
hen = randint(cNum[0], cNum[0]+cNum[1])
self.cs[i].setHen(hen)Angenommen, die aktuelle Hühnernummer ist i. Diese Henne muss nicht nur dem Leithahn folgen, sondern auch mit anderen Hühnern um Futter konkurrieren.
x
i(t+1)=xi(t)+k1r1(xc−xi)+k2r2( xj− k1, k2 sind Koeffizienten und ihre Aktualisierungslogik ist die gleiche wie die von Hahn. Wenn f
igrößer ist, wird es als ausgedrückt. Der Code wird als
# 写在Swarm类中
def cockStep(self):
for i in self.cocks:
# 第j只公鸡
j = np.random.randint(self.cNum[0])
if j==i:
j = (j+1) % self.cNum[0]
# 第i只公鸡
ci = self.cs[i]
# 第j只公鸡
cj = self.cs[self.cocks[j]]
sigma = 1 if cj.best > ci.best else np.exp(
(cj.best-ci.best)/(np.abs(ci.best)+1e-15))
ci.x *= 1 + gauss(0, sigma)
x
(t+1)=x
i(t)+r( xh( t)− Das Leben ist höher als das Leben, aber im Hühnerherdenalgorithmus wird tatsächlich die Stärke betont. Wenn das Huhn Glück hat und bessere Optimierungsergebnisse als der Hahn erzielt, entwickelt sich das Huhn zu einem Hahn.
Mit anderen Worten, von Zeit zu Zeit werden die Identitäten der Hühner in der Herde neu geordnet. Derjenige mit dem besten Optimierungseffekt ist der Leithahn, der schlechtere ist der Wächter, und der schlechteste kann nur sein Sei das Küken.
def henStep(self):
nGuarder = self.cNum[0] + self.cNum[1] - 2
for i in self.hens:
guarders = list(self.cocks) + list(self.hens)
c = self.cs[i].cock #首领公鸡
guarders.remove(i)
guarders.remove(c)
# 随机生成另一只监护鸡
j = guarders[np.random.randint(nGuarder)]
ci = self.cs[i]
cj = self.cs[j]
cc = self.cs[c]
k1, k2 = random(), random()
if cc.best > ci.best:
k1 *= np.exp((ci.best-cc.best)/(np.abs(ci.best)+1e-15))
if cj.best < ci.best:
k2 *= np.exp(cj.best-ci.best)
ci.x += k1*(cc.x-ci.x)+k2*(cj.x-ci.x)OptimierungsiterationAn diesem Punkt wurde das Framework des Clusteralgorithmus erfolgreich erstellt. Als nächstes wird der kritischste Teil, die Optimierung, implementiert. 其基本逻辑是，输入一个待优化func，通过将每只鸡的位置x带入到这个函数中，得到一个判定值，最后通过这个判定值，来不断更新鸡群。 除了这个函数之外，还需要输入一些其他参数，比如整个鸡群算法的迭代次数，以及鸡群更新的频次等等 其中，printBest可以将当前最佳结果打印出来，其形式为 算法完成之后，当然要找个函数测试一下，测试函数为 测试结果如下 已经迭代4次，最佳优化结果为-5.793762423022024，参数为： Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Hühnerherden-Algorithmus in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!# func为待优化函数
# N为迭代次数
# T为鸡群更新周期
def optimize(self, func, N, T, msgT):
for n in range(N):
# 计算优化参数
for c in self.cs:
c.best = func(c.x)
# 分别更新公鸡、母鸡和小鸡
self.cockStep()
self.henStep()
self.chickStep()
if (n+1)%T == 0:
self.update() #每T次更新一次种群
self.printBest(n)
self.printBest(n)def printBest(self,n):
fitness = [c.best for c in self.cs]
best = np.min(fitness)
ind = np.where(fitness==best)[0]
msg = f"已经迭代{n}次，最佳优化结果为{np.min(fitness)}，参数为：\n"
msg += ", ".join([f"{x:.6f}" for x in self.cs[ind].x])
print(msg)测试
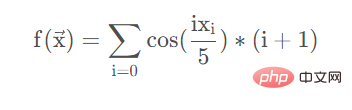
def test(xs):
_sum = 0.0
for i in range(len(xs)):
_sum = _sum + np.cos((xs[i]*i)/5)*(i+1)
return _sum
if __name__ == "__main__":
cNum = [15,20,100]
s = Swarm(cNum, 5, (-5,5))
s.optimize(test, 20, 5)
-6.599526, 3.117137, 5.959538, 7.225785, 5.204990
已经迭代9次，最佳优化结果为-10.61594651972434，参数为：
-7.003724, -5.589730, 0.981409, 12.920325, -19.006112
已经迭代14次，最佳优化结果为-9.143596747975293，参数为：
5.388234, -3.714421, -5.254391, -5.216215, -6.079223
已经迭代19次，最佳优化结果为-11.097888385616995，参数为：
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
已经迭代19次，最佳优化结果为-11.097888385616995，参数为：
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
