Integriertes neuronales Netzwerk mit mehreren Graphen

1. GNN aus einer einheitlichen Perspektive

1. Bestehendes GNN-Verbreitungsparadigma# 🎜🎜#

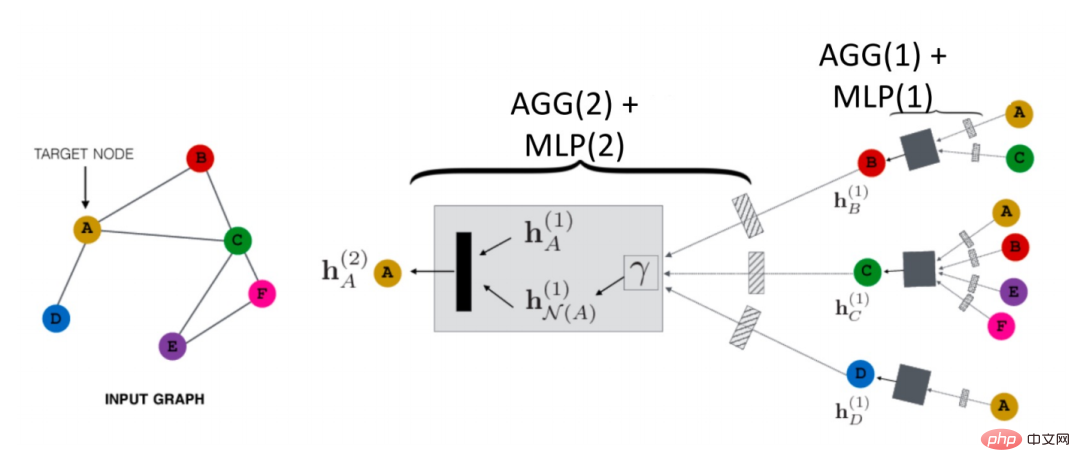
Wie breitet sich GNN im Luftraum aus? Wie in der folgenden Abbildung gezeigt, nehmen wir Knoten A als Beispiel: #🎜🎜 #Zunächst aggregiert es die Informationen seines Nachbarknotens N (A) zu einem

h

# 🎜🎜#

N(A)

(1), dann füge A hinzu zur vorherigen Darstellung von Schichten hN(A)#🎜 🎜#(1 ) wird kombiniert, und dann wird durch eine Transformationsfunktion (d. h. Trans(·) in der Formel) die Darstellung der nächsten Ebene von A erhalten # 🎜🎜# h N(A)₍₂₎^{. Dies ist das grundlegendste GCN-Verbreitungsparadigma.} Darüber hinaus gibt es noch eine weitere Lösung: Entkoppelter Ausbreitungsprozess: 🎜🎜#Was ist der Unterschied zwischen diesen beiden Methoden?

Im entkoppelten Ausbreitungsparadigma wird zunächst ein Feature-Extraktor, also die Transformationsfunktion, zum Extrahieren der anfänglichen Features verwendet, und dann werden die extrahierten Features zur Aggregation in die Aggregationsfunktion eingefügt siehe Auf diese Weise werden Merkmalsextraktion und Aggregation getrennt, dh eine Entkopplung erreicht. Der Vorteil davon ist: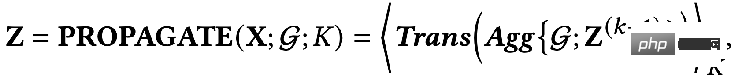

Sie können die bisherige Transformationsfunktion frei gestalten und ein beliebiges Modell verwenden.

Während der Aggregation können viele Ebenen hinzugefügt werden, um Verbindungsinformationen über größere Entfernungen zu erhalten, aber wir werden nicht mit einer Überparametrisierung konfrontiert, weil dort ein Risiko besteht Es gibt keine Parameter in der Aggregatfunktion, die optimiert werden müssen.

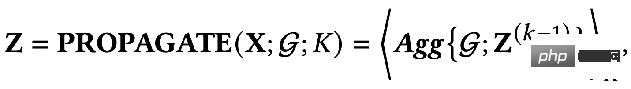
Die oben genannten sind die beiden Hauptparadigmen, und die Einbettungsausgabe des Knotens kann die letzte Ebene des verwenden Netzwerk oder Die Residuen aus der Zwischenschicht können verwendet werden.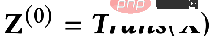

Anhand der obigen Überprüfung können wir erkennen, dass es in GNN zwei grundlegende Informationsquellen gibt: # 🎜🎜#

• Die topologische Struktur des Netzwerks: Im Allgemeinen können die Sortimentsinformationsattribute der Diagrammstruktur erfasst werden.
• Eigenschaften von Knoten: Umfasst im Allgemeinen niederfrequente und hochfrequente Signale von Knoten.

2. Ein einheitliches Optimierungsframework#🎜🎜 # Basierend auf dem Ausbreitungsmechanismus von GNN können wir feststellen, dass bestehende GNNs zwei gemeinsame Ziele haben:

• Kodieren Sie nützliche Informationen aus den Eigenschaften von Knoten.
• Nutzen Sie die Glättungsfunktionen der Topologie.

Können wir also eine mathematische Sprache verwenden, um diese beiden Ziele zu beschreiben? Jemand hat das folgende einheitliche GNN-Optimierungsframework vorgeschlagen, das durch die Formel ausgedrückt wird:

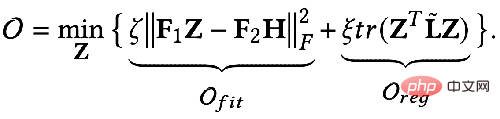
Das erste Element im Optimierungsziel:

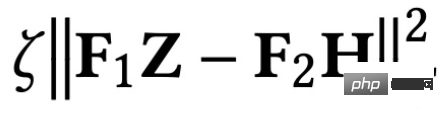
ist der Merkmalsanpassungsbegriff, den The Ziel ist es, die erlernte Knotendarstellung Z so nah wie möglich an das ursprüngliche Merkmal H und F zu bringen. Wenn der Faltungskern die Identitätsmatrix I ist, entspricht er einem Allpassfilter. Wenn der Faltungskern eine 0-Matrix ist, ist er ein Tiefpassfilter, und wenn der Faltungskern die Laplace-Matrix L ist, ist er ein Tiefpassfilter ein Hochpassfilter. Der zweite Term des Optimierungsziels ist formal die Spur einer Matrix, und seine Funktion ist der reguläre Term im Diagramm. Welche Beziehung besteht zwischen der Spur und dem regulären Term? Tatsächlich wird der zweite Term in die folgende Form erweitert: Seine Bedeutung besteht darin, den Grad der Merkmalsdifferenz zwischen zwei benachbarten Knoten im Diagramm zu erfassen, der die Glätte von darstellt eine Grafik. Dieses Ziel zu minimieren ist gleichbedeutend damit, mich und meinen Nachbarn ähnlicher zu machen. 3. Verwenden Sie ein einheitliches Optimierungsframework, um das vorhandene GNN zu verstehen. GNN optimiert dieses Ziel hauptsächlich in verschiedenen Situationen:

Wenn die Parameter: Wenn

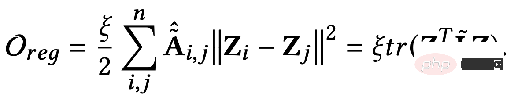
Das Optimierungsziel lautet:

Die partielle Ableitung wird erhalten:

Lassen Sie uns die erzielten Ergebnisse auf den Punkt bringen weiter erweitert werden, um Folgendes zu erhalten:

Dies bedeutet, dass alle Knotendarstellungen der K-ten Schicht dem Ausbreitungsprozess der Knotendarstellungen der K-1-ten Schicht auf der Adjazenzmatrix und danach entsprechen Nach der Ableitung bis zum Ende werden Sie feststellen, dass dies dem anfänglichen Merkmal X entspricht, das nach Abschluss der Merkmalstransformation W* K-mal auf der Adjazenzmatrix propagiert wird. Tatsächlich ist dies das Modell von GCN oder SGC, bei dem die nichtlineare Schicht entfernt wurde.

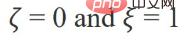
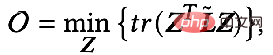
Wenn die Parameter F

1

=F

2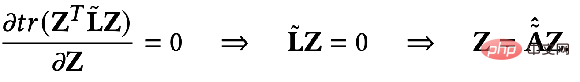=I, ζ=1, ξ=1/α-1, α∈(0,q], und wählen Sie einen Allpassfilter zur Optimierung aus das Ziel Es wird:

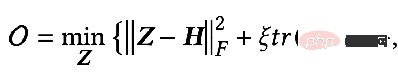
Zu diesem Zeitpunkt ermitteln wir auch die partielle Ableitung von Z und setzen die partielle Ableitung auf 0, um die geschlossene Lösung des Optimierungsziels zu erhalten:

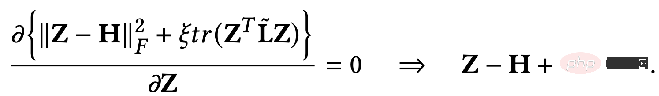
Transformieren Sie das Ergebnis leicht. Sie können die folgende Formel erhalten:

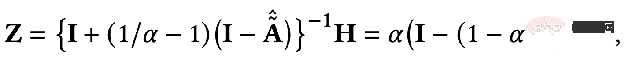
Wir können feststellen, dass die obige Formel den Prozess der Ausbreitung von Knotenmerkmalen auf dem personalisierten PageRank darstellt, dem PPNP-Modell.

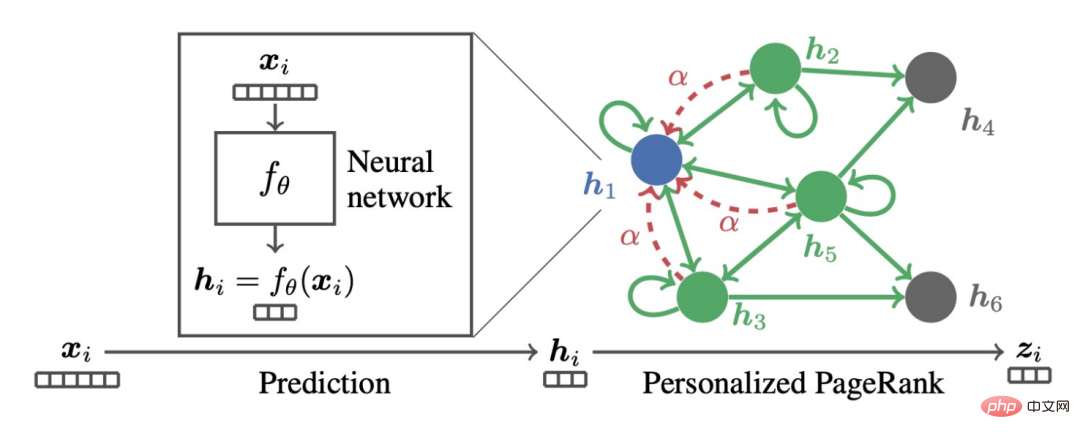
ist auch ein solches Modell. Wenn Sie es mithilfe des Gradientenabstiegs finden und die Schrittgröße auf b setzen, ist der Iterationsterm die partielle Ableitung der Zielfunktion zum Zeitpunkt k-1 mit Respekt vor Z.

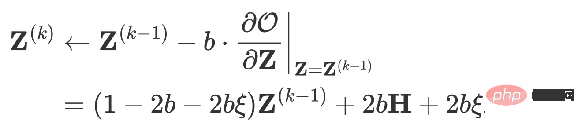
Wenn Sie Folgendes erhalten:

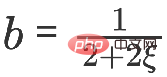
Dies ist das APPNP-Modell. Der Hintergrund für die Entstehung des APPNP-Modells besteht darin, dass die Umkehroperation der Matrix im PPNP-Modell zu kompliziert ist und APPNP zur Lösung eine iterative Näherung verwendet. Es ist auch verständlich, dass APPNP zu PPNP konvergieren kann, da beide aus demselben Framework stammen. 4. Neues GNN-Framework

und entwerfen Sie ein entsprechendes Diagramm Begriff

O

reg

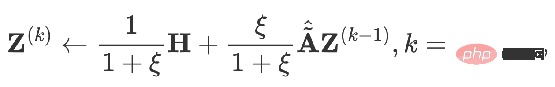
, plus ein neuer Lösungsprozess, kann ein neues GNN-Modell erhalten.

① Beispiel 1: Von der Allpassfilterung zur Tiefpassfilterung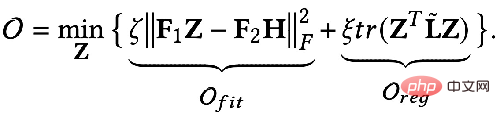

Wie bereits erwähnt, der Faltungskern unter dem Allpassfilter

F

1= F2=_I Wenn der Faltungskern die Laplace-Matrix L ist, handelt es sich um einen Hochpassfilter. Wenn das durch Gewichtung dieser beiden Situationen erhaltene GNN Tiefpassinformationen codieren kann:

kann die genaue Lösung erhalten:

# 🎜🎜#

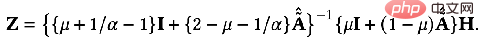
Ähnlich können wir es iterativ lösen: 5, Elastic GNN

#🎜 🎜#

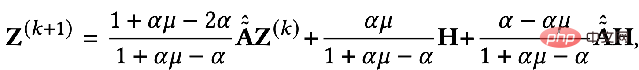Die im vorherigen einheitlichen Framework erwähnten regulären Terme entsprechen L2 regulär, was der Berechnung der Differenzinformationen zwischen zwei beliebigen Punkten im Diagramm entspricht. Einige Forscher sind der Meinung, dass die L2-Regularisierung zu global ist und dazu führt, dass die Glätte des gesamten Diagramms tendenziell gleich ist, was nicht ganz mit der Realität übereinstimmt. Daher wurde vorgeschlagen, einen regulären L1-Term hinzuzufügen. Der reguläre L1-Term würde relativ große Änderungen im Diagramm benachteiligen. #? :

Kurz gesagt, das Obige Dieses einheitliche Framework sagt uns:

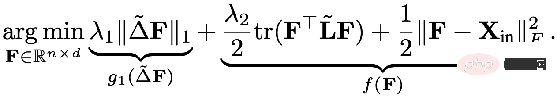
Wir können eine eher makroökonomische Perspektive verwenden, um GNN# 🎜 zu verstehen 🎜#

Wir können von diesem einheitlichen Framework ausgehen, um ein neues GNN zu entwerfen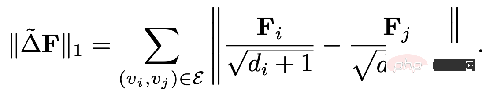

#🎜🎜 #

Dieses einheitliche Framework kann jedoch nur an homogene Graphstrukturen angepasst werden. Als nächstes werfen wir einen Blick auf die häufigere Multi-Relationship-Graphstruktur.

2. Relationales GNN-Modell

• 1, RGCN#🎜 🎜#
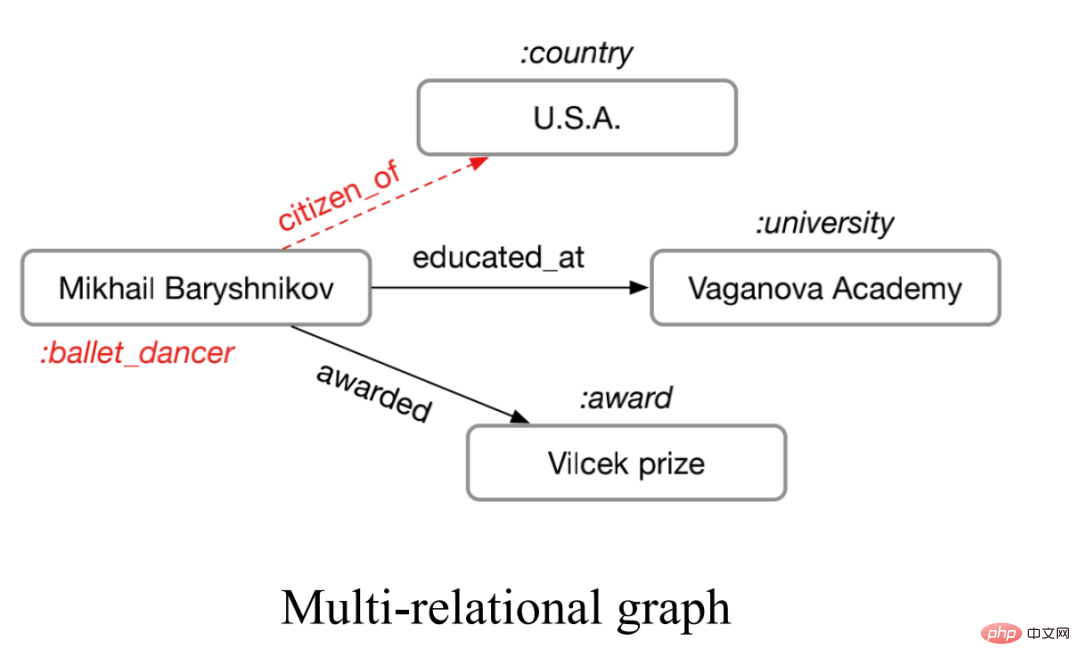
• Der sogenannte Multi-Relationship-Graph bezieht sich auf einen Graphen mit mehr als einem Kantentyp, wie in der folgenden Abbildung dargestellt.

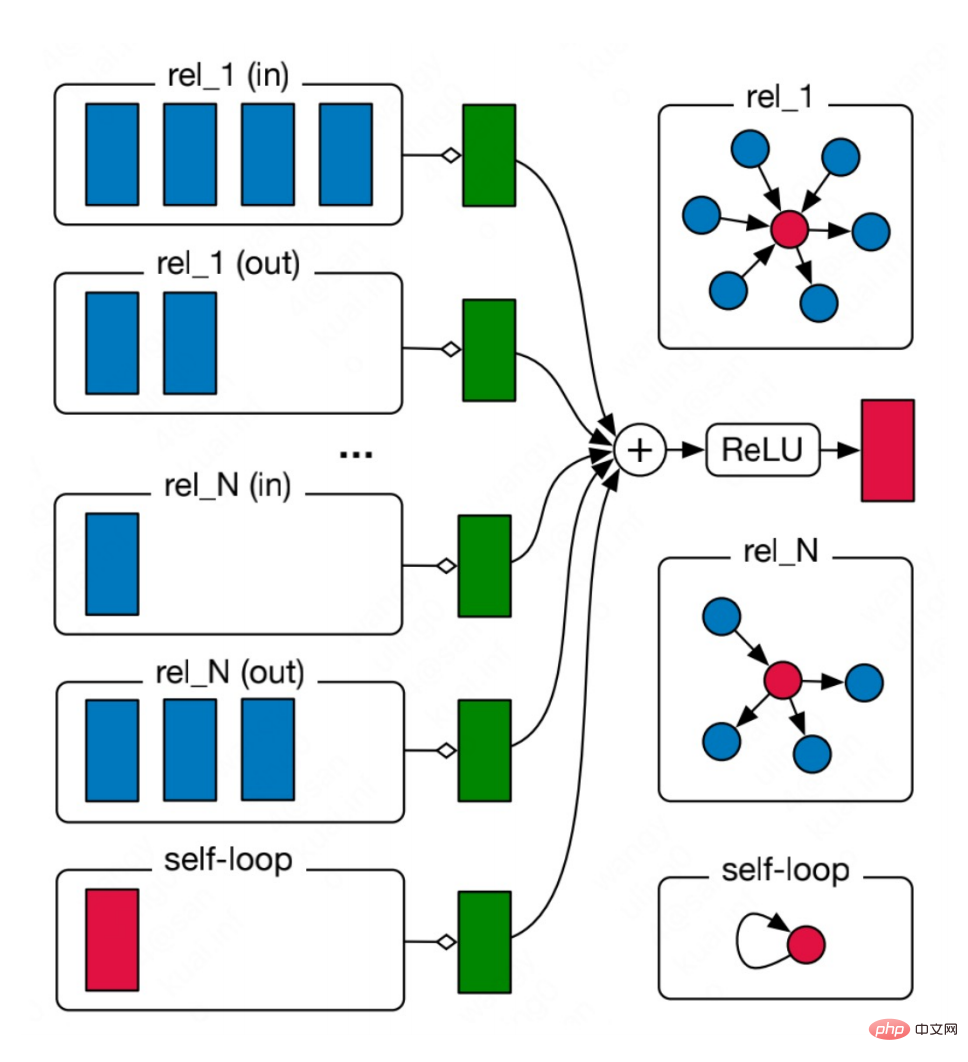
Diese Art von Multibeziehung Das Diagramm ist in der realen Welt sehr weit verbreitet, beispielsweise die vielfältigen Arten molekularer Bindungen in chemischen Molekülen und die unterschiedlichen Beziehungen zwischen Menschen in Diagrammen sozialer Beziehungen. Für solche Diagramme können wir neuronale Netzwerke mit relationalen Diagrammen zur Modellierung verwenden. Die Hauptidee besteht darin, Diagramme mit N Beziehungen einzeln zu aggregieren, um N Aggregationsergebnisse zu erhalten, und dann die N Ergebnisse zu aggregieren.

Die Formel lautet: # 🎜 🎜#

Sie können sehen, dass die Aggregation geteilt ist in zwei Schritte Um fortzufahren, wählen Sie zunächst eine Beziehung r aus allen Beziehungen R aus und suchen Sie dann alle Knoten, die diese Beziehung enthalten. 🎜🎜#r

wird aggregiert, wobei

W

r

ist das Gewicht, mit dem verschiedene Beziehungen gewichtet werden. Daher können Sie sehen, dass mit zunehmender Anzahl von Beziehungen im Diagramm auch die Gewichtsmatrix Wr

zunimmt, was ebenfalls der Fall ist führt zu Das Problem der Überparametrisierung (Überparametrisierung). Darüber hinaus kann die Aufteilung des topologischen Beziehungsdiagramms nach Beziehungen auch zu einer Überglättung führen.

2. CompGCN Selbstschleifenbeziehungen in drei Richtungen:

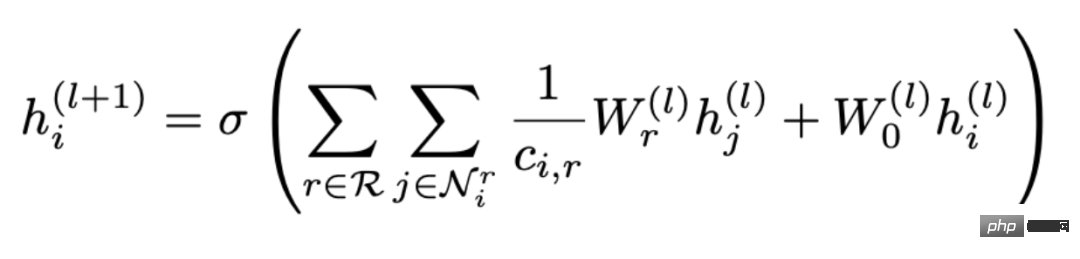
Die Einbettung der Beziehung wird ebenfalls bei jeder Iteration aktualisiert.

Aber dieses heuristische Design und ein solcher parametrischer Encoder können auch zu einer übermäßigen Parametrisierung führen. Basierend auf den obigen Überlegungen erhalten wir dann den Ausgangspunkt unserer Arbeit: Können wir aus Sicht der Optimierungsziele ein zuverlässigeres GNN entwerfen und gleichzeitig die Probleme bestehender GNNs lösen? ?? 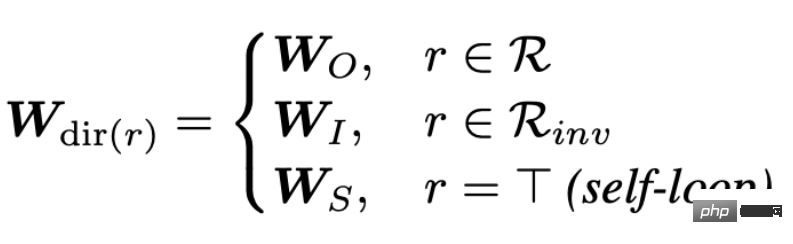So entwerfen Sie einen geeigneten integrierten Optimierungsalgorithmus?

Dieser Optimierungsalgorithmus muss zwei Anforderungen erfüllen:

In der Lage sein, mehrere Beziehungen gleichzeitig im Diagramm zu erfassen

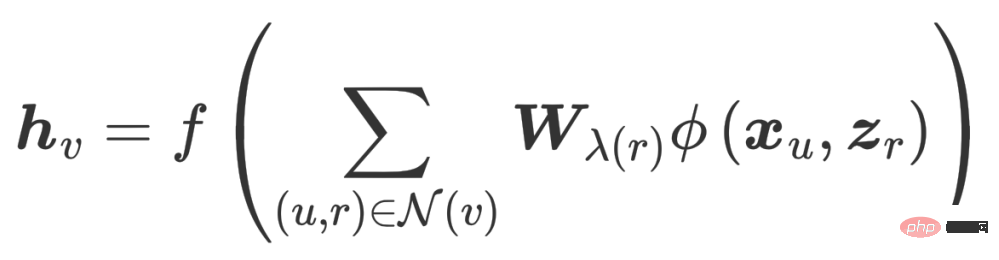
In der Lage sein, die Bedeutung verschiedener Beziehungen im Diagramm zu modellieren

Wir Der im Multi-Beziehungsdiagramm vorgeschlagene reguläre Begriff des integrierten Multi-Beziehungsdiagramms lautet wie folgt:

Dieser reguläre Begriff dient auch dazu, die Glättungsfähigkeit des Diagrammsignals zu erfassen. Diese Adjazenzmatrix basiert jedoch auf der Beziehung r Erfasst, und die Parameter unterliegen Normalisierungsbeschränkungen
• μ
• r

dienen dazu, die Bedeutung von a zu modellieren bestimmte Beziehung. Der zweite Term ist die zweite Normalform-Regularisierung des Koeffizientenvektors, die den Koeffizientenvektor gleichmäßiger machen soll.

• Um das Problem der Überglättung zu lösen, haben wir einen passenden Begriff hinzugefügt, um sicherzustellen, dass die ursprünglichen Feature-Informationen nicht verloren gehen. Die Summe aus dem Anpassungsterm und dem regulären Term ist:

Verglichen mit dem im vorherigen Kapitel erwähnten einheitlichen Framework umfasst die hier entworfene Zielfunktion zwei Knotenkorrektur-Z- und Beziehungsmatrixparameter μ Variable. Daher ist es auch eine Herausforderung, einen Mechanismus zur Nachrichtenverbreitung abzuleiten, der auf einem solchen Optimierungsziel basiert.

2. Ableitung des Message-Passing-Mechanismus

Hier übernehmen wir eine iterative Optimierungsstrategie: #🎜🎜 #

• Fixieren Sie zuerst die Knotendarstellung Z und optimieren Sie dann den Parameter μ#🎜🎜 #
• Optimieren Sie gemäß dem Ergebnis μ der vorherigen Iteration die Knotendarstellung Z

#🎜🎜 # Wenn der feste Knoten Z darstellt, degeneriert das gesamte Optimierungsziel in eine Zielfunktion, die sich nur auf μ bezieht, aber dies ist eine eingeschränkte Zielfunktion: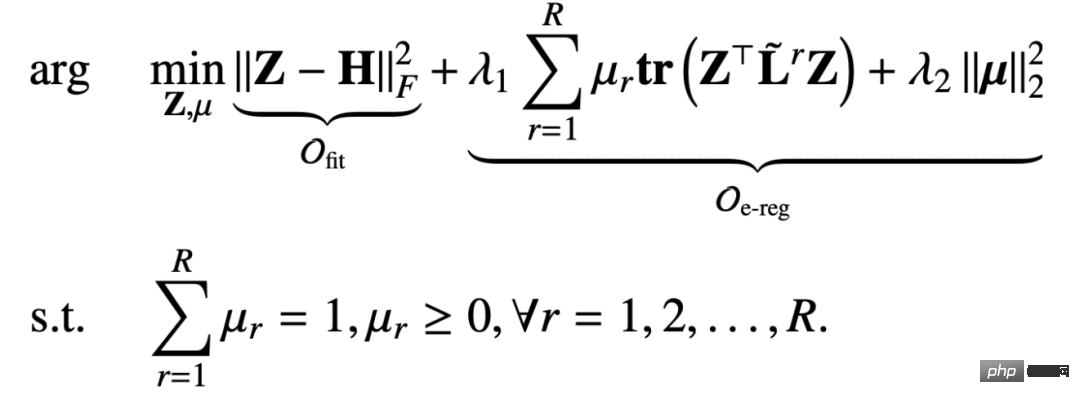

#🎜 🎜#

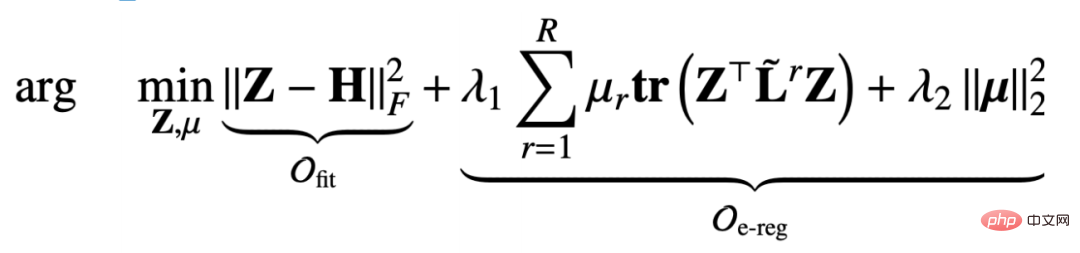Dies ist tatsächlich eine konvexe Funktion von μ auf einer Simplex-Einschränkung (Einschränkung in einem Standard-Simplex). Spiegel-Entropie-Abstiegsalgorithmus zur Lösung dieses Problems. Wir werden zuerst eine Konstante finden und dann den Gewichtskoeffizienten unter jeder Beziehung aktualisieren. Der gesamte Aktualisierungsprozess ähnelt dem exponentiellen Gradientenabstiegsalgorithmus.

Fester Beziehungskoeffizient μ Gehe zu Update Z, das Optimierungsziel zu diesem Zeitpunkt degeneriert in die folgende Form:

#🎜🎜 #

Auf diese Weise ermitteln wir die partielle Ableitung der Zielfunktion nach Z und setzen die partielle Ableitung gleich 0, um Folgendes zu erhalten:

# 🎜🎜#

Dann lautet die geschlossene Lösung von Z: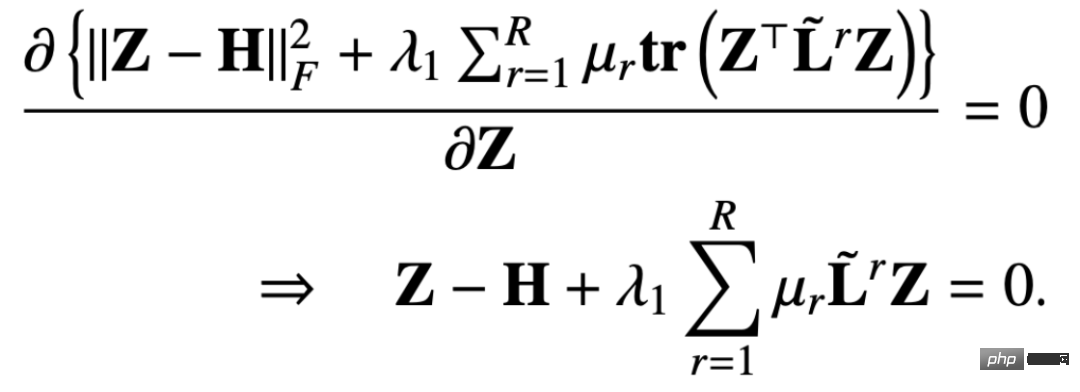

#🎜 🎜##🎜 🎜#

In ähnlicher Weise können wir Iteration verwenden, um eine ungefähre Lösung zu erhalten ausgedrückt wie folgt:

# Aus dem abgeleiteten Nachrichtenübermittlungsmechanismus können wir beweisen, dass dieses Design eine übermäßige Glättung und Überparametrisierung vermeiden kann. Nachfolgend können wir uns den Beweisprozess ansehen.

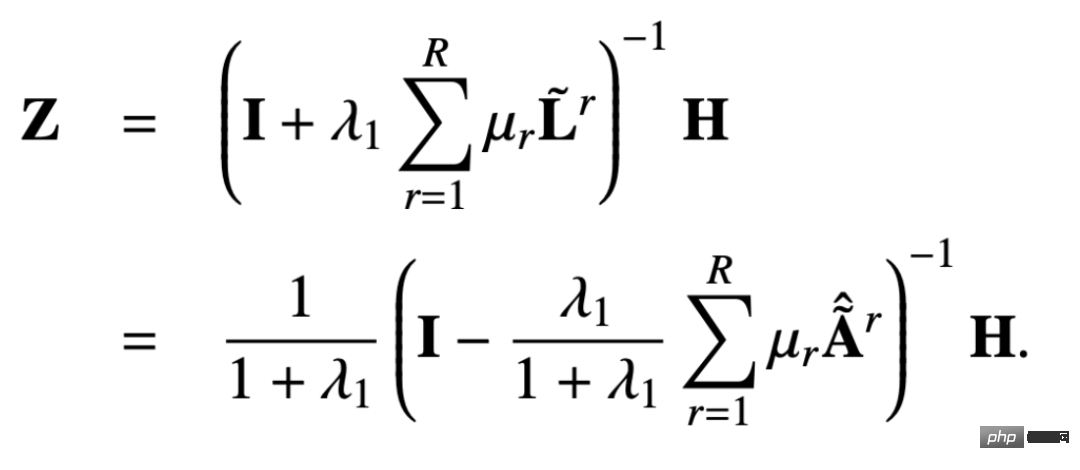
Die ursprüngliche Multi-Relationship-PageRank-Matrix ist wie folgt definiert: #🎜🎜 #

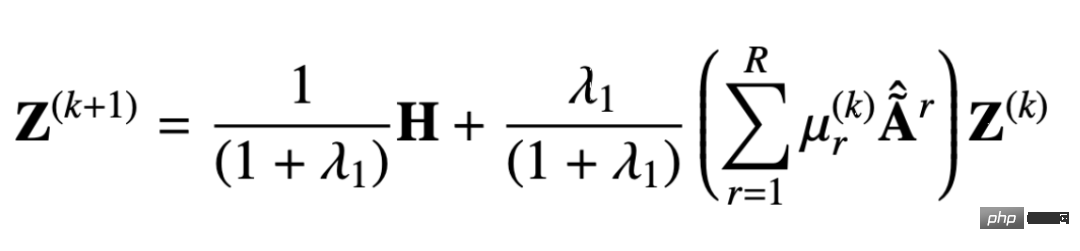
Die personalisierte Multi-Relationship-PageRank-Matrix fügt eine Wahrscheinlichkeit hinzu, dass auf dieser Basis ein eigener Knoten zurückgegeben wird : # Durch Lösen der obigen Schleifengleichung können Sie die personalisierte PageRank-Matrix mit mehreren Beziehungen erhalten:

#🎜🎜 #

Wir vermieten: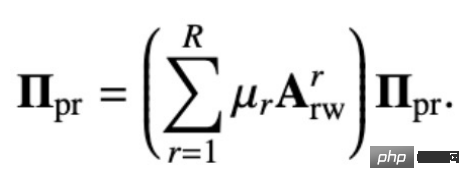

kann erhalten werden:

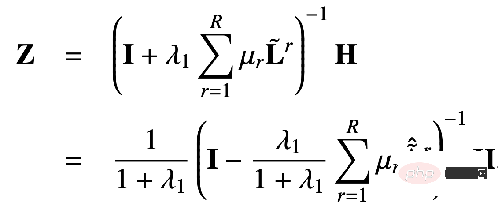
Dies ist die geschlossene Lösung, die durch unseren Lösungsvorschlag erhalten wird. Das heißt, unser Ausbreitungsmechanismus kann der Ausbreitung von Merkmal H auf der personalisierten PageRank-Matrix des Knotens entsprechen. Denn bei diesem Ausbreitungsmechanismus kann ein Knoten mit einer bestimmten Wahrscheinlichkeit zu seinem eigenen Knoten zurückkehren, was bedeutet, dass seine eigenen Informationen während des Informationsübertragungsprozesses nicht verloren gehen, wodurch das Problem der Überglättung vermieden wird.

Darüber hinaus mildert unser Modell auch das Phänomen der Überparametrisierung, denn wie Sie der Formel entnehmen können, hat unser Modell nur einen lernbaren Koeffizienten für jede Beziehung μ _r Im Vergleich zum vorherigen Encoder oder der Gewichtsmatrix w_r Im Vergleich zur Anzahl der Parameter ist die Größe unserer Parameter nahezu vernachlässigbar. Die folgende Abbildung zeigt die von uns entworfene Modellarchitektur:

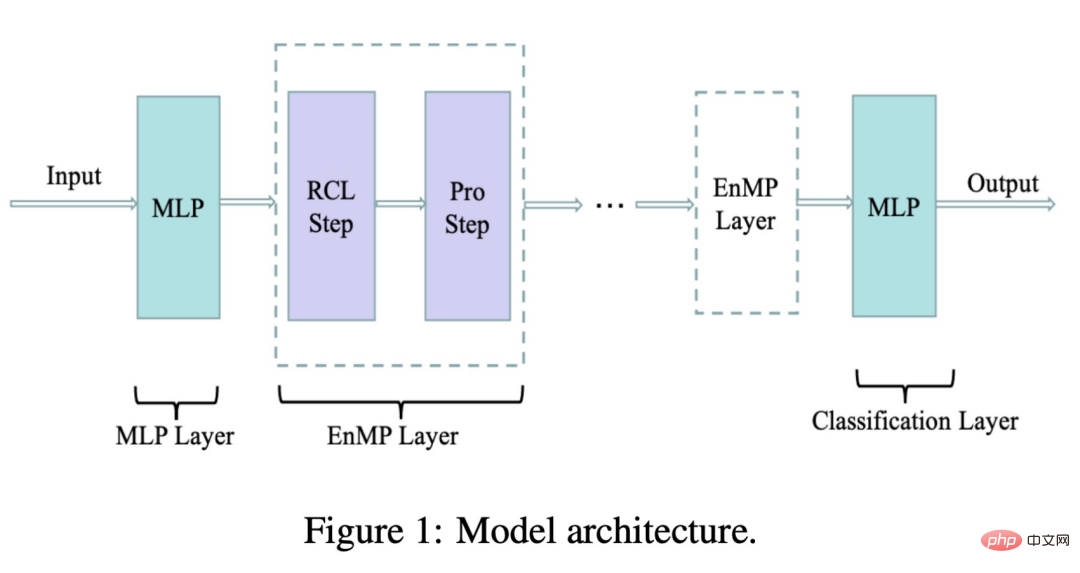
wobei RCL der Schritt des Parameterlernens und der Pro-Schritt der Schritt der Feature-Weitergabe ist. Diese beiden Schritte bilden zusammen unsere Nachrichtenschicht. Wie integrieren wir also unsere Messaging-Schicht in das DNN, ohne weitere zusätzliche Parameter einzuführen? Wir folgen auch der Idee des Entkopplungsdesigns: Verwenden Sie zunächst ein MLP, um Eingabemerkmale zu extrahieren, und durchlaufen Sie dann mehrere Ebenen der von uns entworfenen Nachrichtenübermittlungsebenen. Das Überlagern mehrerer Ebenen führt nicht zu einer übermäßigen Glättung. Das endgültige Übertragungsergebnis wird von MLP zur vollständigen Knotenklassifizierung verarbeitet und kann für nachgelagerte Aufgaben verwendet werden. Der obige Prozess wird wie folgt mit einer Formel ausgedrückt:

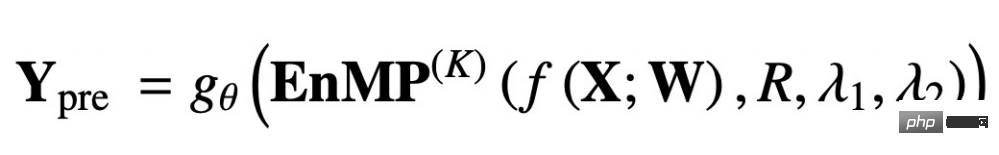
f(X;W) bedeutet, dass die Eingabemerkmale durch MLP extrahiert werden, und das folgende EnMP(K) bedeutet, dass die Extraktionsergebnisse vorliegen werden durch K-Schichten geleitet. Die Nachrichtenübermittlung g_θ stellt ein klassifiziertes MLP dar.

Bei der Backpropagation müssen wir nur die Parameter in den beiden MLPs aktualisieren, und die Parameter in unserem EnMP werden während des Vorwärtspropagierungsprozesses gelernt. Es besteht keine Notwendigkeit, EnMP-Parameter während des Rückwärtspropagierungsprozesses zu aktualisieren .

Wir können die Parameter verschiedener Mechanismen vergleichen. Wir können sehen, dass die Parameter unseres EMR-GNN hauptsächlich aus den beiden MLPs davor und danach sowie dem Beziehungskoeffizienten stammen. Wenn die Anzahl der Schichten größer als 3 ist, können wir wissen, dass die Anzahl der Parameter von EMR-GNN geringer ist als die von GCN und sogar geringer als die anderer heterogener Diagramme.

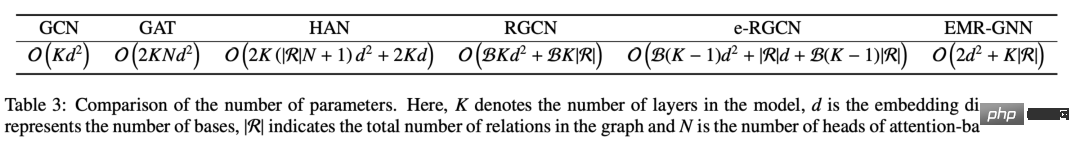
Mit einer so geringen Anzahl von Parametern kann unser EMR-GNN bei verschiedenen Knotenklassifizierungsaufgaben wie folgt immer noch das beste Niveau erreichen.

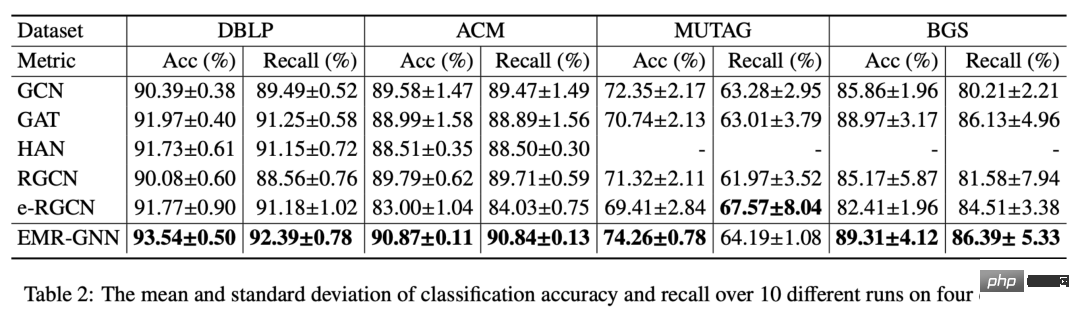
Darüber hinaus haben wir auch die Änderungen der Klassifizierungsgenauigkeit verschiedener Netzwerkstrukturen verglichen, nachdem die Anzahl der Schichten erhöht wurde. Wie in der folgenden Abbildung gezeigt, kann unser Modell immer noch eine hohe Genauigkeit beibehalten Wenn die Anzahl der Schichten auf mehr als 16 ansteigt, wird das ursprüngliche RGCN auf unzureichenden Speicher stoßen und es ist nicht möglich, weitere Schichten zu überlagern. Dies liegt an zu vielen Parametern. Die Leistung des GAT-Modells wird durch übermäßige Glättung beeinträchtigt.

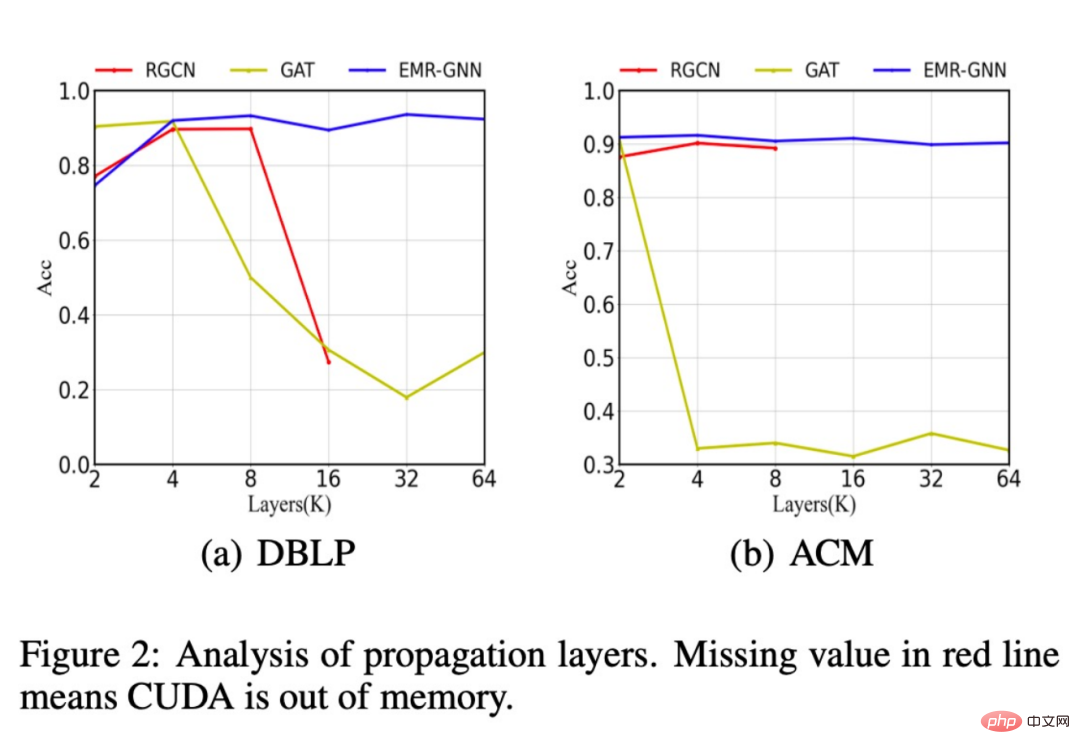
Darüber hinaus haben wir festgestellt, dass unser EMR-GNN die Klassifizierungsgenauigkeit der gesamten Stichprobe bei einer kleineren Datengröße erreichen kann, während RGCN stark abnimmt.

Wir haben auch analysiert, ob der von EMR-GNN gelernte Beziehungskoeffizient μr wirklich aussagekräftig ist. Was ist also sinnvoll? Wir möchten, dass der Beziehungskoeffizient wichtige Beziehungen stärker und unwichtigere Beziehungen weniger gewichtet. Die Ergebnisse unserer Analyse sind in der folgenden Abbildung dargestellt: Das grüne Balkendiagramm stellt den Effekt der Klassifizierung unter einer Beziehung dar. Wenn die Klassifizierungsgenauigkeit unter einer bestimmten Beziehung höher ist, werden wir dies tun Beziehung kann als wichtig angesehen werden. Die blauen Spalten stellen die von unserem EMR-GNN gelernten Beziehungskoeffizienten dar. Der Vergleich zwischen Blau und Grün zeigt, dass unser Beziehungskoeffizient die Bedeutung der Beziehung widerspiegeln kann.

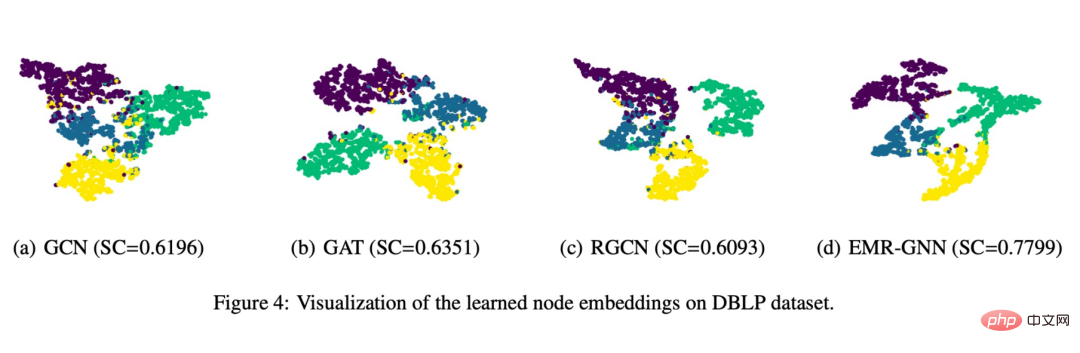
Schließlich haben wir auch eine visuelle Anzeige erstellt, wie in der folgenden Abbildung gezeigt: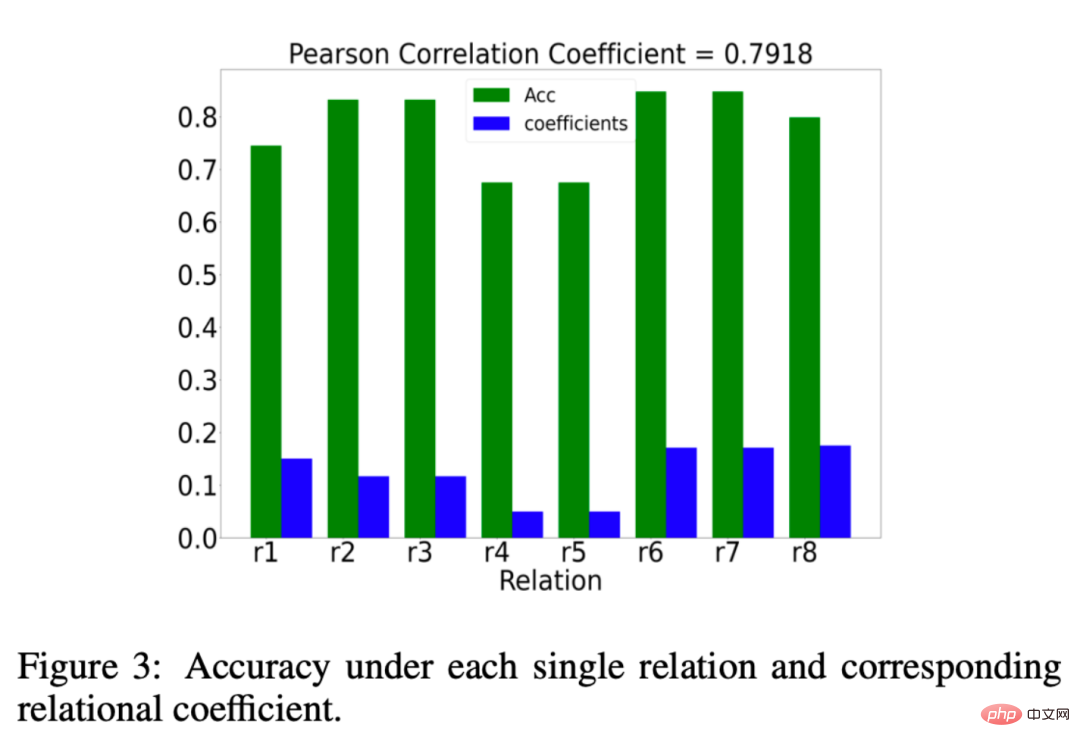

Sie können sehen, dass die von EMR-GNN trainierte Knoteneinbettung die strukturierten Informationen des tragen kann Es kann Knoten desselben Typs kohärenter machen, verschiedene Knotentypen so weit wie möglich trennen und die Segmentierungsgrenzen klarer machen als bei anderen Netzwerken.

4. Zusammenfassung

1. Wir verwenden eine einheitliche Perspektive, um GNN zu verstehen ② Dies Eine einheitliche Perspektive kann uns eine Grundlage für die Neugestaltung von GNN geben

2 Wir versuchen, ein neues Multi-Beziehungs-GNN aus der Perspektive der Zielfunktion zu entwerfen

② Basierend auf einem solchen Optimierungsframework haben wir einen Nachrichtenübermittlungsmechanismus abgeleitet

③ Dieser Nachrichtenübermittlungsmechanismus mit einer kleinen Anzahl von Parametern wird einfach mit MLP kombiniert, um EMR-GNN zu erhalten

3. Was sind die Vorteile von EMR-GNN?

① Es basiert auf einem zuverlässigen Optimierungsziel, sodass die erzielten Ergebnisse glaubwürdig sind und die zugrunde liegenden Prinzipien mathematisch erklärt werden können

② Es kann das Überglättungsproblem des bestehenden Beziehungs-GNN lösen

③ Parametrisierungsproblem gelöst

④ Leicht zu trainieren, bessere Ergebnisse können mit kleineren Parametern erzielt werden

5. Frage-und-Antwort-Sitzung

F1: Gibt es einen Unterschied zwischen dem Erlernen von Beziehungskoeffizienten und dem Aufmerksamkeitsmechanismus?

A1: Das Lernen des Beziehungskoeffizienten ist hier ein Aktualisierungsprozess, der durch das Optimierungsframework abgeleitet wird, während Aufmerksamkeit ein Prozess ist, der auf der Grundlage der Backpropagation erlernt werden muss, sodass sich die beiden hinsichtlich der Optimierung wesentlich unterscheiden.

F2: Wie ist die Anwendbarkeit des Modells auf große Datensätze?

A2: Wir haben die Komplexität des Modells im Anhang analysiert. In Bezug auf die Komplexität liegen wir auf dem gleichen Niveau wie RGCN, aber die Anzahl der Parameter wird kleiner sein als bei RGCN, sodass unser Modell besser geeignet ist umfangreicher Datensatz.

F3: Kann dieses Framework Kanteninformationen integrieren?

A3: Kann in das passende Semester oder reguläre Semester integriert werden.

F4: Wo soll ich diese mathematischen Grundlagen lernen?

A4: Ein Teil davon basiert auf früheren Arbeiten, und der andere Teil der mathematischen Theorie im Zusammenhang mit der Optimierung wird auch in einigen klassischeren Optimierungspapieren verwendet.

F5: Was ist der Unterschied zwischen Beziehungsdiagramm und heterogenem Diagramm?

A5: Der Beziehungsgraph ist ein heterogener Graph, aber wir stellen uns heterogene Graphen normalerweise als solche vor, deren Knotentypen oder Kantentypen größer als 1 sind. Im Beziehungsdiagramm sind wir besonders besorgt über die Beziehungskategorie größer als 1. Es versteht sich, dass Letzteres Ersteres einschließt.

F6: Kann es Mini-Batch-Training unterstützen?

A6: Unterstützung.

F7: Ist die zukünftige Forschungsrichtung von GNN eher auf eine strenge und interpretierbare mathematische Ableitung als auf ein heuristisches Design ausgerichtet?

A7: Wir selbst halten die streng interpretierbare mathematische Ableitung für eine zuverlässige Entwurfsmethode.

Das obige ist der detaillierte Inhalt vonIntegriertes neuronales Netzwerk mit mehreren Graphen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!