
(1) Die Identitätsmatrix
ist eine quadratische Matrix, in der die Elemente auf der Hauptdiagonale alle 1 und die übrigen Elemente 0 sind.
In NumPy können Sie die Augenfunktion verwenden, um ein solches zweidimensionales Array zu erstellen. Wir müssen nur einen Parameter angeben, um die Anzahl der 1 Elemente in der Matrix anzugeben.
Erstellen Sie beispielsweise ein Array von 3×3:
import numpy as np I2 = np.eye(3) print(I2) [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
(2) Verwenden Sie die savetxt-Funktion, um Daten in einer Datei zu speichern. Natürlich müssen wir den Dateinamen und das zu speichernde Array angeben.
np.savetxt('eye.txt', I2)#创建一个eye.txt文件,用于保存I2的数据
Das CSV-Format (Comma-Separated Value) ist normalerweise ein CSV-Format und jedes Feld in der Datei entspricht einer Spalte in einer Datenbanktabelle. Tabellenkalkulationssoftware (z. B. Microsoft Excel) kann CSV-Dateien verarbeiten.
Hinweis: Die Funktion „loadtxt“ in NumPy kann problemlos CSV-Dateien lesen, Felder automatisch segmentieren und Daten in NumPy-Arrays laden = Average()-Funktion
VWAP-Übersicht: VWAP (Volumengewichteter Durchschnittspreis) ist eine sehr wichtige wirtschaftliche Größe, die den „durchschnittlichen“ Preis von Finanzanlagen darstellt.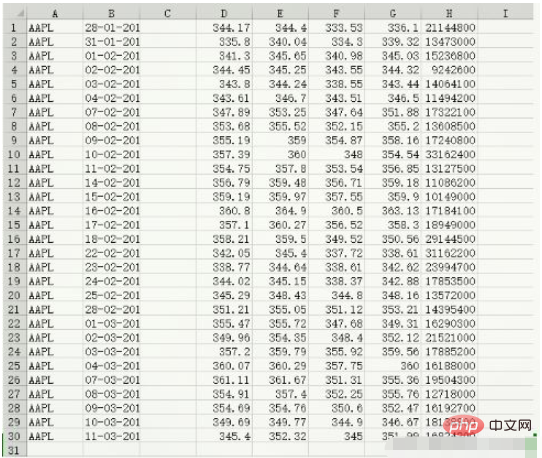 Je höher das Volumen eines bestimmten Preises, desto größer ist das Gewicht dieses Preises.
Je höher das Volumen eines bestimmten Preises, desto größer ist das Gewicht dieses Preises.
c, v = np.loadtxt('data.csv', delimiter=',', usecols=(6,7), unpack=True) # usecols的参数为一个元组,以获取第7字段至第8字段的数据 # unpack参数设置为True,意思是分拆存储不同列的数据,即分别将收盘价和成交量的数组赋值给变量c和v print(c) [336.1 339.32 345.03 344.32 343.44 346.5 351.88 355.2 358.16 354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62 342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36 355.76 352.47 346.67 351.99] print(v) [21144800. 13473000. 15236800. 9242600. 14064100. 11494200. 17322100. 13608500. 17240800. 33162400. 13127500. 11086200. 10149000. 17184100. 18949000. 29144500. 31162200. 23994700. 17853500. 13572000. 14395400. 16290300. 21521000. 17885200. 16188000. 19504300. 12718000. 16192700. 18138800. 16824200.] print(type(c)) print(type(v)) <class 'numpy.ndarray'> <class 'numpy.ndarray'>
Die Mittelwertfunktion in NumPy kann das arithmetische Mittel von Array-Elementen berechnen
vwap = np.average(c,weights=v) print('成交量加权平均价格vwap =', vwap) 成交量加权平均价格vwap = 350.5895493532009
print('c数组中元素的算数平均值为: {}'.format(np.mean(c)))
c数组中元素的算数平均值为: 351.0376666666667t = np.arange(len(c)) print('时间加权平均价格twap=', np.average(c, weights=t)) 时间加权平均价格twap= 352.4283218390804
Median: Wir können einige Schwellenwerte verwenden, um Ausreißer zu entfernen, aber es gibt tatsächlich einen besseren Weg, nämlich den Median.
h, l = np.loadtxt('data.csv', delimiter=',', usecols=(4,5), unpack=True)
print('h数据为: \n{}'.format(h))
print('-'*10)
print('l数据为: \n{}'.format(l))
h数据为:
[344.4 340.04 345.65 345.25 344.24 346.7 353.25 355.52 359. 360.
357.8 359.48 359.97 364.9 360.27 359.5 345.4 344.64 345.15 348.43
355.05 355.72 354.35 359.79 360.29 361.67 357.4 354.76 349.77 352.32]
----------
l数据为:
[333.53 334.3 340.98 343.55 338.55 343.51 347.64 352.15 354.87 348.
353.54 356.71 357.55 360.5 356.52 349.52 337.72 338.61 338.37 344.8
351.12 347.68 348.4 355.92 357.75 351.31 352.25 350.6 344.9 345. ]
print('h数据的最大值为: {}'.format(np.max(h)))
print('l数据的最小值为: {}'.format(np.min(l)))
h数据的最大值为: 364.9
l数据的最小值为: 333.53
NumPy中有一个ptp函数可以计算数组的取值范围
该函数返回的是数组元素的最大值和最小值之间的差值
也就是说,返回值等于max(array) - min(array)
print('h数据的最大值-最小值的差值为: \n{}'.format(np.ptp(h)))
print('l数据的最大值-最小值的差值为: \n{}'.format(np.ptp(l)))
h数据的最大值-最小值的差值为:
24.859999999999957
l数据的最大值-最小值的差值为:
26.970000000000027In der akademischen Literatur basiert die Analyse von Schlusskursen häufig auf Aktienrenditen und logarithmischen Renditen.
Die einfache Rendite bezieht sich auf die Änderungsrate zwischen zwei benachbarten Preisen, während sich die logarithmische Rendite auf die Differenz zwischen beiden nach Logarithmierung aller Preise bezieht.
Wir haben in der High School etwas über Logarithmen gelernt. Der Logarithmus von „a“ minus dem Logarithmus von „b“ ist gleich dem Logarithmus von „a dividiert durch b“. Daher kann die logarithmische Rendite auch zur Messung der Preisänderungsrate verwendet werden. Beachten Sie, dass die Rendite dimensionslos ist, da sie ein Verhältnis ist, zum Beispiel dividieren wir US-Dollar durch US-Dollar (es können auch andere Währungseinheiten sein).m = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
print('m数据中的中位数为: {}'.format(np.median(m)))
m数据中的中位数为: 352.055
# 数组排序后,查找中位数
sorted_m = np.msort(m)
print('m数据排序: \n{}'.format(sorted_m))
N = len(c)
print('m数据中的中位数为: {}'.format((sorted_m[N//2]+sorted_m[(N-1)//2])/2))
m数据排序:
[336.1 338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5 346.67
348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21 354.54 355.2
355.36 355.76 356.85 358.16 358.3 359.18 359.56 359.9 360. 363.13]
m数据中的中位数为: 352.055
方差:
方差是指各个数据与所有数据算术平均数的离差平方和除以数据个数所得到的值。
print('variance =', np.var(m))
variance = 50.126517888888884
var_hand = np.mean((m-m.mean())**2)
print('var =', var_hand)
var = 50.126517888888884print ("Standard deviation =", np.std(returns))Im Allgemeinen sollten wir das Eingabearray überprüfen, um sicherzustellen, dass es keine Nullen und negativen Zahlen enthält. Andernfalls erhalten Sie eine Fehlermeldung. In unserem Beispiel ist der Aktienkurs jedoch immer positiv, sodass auf die Prüfung verzichtet werden kann.
(3) Wir dürften sehr daran interessiert sein, an welchen Handelstagen positive Renditen erzielt werden.
Nach Abschluss der vorherigen Schritte müssen wir dazu nur noch die Where-Funktion verwenden. Die Where-Funktion kann die Indexwerte aller Array-Elemente zurückgeben, die die Bedingungen gemäß den angegebenen Bedingungen erfüllen.
Geben Sie den folgenden Code ein:
posretindices = np.where(returns > 0) print "Indices with positive returns", posretindices 即可输出该数组中所有正值元素的索引。 Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)
(4) 在投资学中,波动率(volatility)是对价格变动的一种度量。历史波动率可以根据历史价格数据计算得出。计算历史波动率(如年波动率或月波动率)时,需要用到对数收益率。年波动率等于对数收益率的标准差除以其均值,再除以交易日倒数的平方根,通常交易日取252天。用std和mean函数来计算
代码如下所示:
annual_volatility = np.std(logreturns)/np.mean(logreturns) annual_volatility = annual_volatility / np.sqrt(1./252.)
(5) sqrt函数中的除法运算。在Python中,整数的除法和浮点数的除法运算机制不同(python3已修改该功能),我们必须使用浮点数才能得到正确的结果。与计算年波动率的方法类似,计算月波动率如下:
annual_volatility * np.sqrt(1./12.)
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
returns = np.diff(c)/c[:-1]
print('returns的标准差: {}'.format(np.std(returns)))
logreturns = np.diff(np.log(c))
posretindices = np.where(returns>0)
print('retruns中元素为正数的位置: \n{}'.format(posretindices))
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility/np.sqrt(1/252)
print('每年波动率: {}'.format(annual_volatility))
print('每月波动率:{}'.format(annual_volatility*np.sqrt(1/12)))
returns的标准差: 0.012922134436826306
retruns中元素为正数的位置:
(array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23,
25, 28], dtype=int64),)
每年波动率: 129.27478991115132
每月波动率:37.318417377317765Das obige ist der detaillierte Inhalt vonSo verwenden Sie NumPy in allgemeinen Python-Funktionen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




