Der automatische Beweis mathematischer Theoreme ist eine ursprüngliche Absicht der künstlichen Intelligenz und war schon immer ein Problem. Bisher haben Humanmathematiker zwei unterschiedliche Schreibweisen für Mathematik verwendet.
Der erste Weg ist ein Weg, den jeder kennt, nämlich die Verwendung natürlicher Sprache zur Beschreibung mathematischer Beweise. Der Großteil der Mathematik ist auf diese Weise verfasst, darunter auch Mathematiklehrbücher, Mathematikarbeiten usw.
Der zweite Typ heißt formale Mathematik. Hierbei handelt es sich um ein von Informatikern im letzten halben Jahrhundert entwickeltes Werkzeug zur Überprüfung mathematischer Beweise.
Es scheint heutzutage, dass Computer zur Verifizierung mathematischer Beweise verwendet werden können, dies jedoch nur mit speziell entwickelten Beweissprachen, die mit der von Mathematikern verwendeten Mischung aus mathematischer Notation und geschriebenem Text nicht umgehen können. Die Umwandlung mathematischer Probleme, die in natürlicher Sprache geschrieben sind, in formalen Code, damit Computer sie einfacher lösen können, kann dabei helfen, Maschinen zu bauen, die neue Entdeckungen in der Mathematik erforschen können. Dieser Vorgang wird Formalisierung genannt, und Autoformalisierung bezeichnet die Aufgabe, Mathematik automatisch aus der natürlichen Sprache in eine formale Sprache zu übersetzen.
Die Automatisierung formaler Beweise ist eine herausfordernde Aufgabe, und Deep-Learning-Methoden haben in diesem Bereich noch keinen großen Erfolg erzielt, hauptsächlich aufgrund der Knappheit formaler Daten. Tatsächlich ist der formale Beweis selbst sehr schwierig und nur wenige Experten können ihn leisten, was umfangreiche Annotationsbemühungen unrealistisch macht. Der größte Korpus formaler Beweise ist im Isabelle-Code geschrieben (Paulson, 1994) und ist weniger als 0,6 GB groß, also um Größenordnungen kleiner als häufig verwendete Datensätze in der Bildverarbeitung oder der Verarbeitung natürlicher Sprache. Um dem Mangel an formalen Beweisen entgegenzuwirken, wurde in früheren Studien vorgeschlagen, synthetische Daten, selbstüberwachtes oder verstärkendes Lernen zu verwenden, um zusätzliche formale Trainingsdaten zu synthetisieren. Obwohl diese Methoden den Mangel an Daten bis zu einem gewissen Grad lindern, können sie die große Anzahl manuell geschriebener mathematischer Beweise nicht vollständig nutzen.
Nehmen wir als Beispiel das Sprachmodell Minerva. Nachdem wir mit genügend Daten trainiert hatten, stellten wir fest, dass seine mathematischen Fähigkeiten sehr stark sind und dass er in Mathematiktests an weiterführenden Schulen überdurchschnittliche Ergebnisse erzielen kann. Ein solches Sprachmodell weist jedoch auch Mängel auf. Es kann die Mathematik nur nachahmen, aber nicht unabhängig trainieren. Formale Beweissysteme bieten eine Trainingsumgebung, für die formale Mathematik liegen jedoch nur sehr wenige Daten vor.
Im Gegensatz zur formalen Mathematik sind informelle mathematische Daten reichlich vorhanden und allgemein verfügbar. In jüngster Zeit haben große Sprachmodelle, die auf informellen mathematischen Daten trainiert wurden, beeindruckende Fähigkeiten zum quantitativen Denken gezeigt. Allerdings liefern sie häufig fehlerhafte Beweise, und die automatische Erkennung fehlerhafter Argumente in diesen Beweisen ist eine Herausforderung.
In einer aktuellen Arbeit haben Forscher wie Yuhuai Tony Wu von Google eine neue Methode namens DSP (Draft, Sketch, and Prove) entwickelt, um informelle mathematische Beweise in formelle Beweise umzuwandeln Systeme und eine große Menge informeller Daten.
Link zum Papier: https://arxiv.org/pdf/2210.12283.pdf
Anfang dieses Jahres nutzten Wu Yuhuai und mehrere Mitarbeiter das neuronale Netzwerk von OpenAI Codex, um eine automatische Ausführung zu ermöglichen Formalisierungsarbeiten durchführen und die Machbarkeit der Verwendung großer Sprachmodelle zur automatischen Übersetzung informeller Aussagen in formale Aussagen beweisen. DSP geht noch einen Schritt weiter und nutzt große Sprachmodelle, um aus informellen Beweisen formale Beweisskizzen zu generieren. Beweisskizzen bestehen aus hochrangigen Argumentationsschritten, die von einem formalen System wie einem interaktiven Theorembeweiser interpretiert werden können. Sie unterscheiden sich von vollständigen formalen Beweisen dadurch, dass sie Folgen ungerechtfertigter Zwischenvermutungen enthalten. Im letzten Schritt des DSP wird die formale Beweisskizze zu einem vollständigen formalen Beweis ausgearbeitet, wobei ein automatischer Verifizierer zum Beweis aller Zwischenvermutungen verwendet wird.
Wu Yuhuai sagte: Jetzt zeigen wir, dass LLM die von ihm generierten informellen Beweise in verifizierte formale Beweise umwandeln kann!
Der Abschnitt „Methoden“ beschreibt einen DSP-Ansatz für die formale Beweisautomatisierung, der informelle Beweise als Leitfaden für Beweisskizzen für automatisierte formale Theorembeweiser verwendet. Dabei wird davon ausgegangen, dass es für jedes Problem einen informellen Satz und einen formellen Satz gibt, der das Problem beschreibt. Die Gesamtpipeline besteht aus drei Stufen (dargestellt in Abbildung 1).
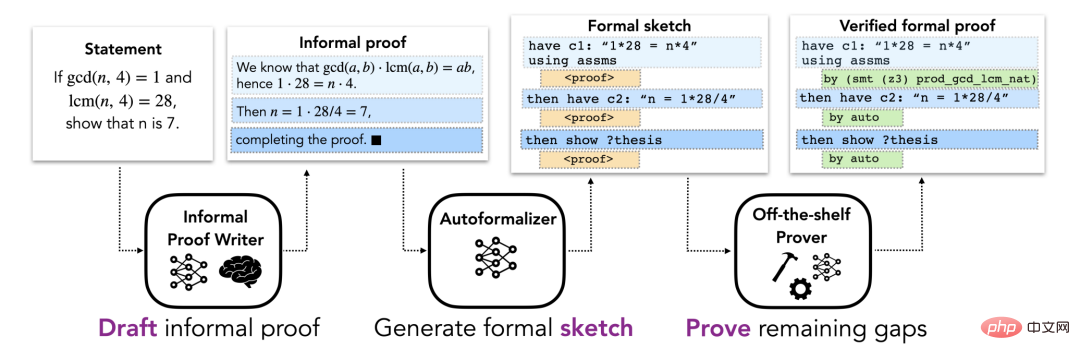
Abbildung 1.
Die Anfangsphase des DSP-Ansatzes, einschließlich der Suche nach einer informellen Form für das Problem basierend auf seiner natürlichen mathematischen Sprachbeschreibung (möglicherweise). mit LATEX-Beweis. Der resultierende informelle Beweis wird als Rohentwurf für nachfolgende Phasen behandelt. In Mathematiklehrbüchern werden in der Regel Beweise für Theoreme aufgeführt, manchmal fehlen sie jedoch oder sind unvollständig. Daher betrachteten die Forscher zwei Situationen, die dem Vorhandensein oder Fehlen informeller Beweise entsprechen.
Im ersten Fall geht der Forscher davon aus, dass es einen „echten“ informellen Beweis (also einen von einem Menschen verfassten Beweis) gibt, was eine typische Situation in der formalen Praxis bestehender mathematischer Theorien darstellt. Im zweiten Fall gehen die Forscher von einer allgemeineren Annahme aus, dass kein echter informeller Beweis erbracht wird, und verwenden ein umfangreiches Sprachmodell, das auf informellen mathematischen Daten trainiert wurde, um Beweiskandidaten zu entwerfen. Das Sprachmodell macht die Abhängigkeit von menschlichen Beweisen überflüssig und kann für jedes Problem mehrere alternative Lösungen generieren. Obwohl es keine einfache Möglichkeit gibt, die Korrektheit dieser Beweise automatisch zu überprüfen, müssen informelle Beweise erst im nächsten Schritt bei der Erstellung einer guten formalen Beweisskizze nützlich sein.
Formelle Beweisskizzen verschlüsseln die Struktur einer Lösung und lassen Details auf niedriger Ebene außer Acht. Intuitiv handelt es sich um einen Teilbeweis, der eine hochrangige Vermutungsaussage umreißt. Abbildung 2 ist ein konkretes Beispiel einer Beweisskizze. Obwohl in informellen Beweisen häufig Details auf niedriger Ebene außer Acht gelassen werden, können diese Details in formellen Beweisen nicht ausgeschlossen werden, was die direkte Umwandlung informeller Beweise in formale Beweise schwierig macht. Stattdessen schlägt dieses Papier vor, informelle Beweise auf formale Beweisskizzen abzubilden, die dieselbe übergeordnete Struktur aufweisen. Details auf niedriger Ebene, die in der Beweisskizze fehlen, können vom automatischen Prüfer ergänzt werden. Da große informell-formale Parallelkorpora nicht existieren, sind Standardmethoden der maschinellen Übersetzung für diese Aufgabe nicht geeignet. Stattdessen werden hier die Fear-Shot-Lernfähigkeiten eines großen Sprachmodells genutzt. Insbesondere werden einige Beispielpaare, die informelle Beweise und ihre entsprechenden formalen Skizzen enthalten, verwendet, um das Modell aufzufordern, gefolgt von einem informellen Beweis, der konvertiert werden soll, und das Modell dann nachfolgende Token generieren zu lassen, um die erforderliche formale Skizze zu erhalten. Dieses Modell wird als „automatischer Formalisierer“ bezeichnet.
Abbildung 2. Offene Vermutung in der Beweisskizze Ein „automatischer Beweiser“ bezieht sich hier auf ein System, das formal überprüfbare Beweise liefern kann. Das Framework ist unabhängig von der spezifischen Wahl des automatischen Beweisers: Es kann sich um einen symbolischen Beweiser (z. B. ein Automatisierungstool für heuristische Beweise), einen auf einem neuronalen Netzwerk basierenden Beweiser oder einen Hybridansatz handeln. Wenn der automatische Beweiser alle Lücken in der Beweisskizze erfolgreich füllt, liefert er einen endgültigen formalen Beweis zurück, der anhand der Spezifikation des Problems überprüft werden kann. Wenn der automatische Prüfer fehlschlägt (z. B. weil das zugewiesene Zeitlimit überschritten wird), gilt die Bewertung als nicht erfolgreich.
Die Forscher führten eine Reihe von Experimenten durch, darunter formale Beweise für Probleme, die aus dem miniF2F-Datensatz generiert wurden, und zeigten, dass ein großer Teil der Theoreme mit dieser Methode automatisch bewiesen werden kann. Hier werden zwei Umgebungen untersucht, in denen informelle Beweise von Menschen geschrieben oder von einem großen Sprachmodell entworfen werden, das auf mathematischen Texten trainiert wird. Diese beiden Einstellungen entsprechen Situationen, die häufig bei der Formalisierung bestehender Theorien auftreten, das heißt, es gibt häufig informelle Beweise, die jedoch manchmal dem Leser als Übung überlassen werden oder aufgrund von Einschränkungen am Rand fehlen.
Tabelle 1 zeigt den Anteil erfolgreicher formaler Beweise, die im miniF2F-Datensatz gefunden wurden. Die Ergebnisse umfassen vier Basislinien aus unseren Experimenten sowie die DSP-Methode mit von Menschen geschriebenen Beweisen und modellgenerierten Beweisen.
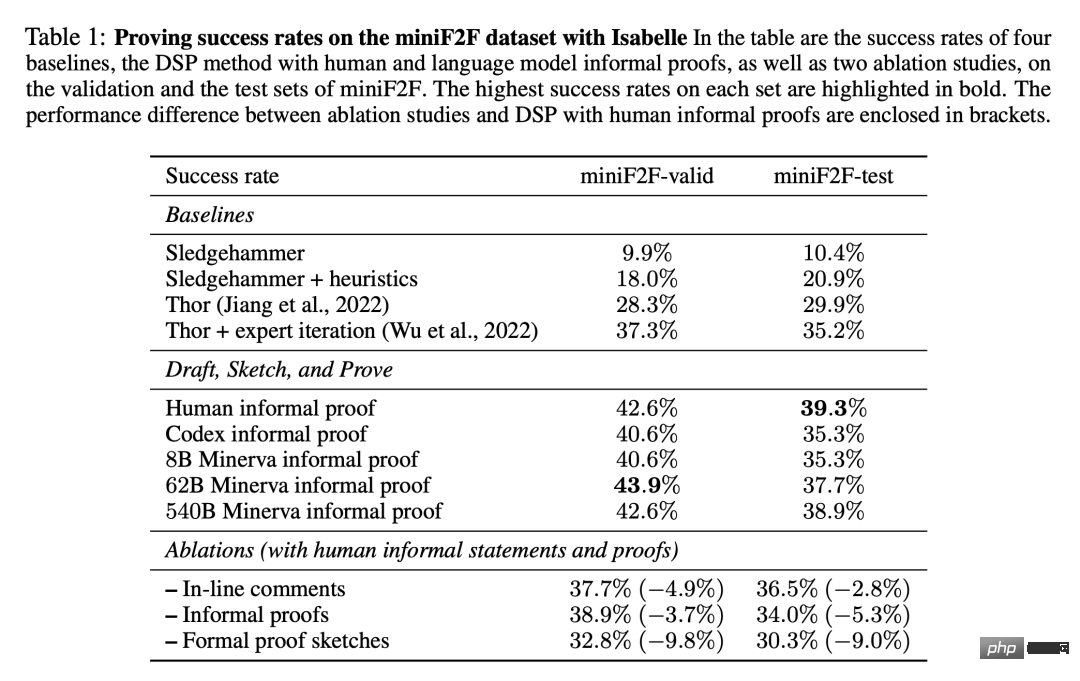
Es ist ersichtlich, dass der automatische Prüfer mit 11 angehängten Heuristikstrategien die Leistung von Sledgehammer erheblich steigert und seine Erfolgsquote beim Verifizierungssatz von miniF2F im Testsatz erhöht , stieg sie von 10,4 % auf 20,9 %. Zwei Baselines, die Sprachmodelle und Beweissuche verwendeten, erzielten im Testsatz von miniF2F Erfolgsraten von 29,9 % bzw. 35,2 %.
Basierend auf informellen Beweisen, die von Menschen verfasst wurden, erreicht die DSP-Methode Erfolgsraten von 42,6 % und 39,3 % bei den Validierungs- und Testsätzen von miniF2F. Insgesamt lassen sich auf diese Weise 200 der 488 Probleme beweisen. Das Codex-Modell und das Minerva-Modell (8B) lieferten bei der Lösung von Problemen auf miniF2F sehr ähnliche Ergebnisse: Beide führten den automatischen Prüfer dazu, 40,6 % bzw. 35,3 % der Probleme im Validierungs- und Testsatz zu lösen.
Beim Wechsel zum Modell Minerva (62B) stiegen die Erfolgsquoten auf 43,9 % bzw. 37,7 %. Im Vergleich zu von Menschen verfassten informellen Beweisen ist die Erfolgsquote beim Validierungssatz um 1,3 % höher und beim Testsatz um 1,6 % niedriger. Insgesamt konnte das Minerva-Modell (62B) 199 Probleme auf miniF2F lösen, eins weniger als ein von Menschen geschriebener Beweis. Das Minerva-Modell (540B) löste 42,6 % bzw. 38,9 % der Probleme im Validierungssatz und Testsatz von miniF2F und generierte außerdem 199 erfolgreiche Beweise.
DSP-Methoden leiten automatische Beweiser in beiden Fällen effektiv: informelle Beweise durch Menschen oder informelle Beweise, die durch Sprachmodelle generiert werden. DSP hat die Erfolgsquote des Prüfers fast verdoppelt und mit Isabelle SOTA-Leistung auf miniF2F erzielt. Darüber hinaus sind größere Minerva-Modelle bei der Anleitung automatisierter formaler Prüfer fast genauso hilfreich wie Menschen.
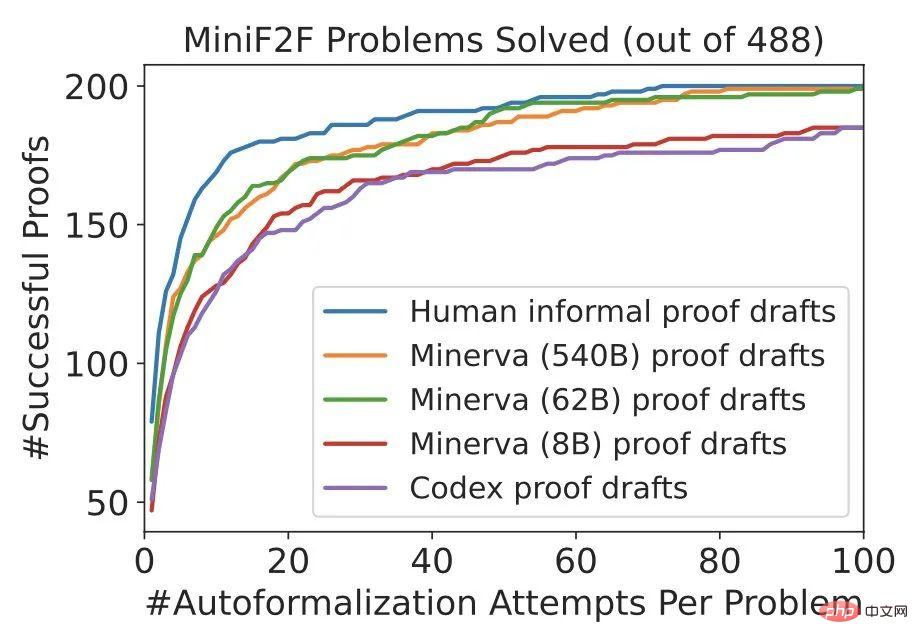
Wie in der Abbildung unten gezeigt, verbessert die DSP-Methode die Leistung des Sledgehammer + heuristischen Prüfers erheblich (~20 % -> ~40 %), wodurch ein neuer SOTA auf miniF2F erreicht wird.
Die 62B- und 540B-Versionen von Minerva erzeugen Beweise, die menschlichen Beweisen sehr ähnlich sind.
Weitere Informationen finden Sie im Originalpapier.
Das obige ist der detaillierte Inhalt vonKI mischt erneut in der Welt der Mathematik mit und neue DSP-Methoden verdoppeln die Erfolgsquote maschineller Beweise. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
