So verwenden Sie eine Adjazenzliste zum Speichern von Diagrammen in Java
1. Der letzte Schliff
Die Adjazenzliste ist eine verknüpfte Speichermethode für Diagramme. Ihre Datenstruktur besteht aus zwei Teilen: Knoten und Adjazenzpunkten.
Adjazenzlisten können zur Darstellung ungerichteter Graphen, gerichteter Graphen und Netzwerke verwendet werden. Dies wird anhand eines ungerichteten Graphen erklärt.
1. Ungerichteter Graph
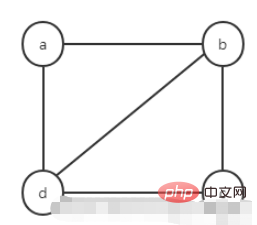
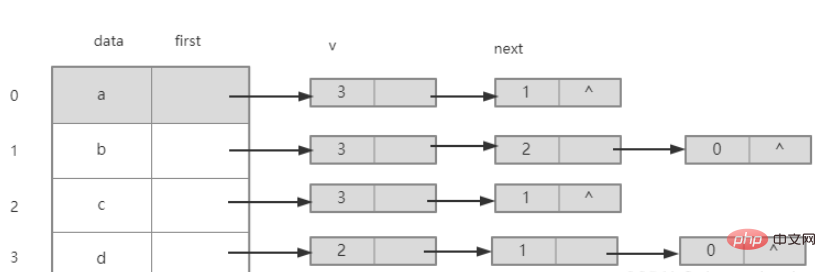
2. Linktabelle des ungerichteten Graphen
# 🎜🎜 #

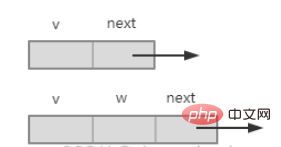
package graph;
import java.util.Scanner;
public class CreateALGraph {
static final int MaxVnum = 100; // 顶点数最大值
public static void main(String[] args) {
ALGraph G = new ALGraph();
for (int i = 0; i < G.Vex.length; i++) {
G.Vex[i] = new VexNode();
}
CreateALGraph(G); // 创建有向图邻接表
printg(G); // 输出邻接表
}
static int locatevex(ALGraph G, char x) {
for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
if (x == G.Vex[i].data)
return i;
return -1; // 没找到
}
// 插入一条边
static void insertedge(ALGraph G, int i, int j) {
AdjNode s = new AdjNode();
s.v = j;
s.next = G.Vex[i].first;
G.Vex[i].first = s;
}
// 输出邻接表
static void printg(ALGraph G) {
System.out.println("----------邻接表如下:----------");
for (int i = 0; i < G.vexnum; i++) {
AdjNode t = G.Vex[i].first;
System.out.print(G.Vex[i].data + ": ");
while (t != null) {
System.out.print("[" + t.v + "]\t");
t = t.next;
}
System.out.println();
}
}
// 创建有向图邻接表
static void CreateALGraph(ALGraph G) {
int i, j;
char u, v;
System.out.println("请输入顶点数和边数:");
Scanner scanner = new Scanner(System.in);
G.vexnum = scanner.nextInt();
G.edgenum = scanner.nextInt();
System.out.println("请输入顶点信息:");
for (i = 0; i < G.vexnum; i++)//输入顶点信息,存入顶点信息数组
G.Vex[i].data = scanner.next().charAt(0);
for (i = 0; i < G.vexnum; i++)
G.Vex[i].first = null;
System.out.println("请依次输入每条边的两个顶点u,v");
while (G.edgenum-- > 0) {
u = scanner.next().charAt(0);
v = scanner.next().charAt(0);
i = locatevex(G, u); // 查找顶点 u 的存储下标
j = locatevex(G, v); // 查找顶点 v 的存储下标
if (i != -1 && j != -1)
insertedge(G, i, j);
else {
System.out.println("输入顶点信息错!请重新输入!");
G.edgenum++; // 本次输入不算
}
}
}
}
// 定义邻接点类型
class AdjNode {
int v; // 邻接点下标
AdjNode next; // 指向下一个邻接点
}
// 定义顶点类型
class VexNode {
char data; // VexType为顶点的数据类型,根据需要定义
AdjNode first; // 指向第一个邻接点
}
// 定义邻接表类型
class ALGraph {
VexNode Vex[] = new VexNode[CreateALGraph.MaxVnum];
int vexnum; // 顶点数
int edgenum; // 边数
}Nach dem Login kopieren
5.TestWeiß ist Ausgabe, Grün ist Eingabepackage graph;
import java.util.Scanner;
public class CreateALGraph {
static final int MaxVnum = 100; // 顶点数最大值
public static void main(String[] args) {
ALGraph G = new ALGraph();
for (int i = 0; i < G.Vex.length; i++) {
G.Vex[i] = new VexNode();
}
CreateALGraph(G); // 创建有向图邻接表
printg(G); // 输出邻接表
}
static int locatevex(ALGraph G, char x) {
for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
if (x == G.Vex[i].data)
return i;
return -1; // 没找到
}
// 插入一条边
static void insertedge(ALGraph G, int i, int j) {
AdjNode s = new AdjNode();
s.v = j;
s.next = G.Vex[i].first;
G.Vex[i].first = s;
}
// 输出邻接表
static void printg(ALGraph G) {
System.out.println("----------邻接表如下:----------");
for (int i = 0; i < G.vexnum; i++) {
AdjNode t = G.Vex[i].first;
System.out.print(G.Vex[i].data + ": ");
while (t != null) {
System.out.print("[" + t.v + "]\t");
t = t.next;
}
System.out.println();
}
}
// 创建有向图邻接表
static void CreateALGraph(ALGraph G) {
int i, j;
char u, v;
System.out.println("请输入顶点数和边数:");
Scanner scanner = new Scanner(System.in);
G.vexnum = scanner.nextInt();
G.edgenum = scanner.nextInt();
System.out.println("请输入顶点信息:");
for (i = 0; i < G.vexnum; i++)//输入顶点信息,存入顶点信息数组
G.Vex[i].data = scanner.next().charAt(0);
for (i = 0; i < G.vexnum; i++)
G.Vex[i].first = null;
System.out.println("请依次输入每条边的两个顶点u,v");
while (G.edgenum-- > 0) {
u = scanner.next().charAt(0);
v = scanner.next().charAt(0);
i = locatevex(G, u); // 查找顶点 u 的存储下标
j = locatevex(G, v); // 查找顶点 v 的存储下标
if (i != -1 && j != -1)
insertedge(G, i, j);
else {
System.out.println("输入顶点信息错!请重新输入!");
G.edgenum++; // 本次输入不算
}
}
}
}
// 定义邻接点类型
class AdjNode {
int v; // 邻接点下标
AdjNode next; // 指向下一个邻接点
}
// 定义顶点类型
class VexNode {
char data; // VexType为顶点的数据类型,根据需要定义
AdjNode first; // 指向第一个邻接点
}
// 定义邻接表类型
class ALGraph {
VexNode Vex[] = new VexNode[CreateALGraph.MaxVnum];
int vexnum; // 顶点数
int edgenum; // 边数
}#
Das obige ist der detaillierte Inhalt vonSo verwenden Sie eine Adjazenzliste zum Speichern von Diagrammen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur Smith-Zahl in Java. Hier besprechen wir die Definition: Wie überprüft man die Smith-Nummer in Java? Beispiel mit Code-Implementierung.
 Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
In diesem Artikel haben wir die am häufigsten gestellten Fragen zu Java Spring-Interviews mit ihren detaillierten Antworten zusammengestellt. Damit Sie das Interview knacken können.
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Java 8 führt die Stream -API ein und bietet eine leistungsstarke und ausdrucksstarke Möglichkeit, Datensammlungen zu verarbeiten. Eine häufige Frage bei der Verwendung von Stream lautet jedoch: Wie kann man von einem Foreach -Betrieb brechen oder zurückkehren? Herkömmliche Schleifen ermöglichen eine frühzeitige Unterbrechung oder Rückkehr, aber die Stream's foreach -Methode unterstützt diese Methode nicht direkt. In diesem Artikel werden die Gründe erläutert und alternative Methoden zur Implementierung vorzeitiger Beendigung in Strahlverarbeitungssystemen erforscht. Weitere Lektüre: Java Stream API -Verbesserungen Stream foreach verstehen Die Foreach -Methode ist ein Terminalbetrieb, der einen Vorgang für jedes Element im Stream ausführt. Seine Designabsicht ist
 Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Anleitung zum TimeStamp to Date in Java. Hier diskutieren wir auch die Einführung und wie man Zeitstempel in Java in ein Datum konvertiert, zusammen mit Beispielen.
 Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Kapseln sind dreidimensionale geometrische Figuren, die aus einem Zylinder und einer Hemisphäre an beiden Enden bestehen. Das Volumen der Kapsel kann berechnet werden, indem das Volumen des Zylinders und das Volumen der Hemisphäre an beiden Enden hinzugefügt werden. In diesem Tutorial wird erörtert, wie das Volumen einer bestimmten Kapsel in Java mit verschiedenen Methoden berechnet wird. Kapselvolumenformel Die Formel für das Kapselvolumen lautet wie folgt: Kapselvolumen = zylindrisches Volumenvolumen Zwei Hemisphäre Volumen In, R: Der Radius der Hemisphäre. H: Die Höhe des Zylinders (ohne die Hemisphäre). Beispiel 1 eingeben Radius = 5 Einheiten Höhe = 10 Einheiten Ausgabe Volumen = 1570,8 Kubikeinheiten erklären Berechnen Sie das Volumen mithilfe der Formel: Volumen = π × R2 × H (4
 PHP vs. Python: Verständnis der Unterschiede
Apr 11, 2025 am 12:15 AM
PHP vs. Python: Verständnis der Unterschiede
Apr 11, 2025 am 12:15 AM
PHP und Python haben jeweils ihre eigenen Vorteile, und die Wahl sollte auf Projektanforderungen beruhen. 1.PHP eignet sich für die Webentwicklung mit einfacher Syntax und hoher Ausführungseffizienz. 2. Python eignet sich für Datenwissenschaft und maschinelles Lernen mit präziser Syntax und reichhaltigen Bibliotheken.
 PHP: Eine Schlüsselsprache für die Webentwicklung
Apr 13, 2025 am 12:08 AM
PHP: Eine Schlüsselsprache für die Webentwicklung
Apr 13, 2025 am 12:08 AM
PHP ist eine Skriptsprache, die auf der Serverseite weit verbreitet ist und insbesondere für die Webentwicklung geeignet ist. 1.PHP kann HTML einbetten, HTTP -Anforderungen und Antworten verarbeiten und eine Vielzahl von Datenbanken unterstützt. 2.PHP wird verwendet, um dynamische Webinhalte, Prozessformdaten, Zugriffsdatenbanken usw. mit starker Community -Unterstützung und Open -Source -Ressourcen zu generieren. 3. PHP ist eine interpretierte Sprache, und der Ausführungsprozess umfasst lexikalische Analyse, grammatikalische Analyse, Zusammenstellung und Ausführung. 4.PHP kann mit MySQL für erweiterte Anwendungen wie Benutzerregistrierungssysteme kombiniert werden. 5. Beim Debuggen von PHP können Sie Funktionen wie error_reporting () und var_dump () verwenden. 6. Optimieren Sie den PHP-Code, um Caching-Mechanismen zu verwenden, Datenbankabfragen zu optimieren und integrierte Funktionen zu verwenden. 7
 Gestalten Sie die Zukunft: Java-Programmierung für absolute Anfänger
Oct 13, 2024 pm 01:32 PM
Gestalten Sie die Zukunft: Java-Programmierung für absolute Anfänger
Oct 13, 2024 pm 01:32 PM
Java ist eine beliebte Programmiersprache, die sowohl von Anfängern als auch von erfahrenen Entwicklern erlernt werden kann. Dieses Tutorial beginnt mit grundlegenden Konzepten und geht dann weiter zu fortgeschrittenen Themen. Nach der Installation des Java Development Kit können Sie das Programmieren üben, indem Sie ein einfaches „Hello, World!“-Programm erstellen. Nachdem Sie den Code verstanden haben, verwenden Sie die Eingabeaufforderung, um das Programm zu kompilieren und auszuführen. Auf der Konsole wird „Hello, World!“ ausgegeben. Mit dem Erlernen von Java beginnt Ihre Programmierreise, und wenn Sie Ihre Kenntnisse vertiefen, können Sie komplexere Anwendungen erstellen.






