 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 So implementieren Sie das Tower of Hanoi-Problem mit Python
So implementieren Sie das Tower of Hanoi-Problem mit Python
So implementieren Sie das Tower of Hanoi-Problem mit Python
Vorwort
Das Problem des Turms von Hanoi ist ein klassisches Problem. Der Hanoi-Turm, auch Hanoi-Turm genannt, geht auf eine alte Legende in Indien zurück. Als Brahma die Welt erschuf, schuf er drei Diamantsäulen. Auf einer Säule wurden 64 Goldscheiben in der Reihenfolge ihrer Größe von unten nach oben gestapelt. Brahma befahl dem Brahmin, die Scheiben auf einer anderen Säule in der Reihenfolge ihrer Größe von unten neu anzuordnen. Es ist auch festgelegt, dass die Scheibe zu keinem Zeitpunkt auf der kleinen Scheibe vergrößert werden kann und jeweils nur eine Scheibe zwischen den drei Säulen bewegt werden kann. Fragen Sie, wie man funktioniert?
1. Lassen Sie uns zunächst darüber sprechen, was Rekursion ist.
Mein eigenes Verständnis ist: Reduzieren Sie weiterhin die Größe Ihrer eigenen Probleme, bis sie so weit reduziert sind, dass sie nicht mehr reduziert werden können. (Die Endbedingung der Rekursion ist erreicht) Beginnen Sie dann mit der Lösung der kleinen Probleme, nachdem Sie die kleinen Probleme einzeln gelöst haben (die Rekursion ist zurück)
2. Kurz gesagt:
Das ursprüngliche Problem wird kontinuierlich auf einen kleineren Maßstab des ursprünglichen Problems reduziert, und dann wird das kleine ursprüngliche Problem gelöst, wodurch das ursprüngliche große Problem gelöst wird!
3. Der Prozess ist:
Reduzieren Sie den Maßstab, lösen Sie ihn von einer kleinen Größe, rekursieren Sie zurück und lösen Sie das ursprüngliche Problem! ! !
4. Der Schlüssel zur Rekursion ist:
(1) Es gibt eine Rekursionsendbedingung.
(2) Ruft sich ständig auf, um die Größe des Problems zu verringern und näher an die Endbedingung der Rekursion heranzukommen.
Problem mit dem Turm von Hanoi
1. Problembeschreibung
Es gibt drei Säulen mit den Namen A, B und C. Zu Beginn gibt es n Scheiben auf der Säule A, sie sind von unten nach oben und die Größe der Scheiben reicht von groß nach klein. Beim Bewegen und Platzieren müssen die kleinen Platten auf den großen Platten liegen. Verschieben Sie unter Beachtung der Regeln alle Platten der Säule A zur Säule C. Sie können während des Umzugs die Säule B nutzen, müssen aber darauf achten, dass die kleinen Platten während des Umzugs auf den großen Platten liegen müssen! ! ! Bitte den Umzugsvorgang ausdrucken?
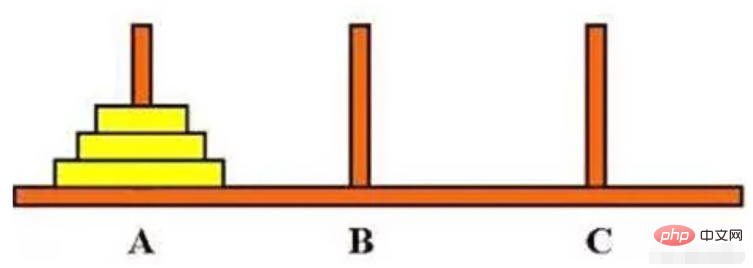
2. Rekursiver Prozess der Problemanalyse:
(1) Verschieben Sie die oberen n-1 Platten mit Hilfe von C
(2) Verschieben Sie die untere Platte von A nach C
(3 ) Verschieben Sie die oberen n-1 Platten mit Hilfe von A von B nach C
Die Endbedingung der Rekursion:
Die Problemskala wird, wenn die Anzahl der Platten 0 ist, denn wenn die Anzahl der Platten 0 ist, ist dies nicht erforderlich umziehen! ! !
3. Code (Python)
# coding:utf-8
"""
n为初始时A柱上的盘子数
a为起始盘子所在的柱子
b为中转柱子
c为目的地柱子
"""
def hanoi(n, a, b, c):
if n > 0:
hanoi(n-1, a, c, b)
print("盘子从%s移动到%s" % (a, c))
hanoi(n-1, b, a, c)
hanoi(3, "A", "B", "C")4
Das obige ist der detaillierte Inhalt vonSo implementieren Sie das Tower of Hanoi-Problem mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Wie kontrolliert PS -Federn die Weichheit des Übergangs?
Apr 06, 2025 pm 07:33 PM
Wie kontrolliert PS -Federn die Weichheit des Übergangs?
Apr 06, 2025 pm 07:33 PM
Der Schlüssel zur Federkontrolle liegt darin, seine allmähliche Natur zu verstehen. PS selbst bietet nicht die Möglichkeit, die Gradientenkurve direkt zu steuern, aber Sie können den Radius und die Gradientenweichheit flexius durch mehrere Federn, Matching -Masken und feine Selektionen anpassen, um einen natürlichen Übergangseffekt zu erzielen.
 Muss MySQL bezahlen?
Apr 08, 2025 pm 05:36 PM
Muss MySQL bezahlen?
Apr 08, 2025 pm 05:36 PM
MySQL hat eine kostenlose Community -Version und eine kostenpflichtige Enterprise -Version. Die Community -Version kann kostenlos verwendet und geändert werden, die Unterstützung ist jedoch begrenzt und für Anwendungen mit geringen Stabilitätsanforderungen und starken technischen Funktionen geeignet. Die Enterprise Edition bietet umfassende kommerzielle Unterstützung für Anwendungen, die eine stabile, zuverlässige Hochleistungsdatenbank erfordern und bereit sind, Unterstützung zu bezahlen. Zu den Faktoren, die bei der Auswahl einer Version berücksichtigt werden, gehören Kritikalität, Budgetierung und technische Fähigkeiten von Anwendungen. Es gibt keine perfekte Option, nur die am besten geeignete Option, und Sie müssen die spezifische Situation sorgfältig auswählen.
 So verwenden Sie MySQL nach der Installation
Apr 08, 2025 am 11:48 AM
So verwenden Sie MySQL nach der Installation
Apr 08, 2025 am 11:48 AM
Der Artikel führt den Betrieb der MySQL -Datenbank vor. Zunächst müssen Sie einen MySQL -Client wie MySQLworkBench oder Befehlszeilen -Client installieren. 1. Verwenden Sie den Befehl mySQL-uroot-P, um eine Verbindung zum Server herzustellen und sich mit dem Stammkonto-Passwort anzumelden. 2. Verwenden Sie die Erstellung von Createdatabase, um eine Datenbank zu erstellen, und verwenden Sie eine Datenbank aus. 3.. Verwenden Sie CreateTable, um eine Tabelle zu erstellen, Felder und Datentypen zu definieren. 4. Verwenden Sie InsertInto, um Daten einzulegen, Daten abzufragen, Daten nach Aktualisierung zu aktualisieren und Daten nach Löschen zu löschen. Nur indem Sie diese Schritte beherrschen, lernen, mit gemeinsamen Problemen umzugehen und die Datenbankleistung zu optimieren, können Sie MySQL effizient verwenden.
 Wie richte ich PS -Federn ein?
Apr 06, 2025 pm 07:36 PM
Wie richte ich PS -Federn ein?
Apr 06, 2025 pm 07:36 PM
PS Federn ist ein Bildkantenschwärcheneffekt, der durch den gewichteten Durchschnitt der Pixel im Randbereich erreicht wird. Das Einstellen des Federradius kann den Grad der Unschärfe steuern und je größer der Wert ist, desto unscharfer ist er. Eine flexible Einstellung des Radius kann den Effekt entsprechend den Bildern und Bedürfnissen optimieren. Verwenden Sie beispielsweise einen kleineren Radius, um Details bei der Verarbeitung von Charakterfotos zu erhalten und einen größeren Radius zu verwenden, um ein dunstiges Gefühl bei der Verarbeitung von Kunst zu erzeugen. Es ist jedoch zu beachten, dass zu groß der Radius leicht an Kantendetails verlieren kann, und zu klein ist der Effekt nicht offensichtlich. Der Federneffekt wird von der Bildauflösung beeinflusst und muss anhand des Bildverständnisses und des Griffs von Effekten angepasst werden.
 MySQL kann nach dem Herunterladen nicht installiert werden
Apr 08, 2025 am 11:24 AM
MySQL kann nach dem Herunterladen nicht installiert werden
Apr 08, 2025 am 11:24 AM
Die Hauptgründe für den Fehler bei MySQL -Installationsfehlern sind: 1. Erlaubnisprobleme, Sie müssen als Administrator ausgeführt oder den Sudo -Befehl verwenden. 2. Die Abhängigkeiten fehlen, und Sie müssen relevante Entwicklungspakete installieren. 3. Portkonflikte müssen Sie das Programm schließen, das Port 3306 einnimmt, oder die Konfigurationsdatei ändern. 4. Das Installationspaket ist beschädigt. Sie müssen die Integrität herunterladen und überprüfen. 5. Die Umgebungsvariable ist falsch konfiguriert und die Umgebungsvariablen müssen korrekt entsprechend dem Betriebssystem konfiguriert werden. Lösen Sie diese Probleme und überprüfen Sie jeden Schritt sorgfältig, um MySQL erfolgreich zu installieren.
 So optimieren Sie die Datenbankleistung nach der MySQL -Installation
Apr 08, 2025 am 11:36 AM
So optimieren Sie die Datenbankleistung nach der MySQL -Installation
Apr 08, 2025 am 11:36 AM
Die MySQL -Leistungsoptimierung muss von drei Aspekten beginnen: Installationskonfiguration, Indexierung und Abfrageoptimierung, Überwachung und Abstimmung. 1. Nach der Installation müssen Sie die my.cnf -Datei entsprechend der Serverkonfiguration anpassen, z. 2. Erstellen Sie einen geeigneten Index, um übermäßige Indizes zu vermeiden und Abfrageanweisungen zu optimieren, z. B. den Befehl Erklärung zur Analyse des Ausführungsplans; 3. Verwenden Sie das eigene Überwachungstool von MySQL (ShowProcessList, Showstatus), um die Datenbankgesundheit zu überwachen und die Datenbank regelmäßig zu sichern und zu organisieren. Nur durch kontinuierliche Optimierung dieser Schritte kann die Leistung der MySQL -Datenbank verbessert werden.
 Die MySQL -Download -Datei ist beschädigt und kann nicht installiert werden. Reparaturlösung
Apr 08, 2025 am 11:21 AM
Die MySQL -Download -Datei ist beschädigt und kann nicht installiert werden. Reparaturlösung
Apr 08, 2025 am 11:21 AM
Die MySQL -Download -Datei ist beschädigt. Was soll ich tun? Wenn Sie MySQL herunterladen, können Sie die Korruption der Datei begegnen. Es ist heutzutage wirklich nicht einfach! In diesem Artikel wird darüber gesprochen, wie dieses Problem gelöst werden kann, damit jeder Umwege vermeiden kann. Nach dem Lesen können Sie nicht nur das beschädigte MySQL -Installationspaket reparieren, sondern auch ein tieferes Verständnis des Download- und Installationsprozesses haben, um zu vermeiden, dass Sie in Zukunft stecken bleiben. Lassen Sie uns zunächst darüber sprechen, warum das Herunterladen von Dateien beschädigt wird. Dafür gibt es viele Gründe. Netzwerkprobleme sind der Schuldige. Unterbrechung des Download -Prozesses und der Instabilität im Netzwerk kann zu einer Korruption von Dateien führen. Es gibt auch das Problem mit der Download -Quelle selbst. Die Serverdatei selbst ist gebrochen und natürlich auch unterbrochen, wenn Sie sie herunterladen. Darüber hinaus kann das übermäßige "leidenschaftliche" Scannen einer Antiviren -Software auch zu einer Beschädigung von Dateien führen. Diagnoseproblem: Stellen Sie fest, ob die Datei wirklich beschädigt ist
 Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Die MySQL-Datenbankleistung Optimierungshandbuch In ressourcenintensiven Anwendungen spielt die MySQL-Datenbank eine entscheidende Rolle und ist für die Verwaltung massiver Transaktionen verantwortlich. Mit der Erweiterung der Anwendung werden jedoch die Datenbankleistung Engpässe häufig zu einer Einschränkung. In diesem Artikel werden eine Reihe effektiver Strategien zur Leistungsoptimierung von MySQL -Leistung untersucht, um sicherzustellen, dass Ihre Anwendung unter hohen Lasten effizient und reaktionsschnell bleibt. Wir werden tatsächliche Fälle kombinieren, um eingehende Schlüsseltechnologien wie Indexierung, Abfrageoptimierung, Datenbankdesign und Caching zu erklären. 1. Das Design der Datenbankarchitektur und die optimierte Datenbankarchitektur sind der Eckpfeiler der MySQL -Leistungsoptimierung. Hier sind einige Kernprinzipien: Die Auswahl des richtigen Datentyps und die Auswahl des kleinsten Datentyps, der den Anforderungen entspricht, kann nicht nur Speicherplatz speichern, sondern auch die Datenverarbeitungsgeschwindigkeit verbessern.



