So erstellen Sie einen Heap von Java-Datenstrukturen

Eigenschaften des Heaps

Der Heap ist logischerweise ein vollständiger Binärbaum und der Heap wird physisch in einem Array gespeichert.

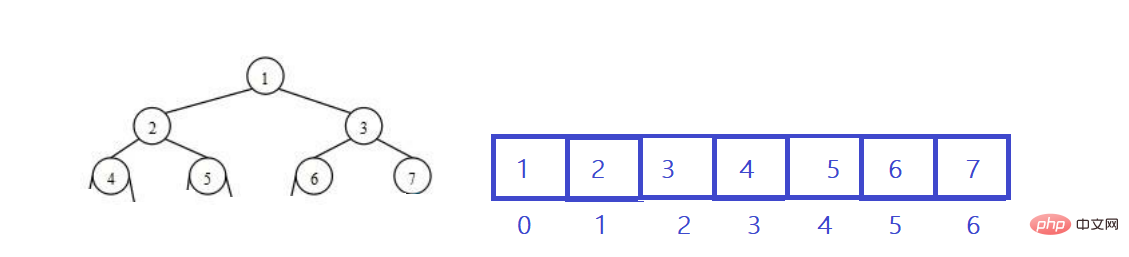
Zusammenfassung: Ein vollständiger Binärbaum wird mithilfe von Level-Order-Traversal in einem Array gespeichert. Die Hauptverwendung dieser Methode ist die Heap-Darstellung.

Und wenn der Index des übergeordneten Elements bekannt ist,

dann: Index des linken Kindes (links) = 2 * Eltern + 1;

Index des rechten Kindes (rechts) = 2 * Eltern + 2;

Das ist bekannt Der Index des untergeordneten Elements (ohne zwischen links und rechts zu unterscheiden) lautet:

Parent (parent) subscript = (child - 1) / 2;

Klassifizierung von Heaps

Großer Heap: Der Wurzelknoten ist größer als der linke und rechte untergeordnete Knoten Ein vollständiger Binärbaum (der übergeordnete Knoten ist größer als sein untergeordneter Knoten) wird als großer Heap, großer Root-Heap oder maximaler Heap bezeichnet.

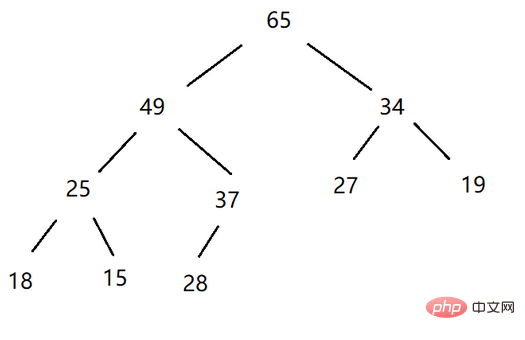
Kleiner Heap: Ein vollständiger Binärbaum, dessen Wurzelknoten kleiner ist als seine beiden linken und rechten untergeordneten Knoten, wird als kleiner Heap (der übergeordnete Knoten ist kleiner als seine untergeordneten Knoten) oder kleiner Wurzelheap oder a bezeichnet minimaler Haufen.

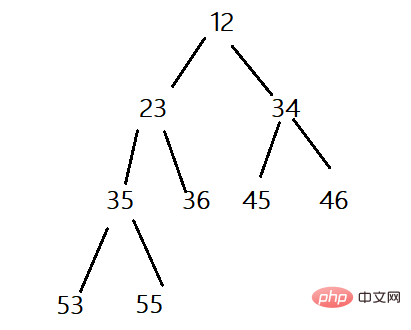
Abwärtsanpassung des Heaps

Jetzt gibt es ein Array, das logischerweise ein vollständiger Binärbaum ist. Wir können es durch den Abwärtsanpassungsalgorithmus ausgehend vom Wurzelknoten in einen kleinen Heap oder einen großen Heap anpassen. Der Abwärtsanpassungsalgorithmus hat eine Prämisse: Der linke und der rechte Teilbaum müssen ein Heap sein, bevor sie angepasst werden können.

Nehmen Sie einen kleinen Heap als Beispiel:

1 Lassen Sie zunächst den linken und rechten untergeordneten Knoten vergleichen und nehmen Sie den Mindestwert an.

2. Vergleichen Sie den kleineren untergeordneten Knoten mit dem übergeordneten Knoten. Wenn der untergeordnete Knoten

3. Wenn der Index des untergeordneten Knotens außerhalb der Grenzen liegt, bedeutet dies, dass er das Ende erreicht hat und beendet ist.

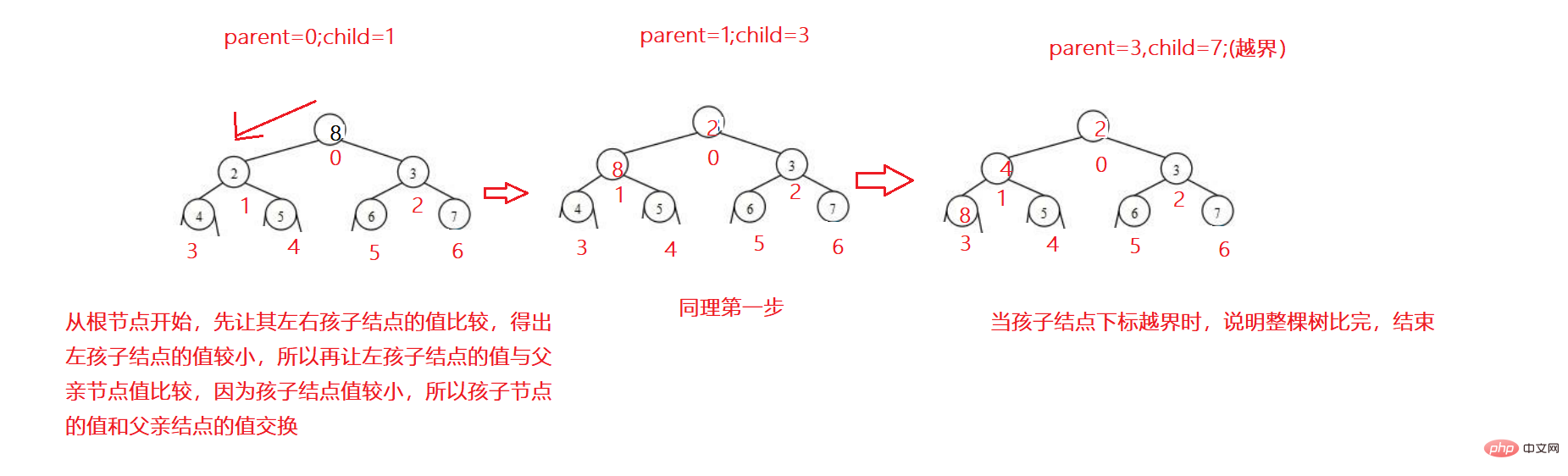
Codebeispiel:

 //parent: 每棵树的根节点
 //len: 每棵树的调整的结束位置
public void shiftDown(int parent,int len){
        int child=parent*2+1; //因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以最起码是有左孩子的，至少有1个孩子
        while(child<len){
            if(child+1<len && elem[child]<elem[child+1]){
                child++;//两孩子结点比较取较小值
            }
            if(elem[child]<elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                parent=child;
                child=parent*2+1;
            }else{
                break;
            }
        }
    }

Aufbau eines Heaps

Angesichts eines Arrays kann dieses Array logischerweise als vollständiger Binärbaum betrachtet werden, es ist jedoch noch kein Heap (der linke und der rechte Teilbaum sind nicht beide groß oder kleiner) Heap), jetzt verwenden wir den Algorithmus, um daraus einen Heap (großer oder kleiner Heap) zu erstellen. Was zu tun? Hier beginnen wir mit der Anpassung vom ersten Teilbaum des letzten Nicht-Blattknotens und passen ihn bis zum Baum des Wurzelknotens an, und dann können wir ihn zu einem Stapel anpassen. Hier verwenden wir die Abwärtsanpassung, die wir gerade geschrieben haben.

public void creatHeap(int[] arr){
        for(int i=0;i<arr.length;i++){
            elem[i]=arr[i];
            useSize++;
        }
        for(int parent=(useSize-1-1)/2;parent>=0;parent--){//数组下标从0开始
            shiftDown(parent,useSize);
        }
    }

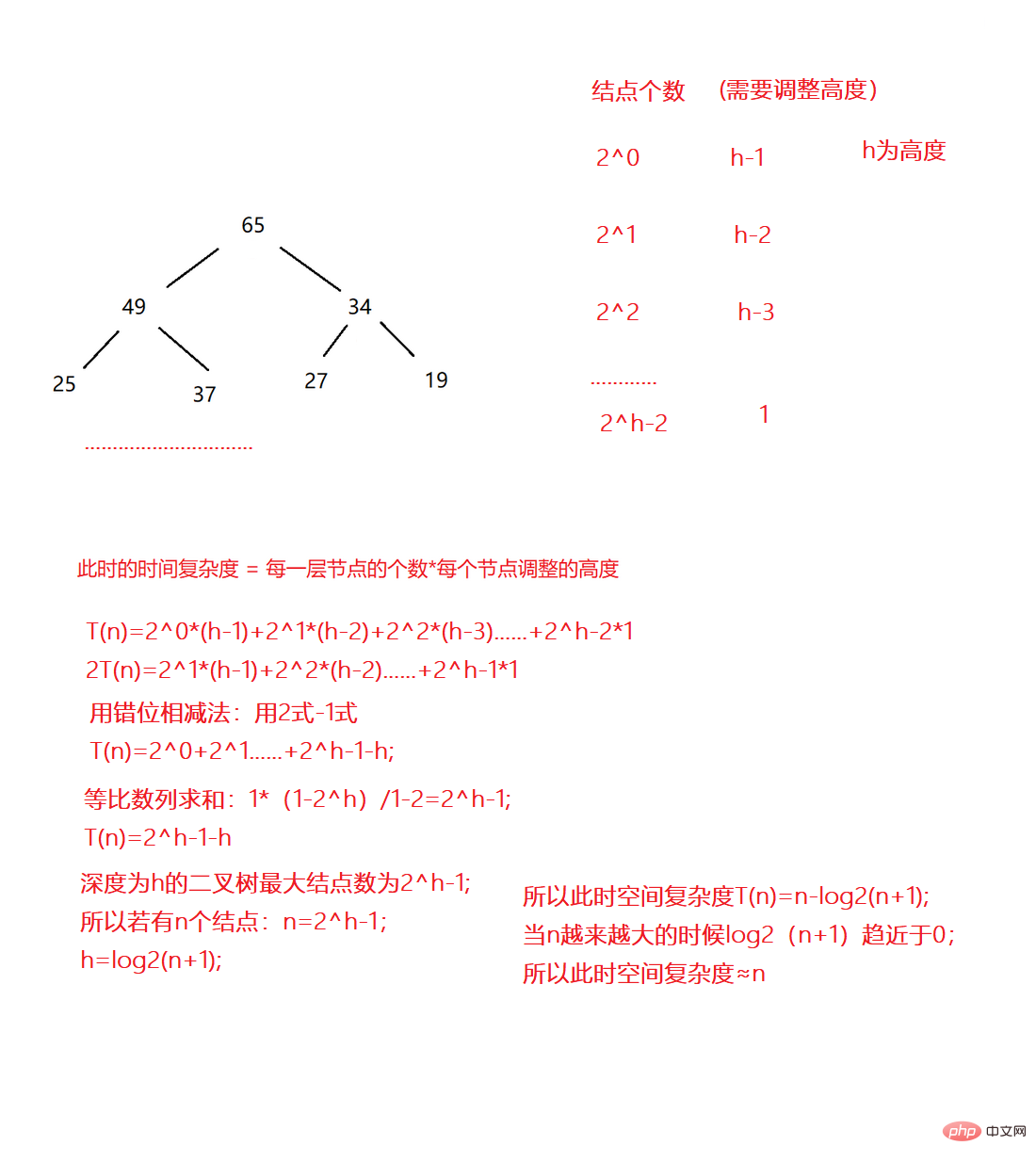
Die räumliche Komplexität beim Aufbau eines Heaps beträgt O(N), da der Heap ein vollständiger Binärbaum ist und ein vollständiger Binärbaum auch ein vollständiger Binärbaum ist (im schlimmsten Fall). beweise es.

Der Heap muss nach oben angepasst werden

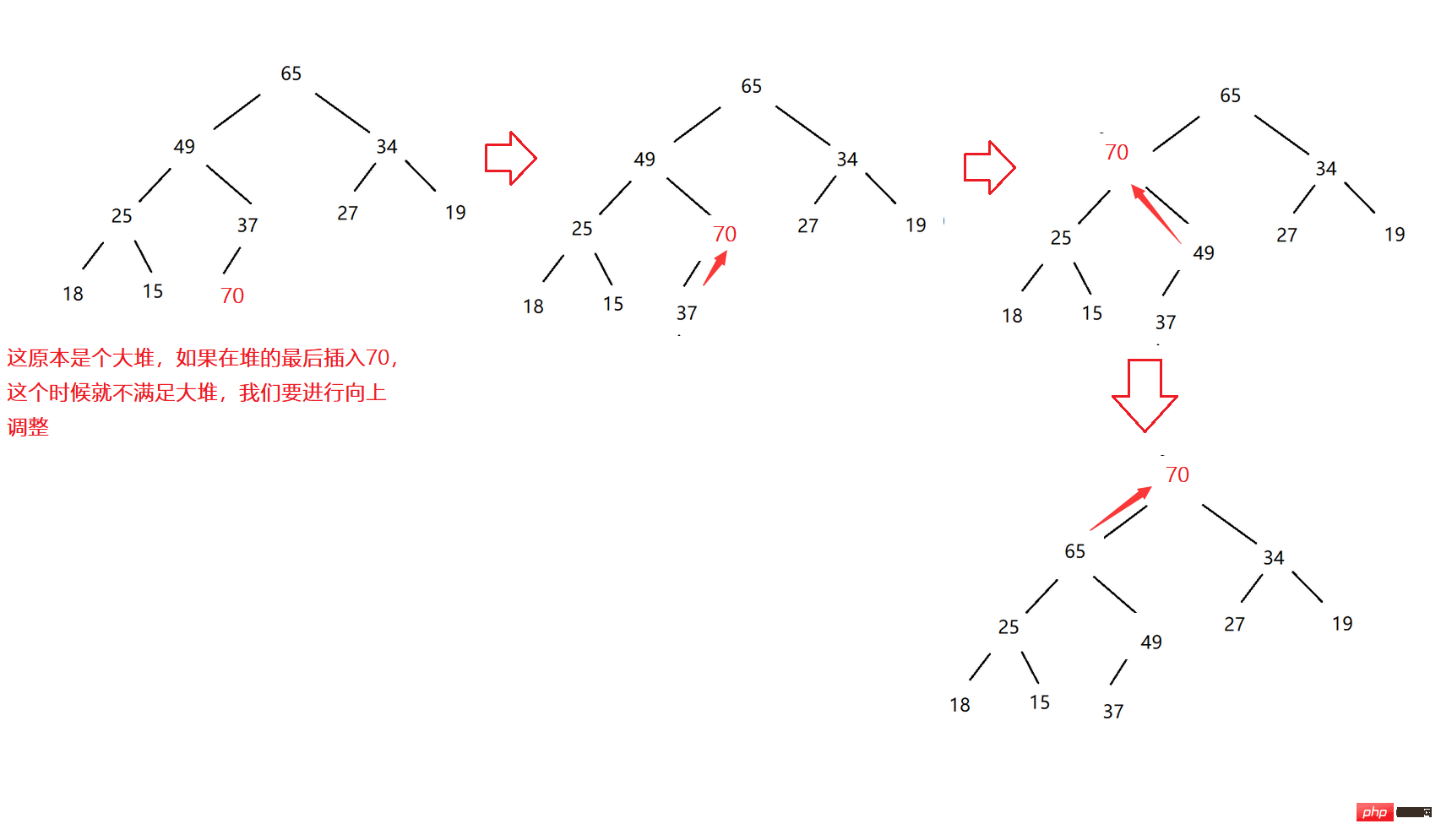
Da es nun einen Heap gibt, müssen wir Daten am Ende des Heaps einfügen und diese dann anpassen, damit die Struktur des Heaps weiterhin erhalten bleibt. Dies ist eine Aufwärtsanpassung.

Nehmen Sie als Beispiel einen großen Heap:

Codebeispiel:

public void shiftup(int child){
        int parent=(child-1)/2;
        while(child>0){
            if(elem[child]>elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

Allgemeine Operationen des Heaps

Enqueue

Fügen Sie Elemente zum Heap hinzu, dh fügen Sie Elemente an der letzten Position hinzu und passen Sie sie dann an nach oben.

public boolean isFull(){
        return elem.length==useSize;
    }
public void offer(int val){
        if(isFull()){
            elem= Arrays.copyOf(elem,2*elem.length);//扩容
        }
        elem[useSize++]=val;
        shiftup(useSize-1);
    }

Dequeue

Um das Element im Heap zu löschen, tauschen Sie das oberste Element des Heaps mit dem letzten Element aus, verringern Sie dann die Größe des gesamten Arrays um eins und passen Sie es schließlich nach unten an, um das oberste Element des Stapels zu löschen .

public boolean isEmpty(){
        return useSize==0;
    }
public int poll(){
        if(isEmpty()){
            throw new RuntimeException("优先级队列为空");
        }
        int tmp=elem[0];
        elem[0]=elem[useSize-1];
        elem[useSize-1]=tmp;
        useSize--;
        shiftDown(0,useSize);
        return tmp;
    }

Holen Sie sich das Teamleiterelement

public int peek() {
        if (isEmpty()) {
            throw new RuntimeException("优先级队列为空");
        }
        return elem[0];
    }

TopK-Frage

Anhand von 6 Daten finden Sie die drei größten Daten. Wie verwenden wir den Heap zu diesem Zeitpunkt?

Ideen zur Problemlösung:

1. Wenn Sie die größten K-Elemente finden möchten, müssen Sie einen kleinen Root-Heap erstellen.

2. Wenn Sie die ersten K kleinsten Elemente finden möchten, müssen Sie einen großen Root-Heap erstellen.

3. Das K-te größte Element. Erstellen Sie einen kleinen Heap, und das oberste Element des Heaps ist das K-te größte Element.

4. Das K-te kleinste Element. Erstellen Sie einen großen Heap, und das oberste Element des Heaps ist das K-te größte Element.

Beispiel

Zum Beispiel: Finden Sie die ersten n größten Daten

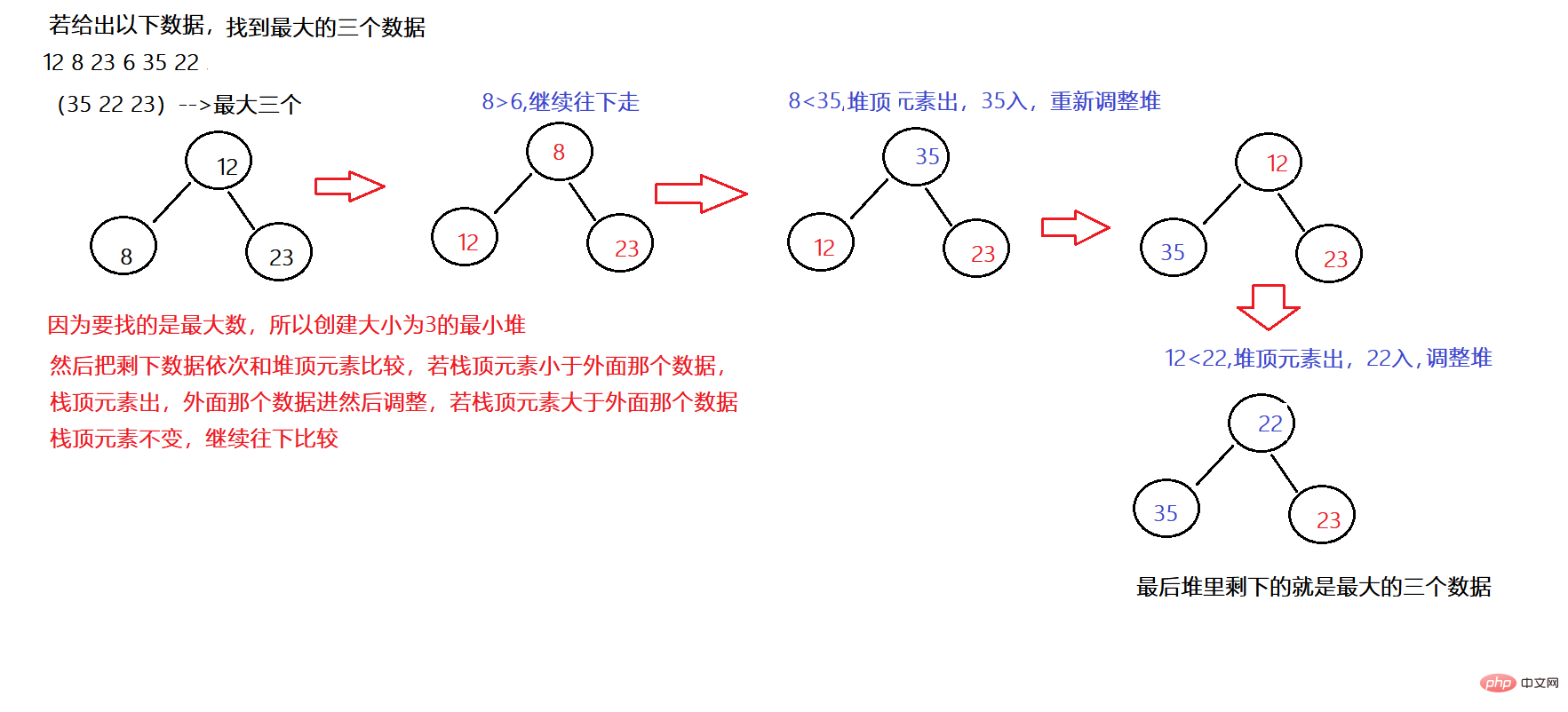
Codebeispiel:

 public static int[] topK(int[] array,int k){
        //创建一个大小为K的小根堆
        PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1-o2;
            }
        });
        //遍历数组中元素，将前k个元素放入队列中
        for(int i=0;i<array.length;i++){
            if(minHeap.size()<k){
                minHeap.offer(array[i]);
            }else{
                //从k+1个元素开始，分别和堆顶元素比较
                int top=minHeap.peek();
                if(array[i]>top){
                    //先弹出后存入
                    minHeap.poll();
                    minHeap.offer(array[i]);
                }
            }
        }
        //将堆中元素放入数组中
        int[] tmp=new int[k];
        for(int i=0;i< tmp.length;i++){
            int top=minHeap.poll();
            tmp[i]=top;
        }
        return tmp;
    }
    public static void main(String[] args) {
        int[] array={12,8,23,6,35,22};
        int[] tmp=topK(array,3);
        System.out.println(Arrays.toString(tmp));
    }

Ergebnis:

Array-Sortierung

Wenn Sie außerdem ein Array von klein nach groß sortieren möchten, Sollten wir große oder kleine Wurzelpfähle verwenden?

---->Dagendui

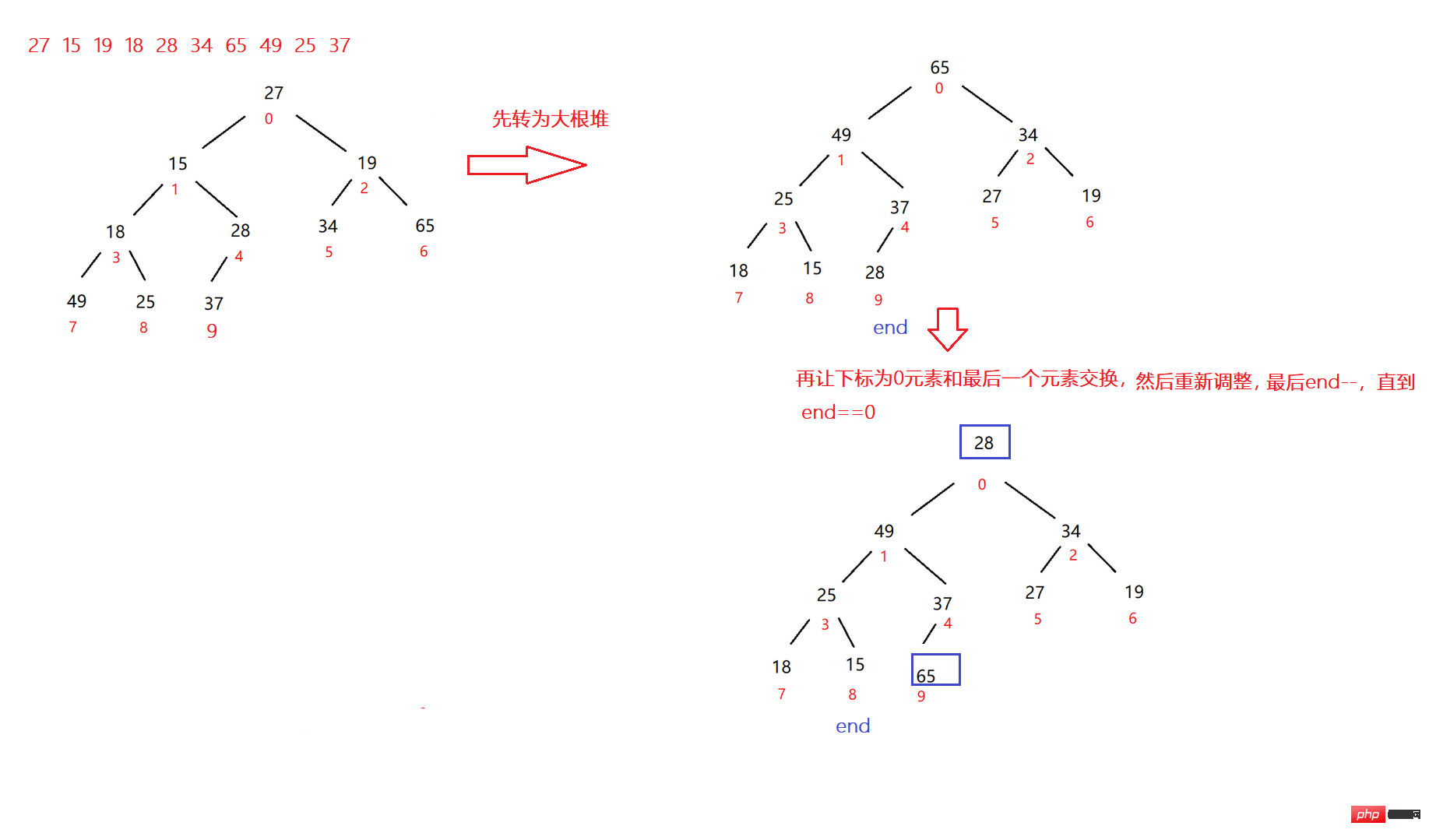
Codebeispiel:

  public void heapSort(){
        int end=useSize-1;
        while(end>0){
            int tmp=elem[0];
            elem[0]=elem[end];
            elem[end]=tmp;
            shiftDown(0,end);//假设这里向下调整为大根堆
            end--;
        }
    }

Das obige ist der detaillierte Inhalt vonSo erstellen Sie einen Heap von Java-Datenstrukturen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!