
Rechenkomplexität ist ein Maß für die Rechenressourcen (Zeit und Raum), die ein bestimmter Algorithmus bei der Ausführung verbraucht.
Rechenkomplexität wird in zwei Kategorien unterteilt:
Zeitkomplexität ist kein Maß für die Leistung eines Algorithmus oder eines Die Zeit, die zum Ausführen auf einer Maschine oder Bedingung benötigt wird. Zeitkomplexität bezieht sich im Allgemeinen auf Zeitkomplexität, eine Funktion, die die Laufzeit des Algorithmus qualitativ beschreibt und es uns ermöglicht, verschiedene Algorithmen zu vergleichen, ohne sie auszuführen. Beispielsweise wird ein Algorithmus mit O(n) immer eine bessere Leistung als O(n²) erbringen, da seine Wachstumsrate geringer als die von O(n²) ist.
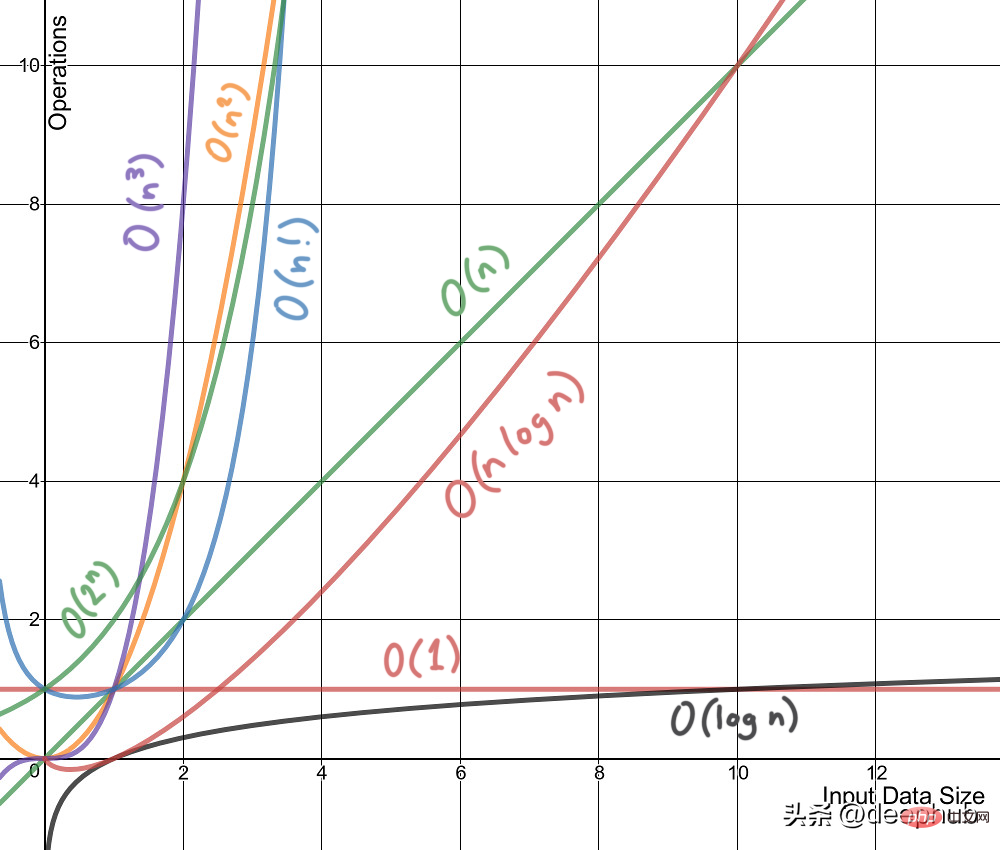
So wie Zeitkomplexität eine Funktion ist, ist auch Raumkomplexität eine Funktion. Vom Konzept her ist es dasselbe wie Zeitkomplexität, ersetzen Sie einfach Zeit durch Raum. Wikipedia definiert Raumkomplexität als:
Die Raumkomplexität eines Algorithmus oder Computerprogramms ist die Menge an Speicherplatz, die erforderlich ist, um eine Instanz eines Rechenproblems als Funktion der Anzahl der eingegebenen Features zu lösen.
Nachfolgend haben wir die Rechenkomplexität einiger gängiger Algorithmen für maschinelles Lernen zusammengestellt.
#🎜🎜 #Laufzeit-Raumkomplexität: O(n*f)
kd-tree:8, K-bedeutet Clustering:
Das obige ist der detaillierte Inhalt vonZusammenfassung der Rechenkomplexität von acht gängigen Algorithmen für maschinelles Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Algorithmus zum Ersetzen von Seiten
Algorithmus zum Ersetzen von Seiten
 So berechnen Sie die Bearbeitungsgebühr für die Rückerstattung der Eisenbahn 12306
So berechnen Sie die Bearbeitungsgebühr für die Rückerstattung der Eisenbahn 12306
 Grafikkarte für Enthusiasten
Grafikkarte für Enthusiasten
 MySQL-Paging-Methode
MySQL-Paging-Methode
 Gängige Tools zum Softwaretesten
Gängige Tools zum Softwaretesten
 Was tun, wenn die chinesische Steckdose verstümmelt ist?
Was tun, wenn die chinesische Steckdose verstümmelt ist?
 MySQL-Platzhalter
MySQL-Platzhalter
 Ist Bitcoin in China legal?
Ist Bitcoin in China legal?




