Um diesen Texttyp zu analysieren, ist eine weitere spezifische Grammatikregel erforderlich. Wir stellen hier die grammatikalischen Regeln Backus-Normalform (BNF) und Erweiterte Backus-Normalform (EBNF) vor, die kontextfreie Grammatik darstellen können. Von so klein wie ein arithmetischer Operationsausdruck bis hin zu so groß wie fast alle Programmiersprachen werden sie mithilfe kontextfreier Grammatiken definiert.
Gehen Sie für einfache arithmetische Operationsausdrücke davon aus, dass wir Wortsegmentierungstechnologie verwendet haben, um sie in einen Eingabe-Token-Stream umzuwandeln, z. B. NUM+NUM*NUM (für Wortsegmentierungsmethoden). , siehe Blogbeitrag zum vorherigen Kapitel). NUM+NUM*NUM（分词方法参见上一篇博文）。
在此基础上，我们定义BNF规则定义如下：
expr ::= expr + term
| expr - term
| term
term ::= term * factor
| term / factor
| factor
factor ::= (expr)
| NUM当然，这种计法还不够简洁明了，我们实际采用的为EBNF形式：
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUMBNF和EBNF每一条规则(形如::=的式子)都可以看做是一种替换，即左侧的符号可以被右侧的符号所替换。我们在解析过程中尝试使用BNF/EBNF将输入文本与语法规则进行匹配，以完成各种替换和扩展。在EBNF中，被放置在{...}*内的规则是可选的，而*则表示可以重复零次或多次（类比于正则表达式）。
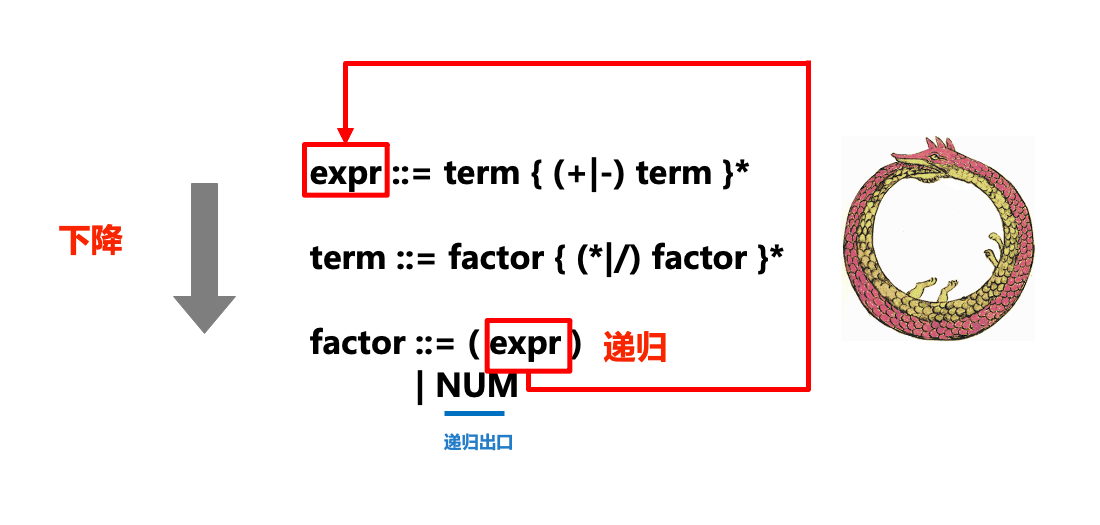
下图形象地展示了递归下降解析器(parser)中“递归”和“下降”部分和ENBF的关系：
在实际的解析过程中，我们对tokens流从左到右进行扫描，在扫描的过程中处理token，如果卡住就产生一个语法错误。每一条语法规则都被转化为一个函数或方法，例如上面的ENBF规则被转换成下述方法：
class ExpressionEvaluator():
...
def expr(self):
...
def term(self):
...
def factor(self):
...在调用某个规则对应方法的过程中，如果我们发现接下来的符号需要采用另一个规则来匹配，则我们就会“下降”到另一个规则方法（如在expr中调用term，term中调用factor），则也就是递归下降中“下降”的部分。
有时也会调用已经在执行的方法（比如在expr中调用term，term中调用factor后，又在factor中调用expr，相当于一条衔尾蛇），这也就是递归下降中“递归”的部分。
对于语法中出现的重复部分（例如expr ::= term { (+|-) term }*），我们则通过while循环来实现。
下面我们来看具体的代码实现。首先是分词部分，我们参照上一篇介绍分词博客的代码。
import re
import collections
# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配数字，+表示任意长度
PLUS = r'(?P<PLUS>\+)' # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意转义
RPAREN = r'(?P<RPAREN>\))' # 注意转义
WS = r'(?P<WS>\s+)' # 别忘记空格，\s表示空格，+表示任意长度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 过滤掉空格符
yield tok下面是表达式求值器的具体实现：
class ExpressionEvaluator():
""" 递归下降的Parser实现，每个语法规则都对应一个方法，
使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
"""
def parse(self, text):
""" 对外调用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一个token，下一个即将匹配的token
self._next() # 转到下一个token
return self.expr() # 开始递归
def _next(self):
""" 转到下一个token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一个token与tok_type匹配，则转到下一个token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 检查是否匹配，如果不匹配则抛出异常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下来是语法规则，每个语法规则对应一个方法
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")我们输入以下表达式进行测试：
e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))求值结果如下：
2
5
14
37
如果我们输入的文本不符合语法规则：
print(e.parse("2 + (3 + * 4)"))则会抛出SyntaxError异常：Expected NUMBER or LPAREN。
综上，可见我们的表达式求值算法运行正确。
上面我们是得到表达式的结果，但是如果我们想分析表达式的结构，生成一棵简单的表达式解析树呢？那么我们需要对上述类的方法做一定修改：
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value) # 字符串转整形
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")输入下列表达式测试一下：
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))以下是生成结果：
('+', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
('+', ('+', 2, 3), 4)
可以看到表达式树生成正确。
我们上面的这个例子非常简单，但递归下降的解析器也可以用来实现相当复杂的解析器，例如Python代码就是通过一个递归下降解析器解析的。您要是对此跟感兴趣可以检查Python源码中的Grammar文件来一探究竟。然而，下面我们接着会看到，自己动手写一个解析器会面对各种陷阱和挑战。
任何涉及左递归形式的语法规则，都没法用递归下降parser来解决。所谓左递归，即规则式子右侧最左边的符号是规则头，比如对于以下规则：
items ::= items ',' item
| item完成该解析你可能会定义以下方法：
def items(self):
itemsval = self.items() # 取第一项，然而此处会无穷递归！
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]这样做会在第一行就无穷地调用self.items()
expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUMJede Regel von BNF und EBNF (ein Ausdruck in der Form ::=) kann als Substitution betrachtet werden, d. h. das Symbol links kann durch das Symbol rechts ersetzt werden . Wir versuchen, BNF/EBNF zu verwenden, um den Eingabetext während des Parsing-Prozesses mit Grammatikregeln abzugleichen, um verschiedene Ersetzungen und Erweiterungen abzuschließen. In EBNF sind in {...}* platzierte Regeln optional und * gibt an, dass sie null oder mehrmals wiederholt werden können (analog zu regulären Ausdrücken).
Die folgende Abbildung zeigt anschaulich die Beziehung zwischen den Teilen „Rekursion“ und „Abstieg“ des rekursiven Abstiegsparsers (Parser) und ENBF:
#🎜🎜#
#🎜🎜##🎜🎜#Im eigentlichen Parsing-Prozess , scannen wir den Tokenstrom von links nach rechts, verarbeiten Token während des Scanvorgangs und generieren einen Syntaxfehler, wenn er hängen bleibt. Jede Grammatikregel wird in eine Funktion oder Methode umgewandelt. Beispielsweise wird die obige ENBF-Regel in die folgende Methode umgewandelt: #🎜🎜#rrreee#🎜🎜#Wenn wir das finden, wird beim Aufrufen der Methode eine entsprechende Regel verwendet Das nächste Das Symbol muss mit einer anderen Regel übereinstimmen, dann werden wir zu einer anderen Regelmethode „absteigen“ (z. B. Term in Ausdruck aufrufen und Faktor in Term aufrufen), was der „absteigende“ Teil des rekursiven Abstiegs ist. #🎜🎜##🎜🎜#Manchmal werden Methoden aufgerufen, die bereits ausgeführt werden (z. B. Term in Ausdruck aufrufen, Faktor in Term aufrufen und dann Ausdruck in Faktor aufrufen, was einem Ouroboros entspricht), was einer Rekursion entspricht „rekursiver“ Teil des Abstiegs. #🎜🎜##🎜🎜#Für die wiederholten Teile, die in der Grammatik vorkommen (z. B. expr ::= term { (+|-) term }*), implementieren wir es durch eine While-Schleife . #🎜🎜##🎜🎜# Schauen wir uns die spezifische Code-Implementierung an. Der erste Teil ist der Wortsegmentierungsteil. Sehen wir uns den vorherigen Artikel an, um den Code des Wortsegmentierungsblogs vorzustellen. #🎜🎜#rrreee#🎜🎜#Das Folgende ist die spezifische Implementierung des Ausdrucksauswerters: #🎜🎜#rrreee#🎜🎜#Wir geben den folgenden Ausdruck zum Testen ein: #🎜🎜#rrreee#🎜🎜#Die Auswertungsergebnisse sind wie folgt:#🎜🎜##🎜🎜#2#🎜🎜#Wenn der von uns eingegebene Text nicht den Anforderungen entspricht mit den grammatikalischen Regeln: #🎜🎜#rrreee#🎜🎜# löst eine SyntaxError-Ausnahme aus:
5
14
37#🎜🎜#
Expected NUMBER or LPAREN. # 🎜🎜#('+', 2, 3)#🎜🎜# Sie können sehen, dass der Ausdruck „Der Baum wurde korrekt generiert“ angezeigt wird. #🎜🎜##🎜🎜# Unser obiges Beispiel ist sehr einfach, aber der rekursive Abstiegsparser kann auch zur Implementierung recht komplexer Parser verwendet werden. Beispielsweise wird Python-Code durch einen rekursiven Abstiegsparser analysiert. Wenn Sie daran interessiert sind, können Sie die Datei
('+', 2, ('*', 3, 4))
('+', 2, ( '*', ( '+', 3, 4), 5))
('+', ('+', 2, 3), 4)#🎜🎜#
Grammar im Python-Quellcode überprüfen, um dies herauszufinden. Wie wir jedoch weiter unten sehen werden, bringt das Schreiben eines Parsers selbst verschiedene Fallstricke und Herausforderungen mit sich. #🎜🎜#self.items() endlos in der ersten Zeile aufgerufen, was zu einem unendlichen Rekursionsfehler führt. #🎜🎜##🎜🎜#Es gibt auch einen Fehler in den Grammatikregeln selbst, beispielsweise in der Operatorpriorität. Wenn wir die Operatorpriorität ignorieren und den Ausdruck direkt wie folgt vereinfachen: #🎜🎜#rrreee#🎜🎜#PYTHON Vollbild kopieren#🎜🎜##🎜🎜#Diese Syntax kann technisch implementiert werden, aber die Berechnungsreihenfolgekonvention wird nicht befolgt, Daraus ergibt sich: Das Ergebnis von „3+4*5“ ist 35 und nicht wie erwartet 23. Daher sind separate Ausdrucks- und Termregeln erforderlich, um die Richtigkeit der Berechnungsergebnisse sicherzustellen. #🎜🎜#Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen rekursiven Abstiegsparser in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
