
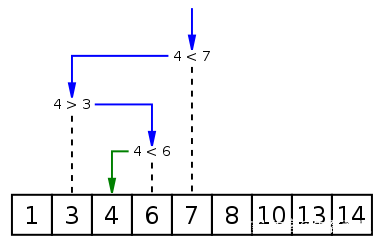
Binäre Suche ist ein Suchalgorithmus zum Suchen eines bestimmten Elements in einem geordneten Array. Der Suchvorgang beginnt beim mittleren Element des Arrays. Wenn das mittlere Element zufällig das zu findende Element ist, endet der Suchvorgang, wenn ein bestimmtes Element größer oder kleiner als das mittlere Element ist die Hälfte des Arrays, die größer oder kleiner als das mittlere Element ist, und starten Sie den Vergleich wie am Anfang vom mittleren Element aus. Wenn das Array in einem bestimmten Schritt leer ist, bedeutet dies, dass es nicht gefunden werden kann. Dieser Suchalgorithmus reduziert den Suchbereich bei jedem Vergleich um die Hälfte.
# 返回 x 在 arr 中的索引,如果不存在返回 -1
def binarySearch (arr, l, r, x):
# 基本判断
if r >= l:
mid = int(l + (r - l)/2)
# 元素整好的中间位置
if arr[mid] == x:
return mid
# 元素小于中间位置的元素,只需要再比较左边的元素
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# 元素大于中间位置的元素,只需要再比较右边的元素
else:
return binarySearch(arr, mid+1, r, x)
else:
# 不存在
return -1
# 测试数组
arr = [ 2, 3, 4, 10, 40]
x = int(input('请输入元素:'))
# 函数调用
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print("元素在数组中的索引为 %d" % result)
else:
print("元素不在数组中")Laufergebnis:
Bitte geben Sie das Element ein: 4
Der Index des Elements im Array ist 2
Bitte geben Sie das Element ein: 5
Das Element ist nicht im Array
Lineare Suche: bezieht sich auf die Überprüfung jedes Elements im Array in einer bestimmten Reihenfolge, bis der spezifische Wert gefunden wird, nach dem Sie suchen.
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i
return -1
# 在数组 arr 中查找字符 D
arr = [ 'A', 'B', 'C', 'D', 'E' ]
x = input("请输入要查找的元素:")
n = len(arr)
result = search(arr, n, x)
if(result == -1):
print("元素不在数组中")
else:
print("元素在数组中的索引为", result)Laufergebnisse:
Bitte geben Sie das gesuchte Element ein: A
Der Index des Elements im Array ist 0
Bitte geben Sie das gesuchte Element ein: a
Das Element ist nicht im Array
Einfügungssortierung: Es ist ein einfacher und intuitiver Sortieralgorithmus. Es funktioniert, indem es eine geordnete Sequenz erstellt. Bei unsortierten Daten scannt es die sortierte Sequenz von hinten nach vorne, findet die entsprechende Position und fügt sie ein.
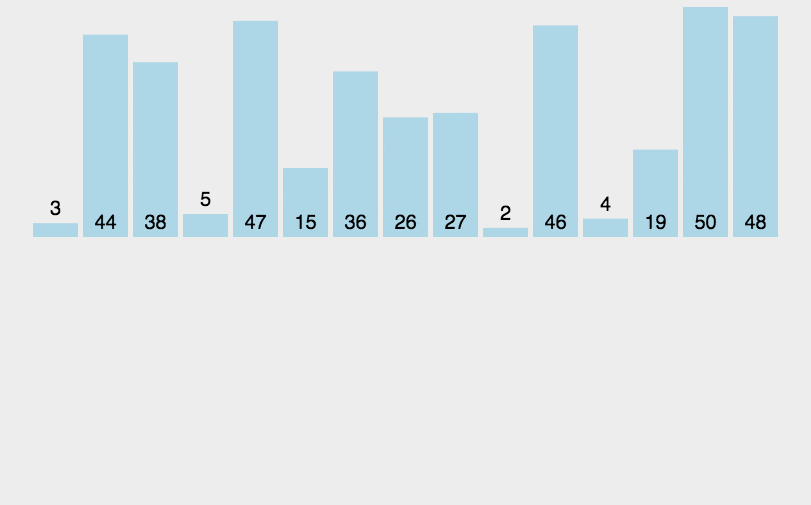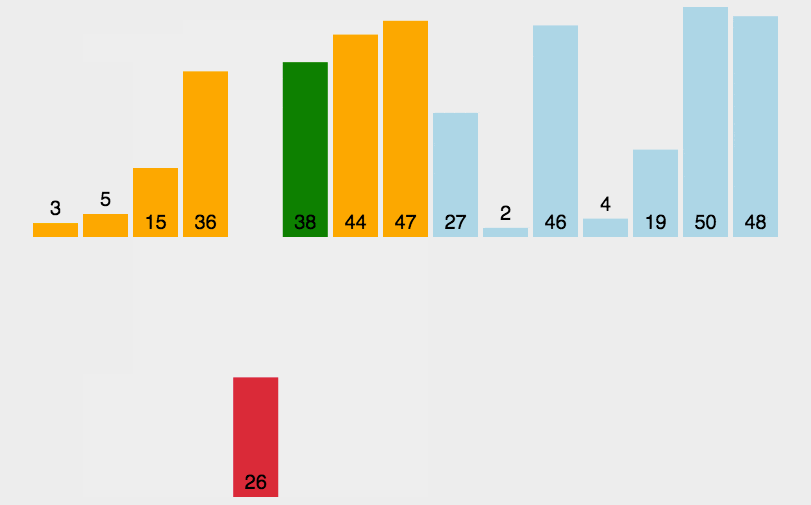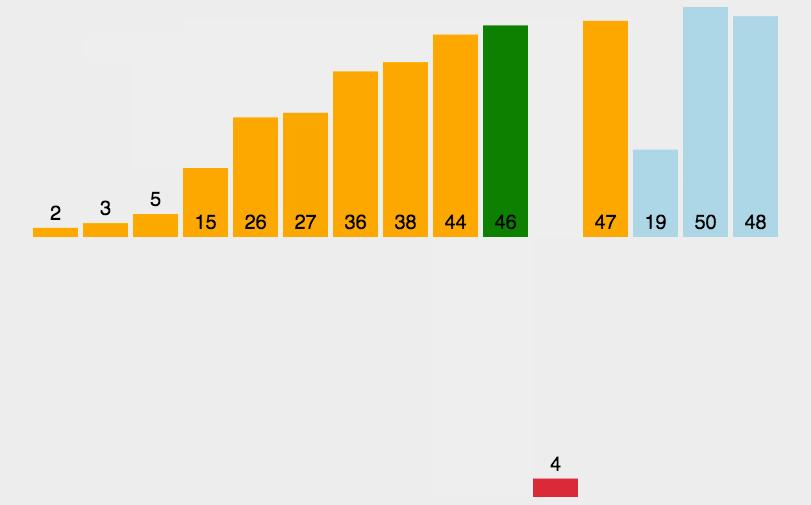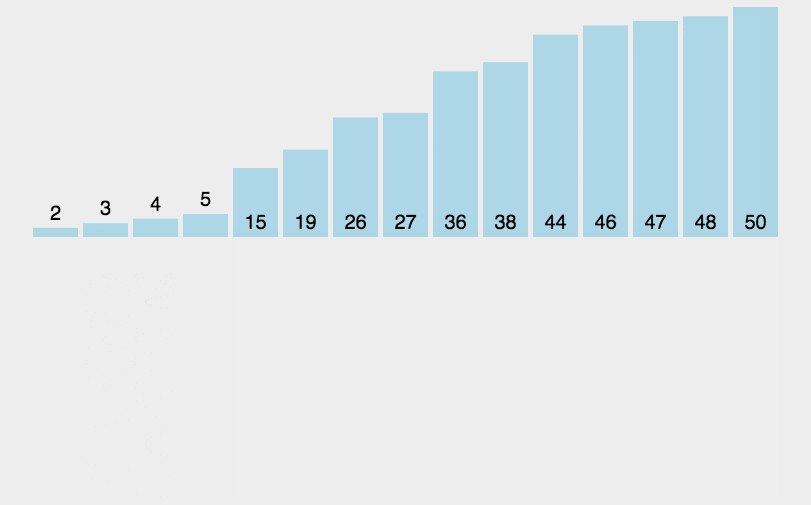
def insertionSort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i-1
while j >= 0 and key < arr[j]:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
arr = [12, 11, 13, 5, 6, 7, 9, 9, 17]
insertionSort(arr)
print("排序后的数组:")
print(arr)Laufendes Ergebnis:
sortiertes Array:
[5, 6, 7, 9, 9, 11, 12, 13, 17]
Natürlich kann es auch so geschrieben werden, was prägnanter ist
list1 = [12, 11, 13, 5, 6, 7, 9, 9, 17]
for i in range(len(list1)-1, 0, -1):
for j in range(0, i):
if list1[i] < list1[j]:
list1[i], list1[j] = list1[j], list1[i]
print(list1)Schnelle Sortierung;Verwenden Sie die Divide-and-Conquer-Strategie, um eine Sequenz (Liste) in zwei Teilsequenzen zu teilen, eine kleinere und eine größere, und sortieren Sie die beiden Teilsequenzen dann rekursiv.
Die Schritte sind:
Wählen Sie den Pivot-Wert aus: Wählen Sie ein Element aus der Sequenz aus, das als „Pivot“ (Pivot) bezeichnet wird Werte sind kleiner als der Pivot-Wert. Kleine Elemente werden vor dem Pivot platziert, und alle Elemente, die größer als der Pivot-Wert sind, werden hinter dem Pivot platziert (Zahlen, die dem Pivot-Wert entsprechen, können auf beide Seiten gehen). Nachdem diese Division abgeschlossen ist, ist die Sortierung des Referenzwerts abgeschlossen.
Rekursive Sortierung der Teilsequenzen: Rekursive Sortierung der Teilsequenzen von Elementen, die kleiner als der Referenzwert sind, und Teilsequenzen von Elementen, die größer als der Referenzwert sind.
Die Beurteilungsbedingung für die Rekursion nach unten ist, dass die Größe der Sequenz Null oder Eins ist. Zu diesem Zeitpunkt ist die Sequenz offensichtlich in Ordnung. Es gibt mehrere spezifische Methoden zur Auswahl des Benchmark-Werts. Diese Auswahlmethode hat einen entscheidenden Einfluss auf die Zeitleistung der Sortierung.
def partition(arr, low, high):
i = (low-1) # 最小元素索引
pivot = arr[high]
for j in range(low, high):
# 当前元素小于或等于 pivot
if arr[j] <= pivot:
i = i+1
arr[i], arr[j] = arr[j], arr[i]
arr[i+1], arr[high] = arr[high], arr[i+1]
return (i+1)
# arr[] --> 排序数组
# low --> 起始索引
# high --> 结束索引
# 快速排序函数
def quickSort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
return arr
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
print("排序后的数组:")
print(quickSort(arr, 0, n-1))Laufergebnisse:
[1, 5, 7, 8, 9, 10]
AuswahlsortierungJa Ein einfaches und intuitiver Sortieralgorithmus . So funktioniert es.
Auswahlsortierung:
A = [64, 25, 12, 22, 11]
for i in range(len(A)):
min_idx = i
for j in range(i+1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
A[i], A[min_idx] = A[min_idx], A[i]
print("排序后的数组:")
print(A)Laufendes Ergebnis:
[11, 12, 22, 25, 64]
Bubble SortAuch A. einfach und intuitiver Sortieralgorithmus. Es durchläuft wiederholt die zu sortierende Sequenz, vergleicht jeweils zwei Elemente und vertauscht sie, wenn sie in der falschen Reihenfolge sind. Der Besuch des Arrays wird wiederholt, bis kein Austausch mehr erforderlich ist, was bedeutet, dass das Array sortiert wurde. Der Name dieses Algorithmus rührt von der Tatsache her, dass kleinere Elemente durch den Austausch langsam an die Spitze des Arrays „schweben“.
Bubble Sort:
def bubbleSort(arr):
n = len(arr)
# 遍历所有数组元素
for i in range(n):
# Last i elements are already in place
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
arr = [64, 34, 25, 12, 22, 11, 90]
print("排序后的数组:")
print(bubbleSort(arr))
[11, 12, 22, 25, 34, 64, 90] 归并排序(Merge sort,或mergesort):,是创建在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 分治法: 分割:递归地把当前序列平均分割成两半。 集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。 运行结果: 给定的数组 堆排序(Heapsort):是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。 运行结果: 排序后的数组 计数排序:的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。 运行结果: 字符数组排序 ccdemnooorwwww 希尔排序:也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。 希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。 运行结果: 排序前: 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。拓扑排序是一种将集合上的偏序转换为全序的操作。 在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序(英语:Topological sorting): 每个顶点出现且只出现一次;若A在序列中排在B的前面,则在图中不存在从B到A的路径。 运行结果: 拓扑排序结果: Das obige ist der detaillierte Inhalt vonBeispielcodeanalyse für den Python-Such- und Sortieralgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!归并排序
def merge(arr, l, m, r):
n1 = m - l + 1
n2 = r - m
# 创建临时数组
L = [0] * (n1)
R = [0] * (n2)
# 拷贝数据到临时数组 arrays L[] 和 R[]
for i in range(0, n1):
L[i] = arr[l + i]
for j in range(0, n2):
R[j] = arr[m + 1 + j]
# 归并临时数组到 arr[l..r]
i = 0 # 初始化第一个子数组的索引
j = 0 # 初始化第二个子数组的索引
k = l # 初始归并子数组的索引
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
# 拷贝 L[] 的保留元素
while i < n1:
arr[k] = L[i]
i += 1
k += 1
# 拷贝 R[] 的保留元素
while j < n2:
arr[k] = R[j]
j += 1
k += 1
def mergeSort(arr, l, r):
if l < r:
m = int((l+(r-1))/2)
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)
return arr
print ("给定的数组")
arr = [12, 11, 13, 5, 6, 7, 13]
print(arr)
n = len(arr)
mergeSort(arr, 0, n-1)
print("排序后的数组")
print(arr)
[12, 11, 13, 5, 6, 7, 13]
排序后的数组
[5, 6, 7, 11, 12, 13, 13]堆排序

def heapify(arr, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # 交换
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n, -1, -1):
heapify(arr, n, i)
# 一个个交换元素
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换
heapify(arr, i, 0)
return arr
arr = [12, 11, 13, 5, 6, 7, 13, 18]
heapSort(arr)
print("排序后的数组")
print(heapSort(arr))
[5, 6, 7, 12, 11, 13, 13, 18]计数排序
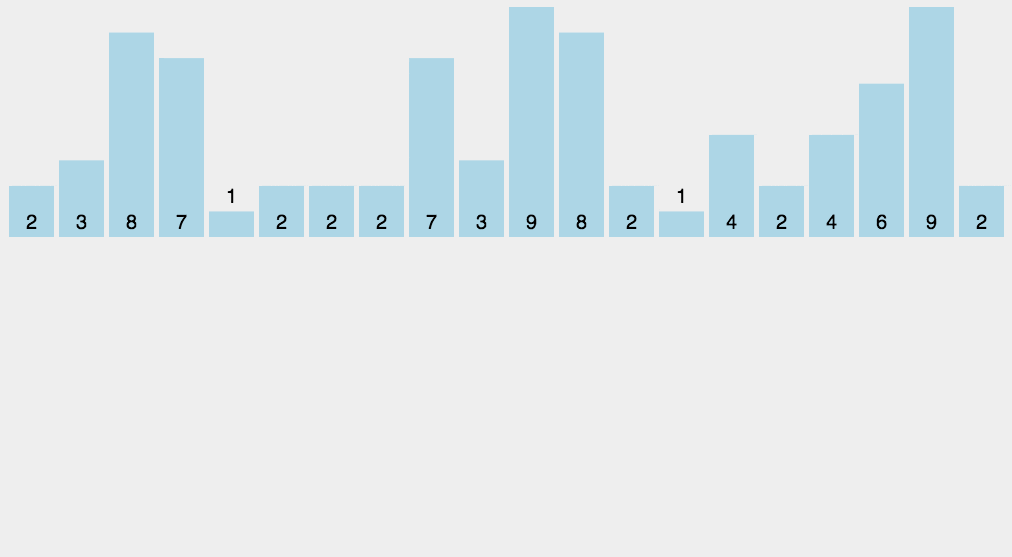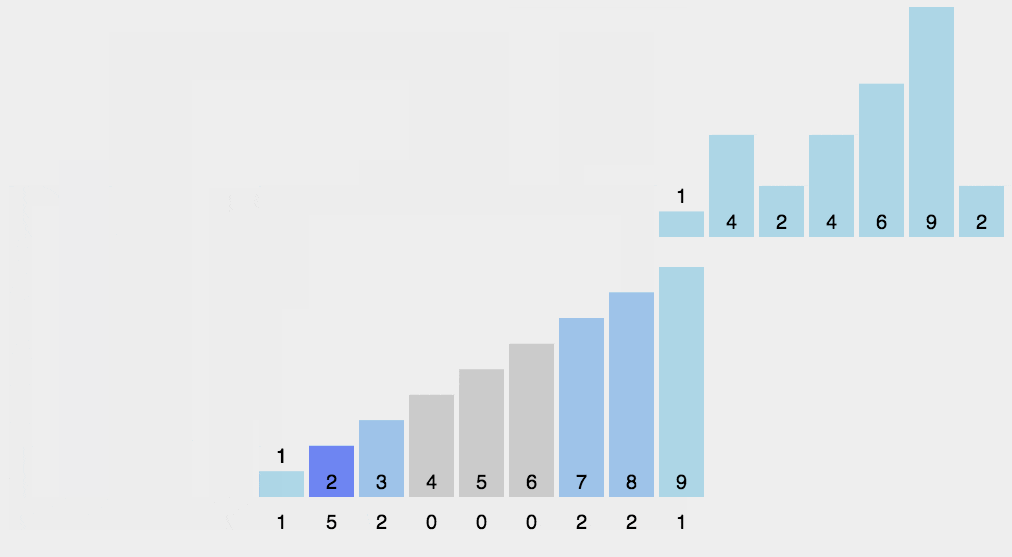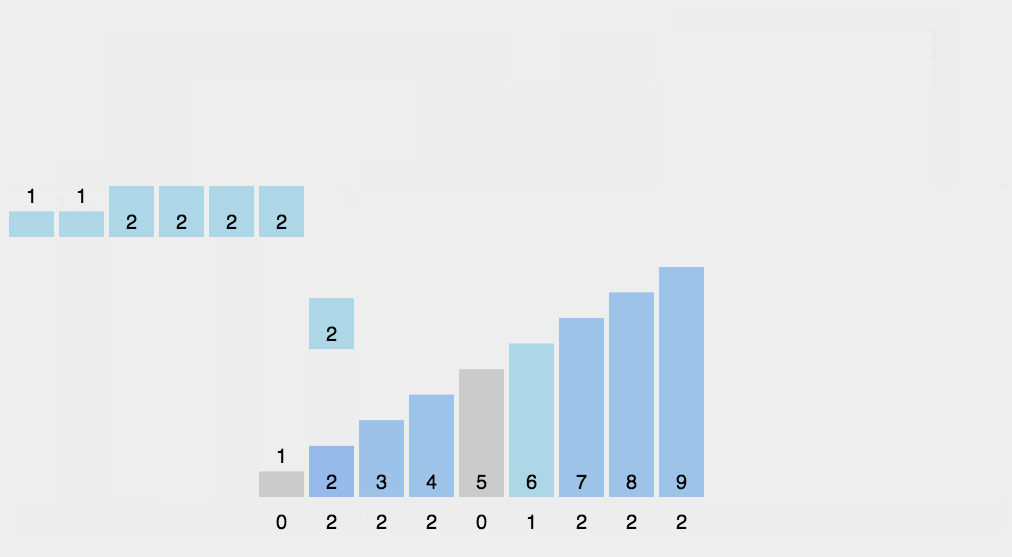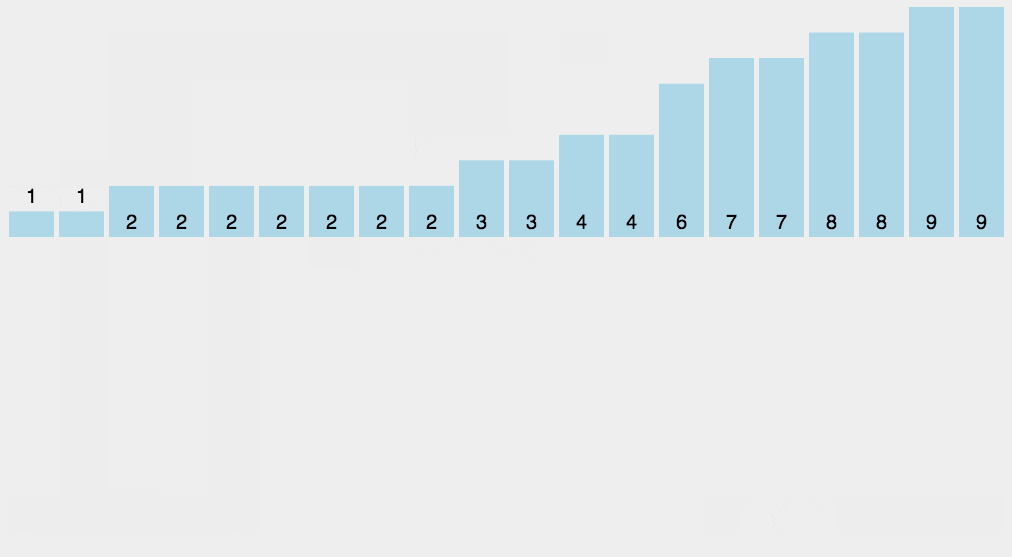
def countSort(arr):
output = [0 for i in range(256)]
count = [0 for i in range(256)]
ans = ["" for _ in arr]
for i in arr:
count[ord(i)] += 1
for i in range(256):
count[i] += count[i-1]
for i in range(len(arr)):
output[count[ord(arr[i])]-1] = arr[i]
count[ord(arr[i])] -= 1
for i in range(len(arr)):
ans[i] = output[i]
return ans
arr = "wwwnowcodercom"
ans = countSort(arr)
print("字符数组排序 %s" %("".join(ans)))希尔排序
def shellSort(arr):
n = len(arr)
gap = int(n/2)
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j-gap] > temp:
arr[j] = arr[j-gap]
j -= gap
arr[j] = temp
gap = int(gap/2)
return arr
arr = [12, 34, 54, 2, 3, 2, 5]
print("排序前:")
print(arr)
print("排序后:")
print(shellSort(arr))
[12, 34, 54, 2, 3, 2, 5]
排序后:
[2, 2, 3, 5, 12, 34, 54]拓扑排序
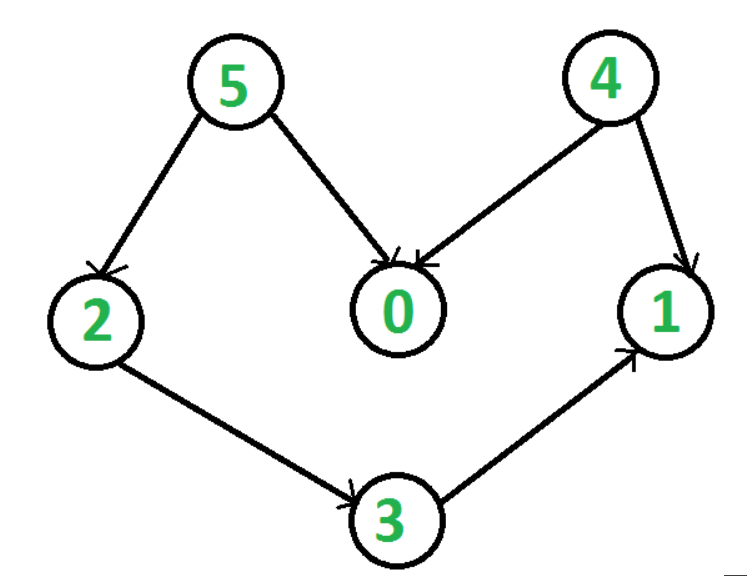
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self, u, v):
self.graph[u].append(v)
def topologicalSortUtil(self, v, visited, stack):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
stack.insert(0,v)
def topologicalSort(self):
visited = [False]*self.V
stack = []
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
print(stack)
g= Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print("拓扑排序结果:")
g.topologicalSort()
[5, 4, 2, 3, 1, 0]




