Durch die Einführung von Caching-Strategien kann Raum in Zeit umgewandelt werden, wodurch die Leistung des Computersystems verbessert wird. Die Rolle des Cachings im Code besteht darin, die Ausführungsgeschwindigkeit des Codes zu optimieren, obwohl dadurch der Speicherbedarf erhöht wird.
In Pythons integrierten Modul-Functools wird die höherwertige Funktion „cache()“ bereitgestellt, um das Caching zu implementieren, das als Dekorator verwendet wird: @cache.
Im Quellcode des Caches lautet die Beschreibung des Caches: Einfacher, leichter, unbegrenzter Cache. Ins Chinesische übersetzt: Einfacher, leichter, unbegrenzter Cache. Manchmal auch „Auswendiglernen“ genannt.
def cache(user_function, /):
'Simple lightweight unbounded cache. Sometimes called "memoize".'
return lru_cache(maxsize=None)(user_function)cache() hat nur eine Codezeile, ruft die Funktion lru_cache() auf und übergibt einen Parameter maxsize=None. lru_cache() ist auch eine Funktion im functools-Modul. Der Standardwert von maxsize ist 128, was bedeutet, dass die Daten 128 überschreiten der LRU-Algorithmus (Longest Unused). Cache() setzt maxsize auf None, dann ist die LRU-Funktion deaktiviert und die Anzahl der Caches kann unendlich wachsen, daher wird dies als „unbegrenzter Cache“ bezeichnet.
lru_cache() verwendet den LRU-Algorithmus (Least Recent Used), der schon lange nicht mehr verwendet wird. Aus diesem Grund enthält der Funktionsname drei Buchstaben lru. Der Mechanismus des am wenigsten verwendeten Algorithmus besteht darin, dass unter der Annahme, dass in der letzten Zeit nicht auf Daten zugegriffen wurde, die Wahrscheinlichkeit, dass auf sie in der Zukunft zugegriffen wird, ebenfalls sehr gering ist. Der LRU-Algorithmus entscheidet sich dafür, die am wenigsten verwendeten Daten zu eliminieren und diejenigen beizubehalten werden häufig verwendet.
cache() ist neu in Python Version 3.9, lru_cache() ist neu in Python 3.2 Version, Cache() hebt die Begrenzung der Anzahl der Caches basierend auf lru_cache() auf und ist tatsächlich mit der Weiterentwicklung der Technologie verbunden Aufgrund der erheblichen Verbesserung der Hardwareleistung handelt es sich bei Cache() und lru_cache() lediglich um unterschiedliche Versionen derselben Funktion.
lru_cache() ist im Wesentlichen ein Dekorator, der eine Cache-Funktion für die Funktion bereitstellt. Er speichert die Maxsize-Gruppe der eingehenden Parameter zwischen und gibt das vorherige Ergebnis direkt zurück, wenn die Funktion das nächste Mal mit denselben Parametern aufgerufen wird, um hohen Overhead oder hohe Kosten zu sparen E/A. Die Aufrufzeit der O-Funktion.
Cache bietet eine Vielzahl von Anwendungsszenarien, z. B. das Zwischenspeichern statischer Webinhalte. Sie können den @cache-Dekorator direkt zur Funktion hinzufügen, mit der Benutzer auf statische Webseiten zugreifen.
In einigen rekursiven Codes wird derselbe Parameter wiederholt übergeben, um den Funktionscode auszuführen. Durch die Verwendung des Caches können wiederholte Berechnungen vermieden und die zeitliche Komplexität des Codes verringert werden.
Als nächstes werde ich die Fibonacci-Folge als Beispiel verwenden, um die Rolle von @cache zu veranschaulichen. Wenn Sie den vorherigen Inhalt noch ein wenig verstehen, werden Sie nach dem Lesen des Beispiels meiner Meinung nach aufgeklärt sein.
Die Fibonacci-Folge bezieht sich auf eine Folge von Zahlen: 1, 1, 2, 3, 5, 8, 13, 21, 34, ..., beginnend mit der dritten Zahl ist jede Zahl die Summe der ersten beiden Zahlen. Die meisten Anfänger haben Code für die Fibonacci-Sequenz geschrieben. Die Implementierung in Python ist sehr prägnant. Wie folgt:
def feibo(n):
# 第0个数和第1个数为1
a, b = 1, 1
for _ in range(n):
# 将b赋值给a,将a+b赋值给b,循环n次
a, b = b, a+b
return aNatürlich gibt es viele Möglichkeiten, den Fibonacci-Sequenzcode zu implementieren (mindestens fünf oder sechs). Um die Anwendungsszenarien von @cache zu veranschaulichen, wird in diesem Artikel eine rekursive Methode zum Schreiben des Codes verwendet Fibonacci-Folge. Wie folgt:
def feibo_recur(n):
if n < 0:
return "n小于0无意义"
# n为0或1时返回1（前两个数为1）
if n == 0 or n == 1:
return 1
# 根据斐波那契数列的定义，其他情况递归返回前两个数之和
return feibo_recur(n-1) + feibo_recur(n-2)Wenn der rekursive Code ausgeführt wird, rekursiert er bis zu feibo_recur(1) und feibo_recur(0), wie in der Abbildung unten gezeigt (am Beispiel der sechsten Zahl).
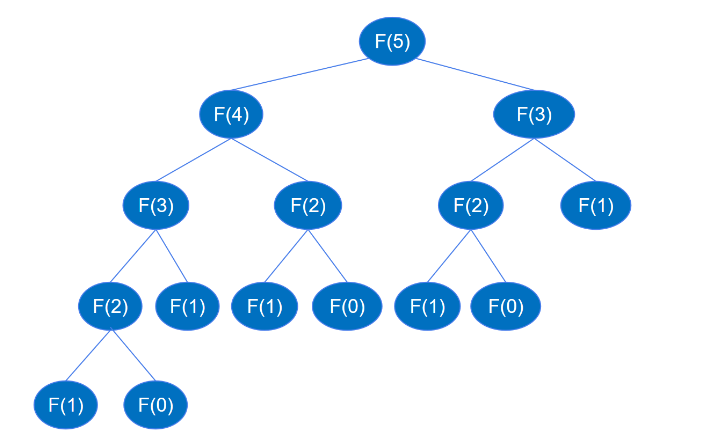
Wenn Sie F(5) finden, müssen Sie zuerst F(4) und F(3) finden, und wenn Sie F(4) finden, müssen Sie zuerst F(3) und F(2) finden.. . und so weiter, rekursiv Der Prozess ähnelt dem Prozess der Tiefendurchquerung eines Binärbaums. Es ist bekannt, dass ein Binärbaum mit der Höhe k bis zu 2k-1 Knoten haben kann. Gemäß dem obigen rekursiven Aufrufdiagramm beträgt die Höhe des Binärbaums höchstens 2n-1 Die Anzahl der rekursiven Funktionsaufrufe beträgt höchstens 2n-1, sodass die Zeitkomplexität der Rekursion O(2^n) beträgt.
Wenn die Zeitkomplexität O(2^n) ist, ändert sich die Ausführungszeit sehr stark, wenn n zunimmt. Testen wir es in der Praxis.
import time
for i in [10, 20, 30, 40]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)Ausgabe:
Die 10. Fibonacci-Zahl: 89
n=10 Kostenzeit: 0,0
Die 20. Fibonacci-Zahl: 10946
n=20 Kostenzeit: 0,0015988349914550781
Der 30. Fibonacci Zahl Bonacci-Zahl: 1346269
n=30 Kostenzeit: 0,17051291465759277
Die 40. Fibonacci-Zahl: 165580141
n=40 Kostenzeit: 20,90010976791382
Aus der Laufzeit ist ersichtlich, dass, wenn n sehr lang ist, die Laufzeit sehr gut zunimmt Besonders wenn n allmählich auf 30 und 40 ansteigt, ändert sich die Laufzeit besonders deutlich. Um das Zeitumstellungsmuster klarer zu erkennen, wurden weitere Tests durchgeführt.
for i in [41, 42, 43]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)Ausgabe:
Die 41. Fibonacci-Zahl: 267914296
n=41 Kostenzeit: 33,77224683761597
Die 42. Fibonacci-Zahl: 433494437
n=42 Kostenzeit: 55,863986 96899414
Die 43. Fidschi-Bonacci-Zahl: 701408733
n=43 Kostenzeit: 92.55108690261841
从上面的变化可以看到，时间是指数级增长的（大约按1.65的指数增长），这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度，假如要计算第50个斐波那契数列，差不多要等一个小时，非常不合理，也说明递归的实现方式运算量过大，存在明显的不足。如何解决这种不足，降低运算量呢？接下来看如何进行优化。
根据前面的分析，递归代码运算量大，是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2)，如示例图中，要得到 feibo_recur(5) ，feibo_recur(1) 调用了5次。随着 n 的增大，调用次数呈指数级增长，导致出现大量的重复操作，浪费了许多时间。
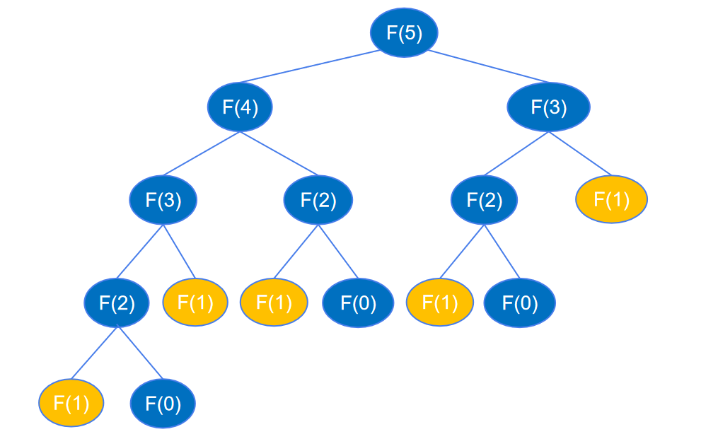
假如有一个地方将每个 n 的执行结果记录下来，当作“备忘录”，下次函数再接收到这个相同的参数时，直接从备忘录中获取结果，而不用去执行递归的过程，就可以避免这些重复调用。在 Python 中，可以创建一个字典或列表来当作“备忘录”使用。
temp = {} # 创建一个空字典，用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
if n < 0:
return "n小于0无意义"
# n为0或1时返回1（前两个数为1）
if n == 0 or n == 1:
return 1
if n in temp: # 如果temp字典中有n,则直接返回值,不调用递归代码
return temp[n]
else:
# 如果字典中还没有第n个斐波那契数，则递归计算并保存到字典中
temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
return temp[n]上面的代码中，创建了一个空字典用于存放每个 n 的执行结果。每次调用函数，都先查看字典中是否有记录，如果有记录就直接返回，没有记录就递归执行并将结果记录到字典中，再从字典中返回结果。这里的递归其实都只执行了一次计算，并没有真正的递归，如第一次传入 n 等于 5，执行 feibo_recur_temp(5)，会递归执行 n 等于 4, 3, 2, 1, 0 的情况，每个 n 计算过一次后 temp 中都有了记录，后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加，执行一次计算，所以时间复杂度是 O(n) 。
下面看一下代码的运行时间。
for i in [10, 20, 30, 40, 41, 42, 43]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)
print(temp)Output:
第10个斐波那契数: 89
n=10 Cost Time: 0.0
第20个斐波那契数: 10946
n=20 Cost Time: 0.0
第30个斐波那契数: 1346269
n=30 Cost Time: 0.0
第40个斐波那契数: 165580141
n=40 Cost Time: 0.0
第41个斐波那契数: 267914296
n=41 Cost Time: 0.0
第42个斐波那契数: 433494437
n=42 Cost Time: 0.0
第43个斐波那契数: 701408733
n=43 Cost Time: 0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}
可以观察到，代码的运行时间已经减少到小数点后很多位了（时间过短，只显示了0.0）。然而，temp 字典存储了每个数字的斐波那契数，这需要使用额外的内存空间，以换取更高的时间效率。
上面的代码也可以用列表来当“备忘录”，代码如下。
temp = [1, 1]
def feibo_recur_temp(n):
if n < 0:
return "n小于0无意义"
if n == 0 or n == 1:
return 1
if n < len(temp):
return temp[n]
else:
# 第一次执行时，将结果保存到列表中，后续直接从列表中取
temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
return temp[n]现在，已经剖析了递归代码重复执行带来的时间复杂度问题，也给出了优化时间复杂度的方法，让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存，在下次以相同参数调用函数时直接返回上一次的结果，与上面的优化方式完全一致。
所以，只需要在递归函数上加 @cache 装饰器，递归的重复执行就可以解决，时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下：
from functools import cache
@cache
def feibo_recur(n):
if n < 0:
return "n小于0无意义"
if n == 0 or n == 1:
return 1
return feibo_recur(n-1) + feibo_recur(n-2)使用 @cache 装饰器，可以让代码更简洁优雅，并且让你专注于处理业务逻辑，而不需要自己实现缓存。下面看一下实际的运行时间。
for i in [10, 20, 30, 40, 41, 42, 43]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)Output:
第10个斐波那契数: 89
n=10 Cost Time: 0.0
第20个斐波那契数: 10946
n=20 Cost Time: 0.0
第30个斐波那契数: 1346269
n=30 Cost Time: 0.0
第40个斐波那契数: 165580141
n=40 Cost Time: 0.0
第41个斐波那契数: 267914296
n=41 Cost Time: 0.0
第42个斐波那契数: 433494437
n=42 Cost Time: 0.0
第43个斐波那契数: 701408733
n=43 Cost Time: 0.0
完美地解决了问题，所有运行时间都被精确到了小数点后数位（即使只显示 0.0），非常巧妙。若今后遇到类似情形，可以直接采用 @cache 实现缓存功能，通过“记忆化”处理。
@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果，以便遇到相同参数可以直接给出答案。前者无限制存储数量，而后者通过设定maxsize限制存储数量的上限。
例：
@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
print('开始计算a+b的值...')
return a + b可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果，都需要额外的空间。不过用装饰器可以省略额外空间代码，减少了出错的风险。
Das obige ist der detaillierte Inhalt vonSo verwenden Sie @cache in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
