
In diesem Abschnitt stellen wir Algorithmen vor, die sich auf gerichtete Diagramme beziehen. Daher werden wir zunächst einige Konzepte gerichteter Diagramme erläutern. In den folgenden Artikeln werden diese Konzepte nicht im Detail erläutert. Zunächst werden die Knoten des gerichteten Graphen durch Linien mit Pfeilen verbunden. Der Out-Grad und der In-Grad eines Knotens können verwendet werden, um ihn zu beschreiben. Wenn das Ende einer Verbindung auf den Knoten zeigt, erhöht sich sein Out-Grad, und wenn der Pfeil einer Verbindung auf den Knoten zeigt, erhöht sich sein Out-Grad. sein In-Grad erhöht sich um 1. Schauen Sie sich das folgende Beispiel an: A hat einen In-Grad von 0 und einen Out-Grad von 2, B hat einen In-Grad von 1 und einen Out-Grad von 1, C hat einen In-Grad von 1 und einen Out-Grad D hat einen Ein-Grad von 1, D einen Ein-Grad von 2 und einen Aus-Grad von 0.
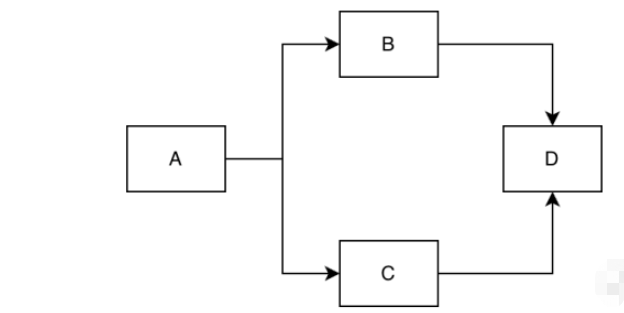
Adjazenzliste: Die Adjazenzliste ist eine effektive Möglichkeit, die Diagrammstruktur zu speichern. Wie in der Abbildung unten gezeigt, speichert das Knotenarray auf der linken Seite alle Knoten im Diagramm und die Adjazenzliste auf der rechten Seite die benachbarten Knoten des Knotens.
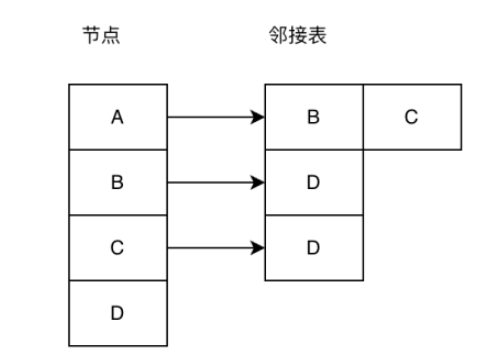
In diesem Artikel werden wir über die topologische Sortierung sprechen, einen Algorithmus für gerichtete azyklische Graphen. Er wird hauptsächlich zur Lösung der Beziehung zwischen Vorgänger und Nachfolger verwendet, dh wenn wir den Strom vervollständigen Welche Aufgabe müssen wir zuerst erledigen? Tatsächlich wird dies häufig in unserer Prozesssteuerung verwendet. Wenn wir uns das Bild unten ansehen, müssen wir zuerst Punkt A abschließen und dann können wir die Punkte B und C abschließen. Die Punkte B und C sind parallel und nicht in der richtigen Reihenfolge, aber Punkt D kann erst abgeschlossen werden, nachdem die Punkte B und C abgeschlossen sind. Die topologische Sortierung kann uns dabei helfen, eine angemessene Reihenfolge für die Vervollständigung von Elementen zu finden. Schauen wir uns gleichzeitig das obige Beispiel an. Nachdem Element A abgeschlossen ist, sind die Elemente B und C nicht in der richtigen Reihenfolge erfüllt sind, daher ist die Reihenfolge der topologischen Sortierung nicht völlig sicher.
Zunächst entspricht die topologische Sortierung einem gerichteten azyklischen Graphen. Für einen azyklischen Graphen muss es mindestens einen Knoten mit Ingrad 0 geben. In der aktuellen Situation müssen wir einen Knoten mit einem In-Grad von 0 für den Betrieb finden. Ein In-Grad von 0 bedeutet, dass der aktuelle Knoten keinen Vorgängerknoten hat oder der Vorgängerknoten verarbeitet wurde und direkt betrieben werden kann. Nachdem die Operation abgeschlossen ist, werden alle In-Grade der Nachfolgerknoten des aktuellen Knotens um 1 reduziert und der Knoten mit einem In-Grad-Knoten von 0 wird erneut nach der Operation durchsucht. Danach handelt es sich um einen rekursiven Prozess Knoten mit einem In-Grad von 0 werden in der aktuellen Situation kontinuierlich verarbeitet, bis alle Knoten vollständig verarbeitet sind.
Das Folgende ist die Struktur eines gerichteten Diagramms, wobei node alle Knoten im aktuellen Diagramm speichert und adj die benachbarten Punkte speichert, die den indizierten Knoten entsprechen. Beim Initialisieren des Diagramms müssen Sie die Anzahl der Knoten angeben und ein Knotenarray und ein Adjazenzarray erstellen. Stellt eine Methode namens addEdge bereit, mit der eine Kante zwischen zwei Knoten erstellt wird, d. h. der Nachfolgerknoten zur Adjazenzliste des Vorgängerknotens hinzugefügt wird.
public static class Graph{
/**
* 节点个数
*/
private Integer nodeSize;
/**
* 节点
*/
private char[] node;
/**
* 邻接表
*/
private LinkedList[] adj;
public Graph(char[] node) {
this.nodeSize = node.length;
this.node = node;
this.adj = new LinkedList[nodeSize];
for (int i = 0 ; i < adj.length ; i++) {
adj[i] = new LinkedList();
}
}
/**
* 在节点之间加边,前驱节点指向后继节点
* @param front 前驱节点所在下标
* @param end 后继节点所在下标
*/
public void addEdge(int front, int end) {
adj[front].add(end);
}
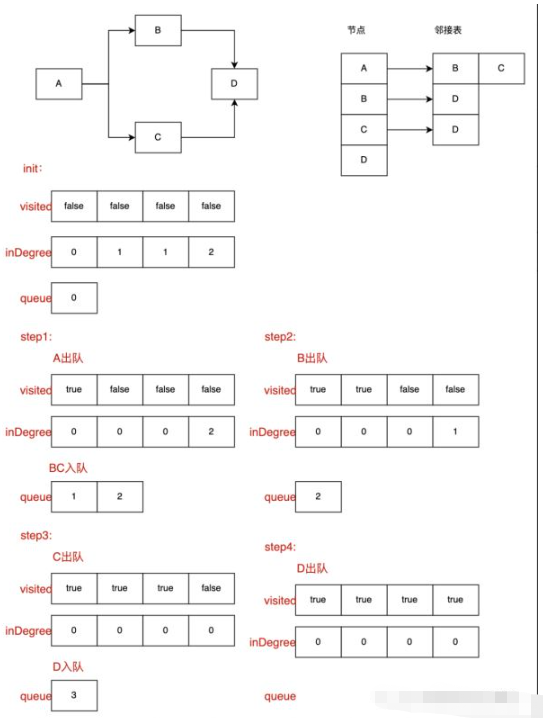
}Die topologische Sortierung initialisiert zunächst zwei temporäre Arrays, eine Warteschlange und ein inDegree-Array, um den In-Grad des entsprechenden Indexknotens zu speichern, da jeder Knoten, auf den zugegriffen wird, erfordert, dass der Vorgängerknoten abgeschlossen wurde, d. h. der In-Grad ist 0. Mit diesem Array können wir diese Knoten relativ schnell finden; das andere ist das besuchte Array, das markiert, ob der aktuelle Knoten besucht wurde, um mehrere Besuche zu verhindern; Grad von 0 in der aktuellen Situation. (Beachten Sie, dass wir alle zur Vereinfachung des Zugriffs Knotenindizes speichern. Schritt 1: Initialisieren Sie das inDegree-Array und das besuchte Array. Schritt 2: Durchlaufen Sie das inDegree-Array und stellen Sie alle Knoten mit einem Indegree von 0 in die Knotenwarteschlange. Schritt 3: Verlassen Sie den Knoten Knoten nacheinander. Bestimmen Sie, ob der aktuelle Knoten besucht wurde. Wenn ja, kehren Sie zu Schritt 3 zurück. Wenn nicht, fahren Sie mit dem nächsten Schritt fort Bestimmen Sie, ob der In-Grad des benachbarten Knotens 0 ist. Wenn er 0 ist, stellen Sie ihn direkt in die Knotenwarteschlange. Wenn er nicht 0 ist, kehren Sie zu Schritt 3 zurück
Testprobe 2
/**
* @param graph 有向无环图
* @return 拓扑排序结果
*/
public List<Character> toPoLogicalSort(Graph graph) {
//用一个数组标志所有节点入度
int[] inDegree = new int[graph.nodeSize];
for (LinkedList list : graph.adj) {
for (Object index : list) {
++ inDegree[(int)index];
}
}
//用一个数组标志所有节点是否已经被访问
boolean[] visited = new boolean[graph.nodeSize];
//开始进行遍历
Deque<Integer> nodes = new LinkedList<>();
//将入度为0节点入队
for (int i = 0 ; i < graph.nodeSize; i++) {
if (inDegree[i] == 0) {
nodes.offer(i);
}
}
List<Character> result = new ArrayList<>();
//将入度为0节点一次出队处理
while (!nodes.isEmpty()) {
int node = nodes.poll();
if (visited[node]) {
continue;
}
visited[node] = true;
result.add(graph.node[node]);
//将当前node的邻接节点入度-1;
for (Object list : graph.adj[node]) {
-- inDegree[(int)list];
if (inDegree[(int)list] == 0) {
//前驱节点全部访问完毕,入度为0
nodes.offer((int) list);
}
}
}
return result;
}Ausführungsergebnis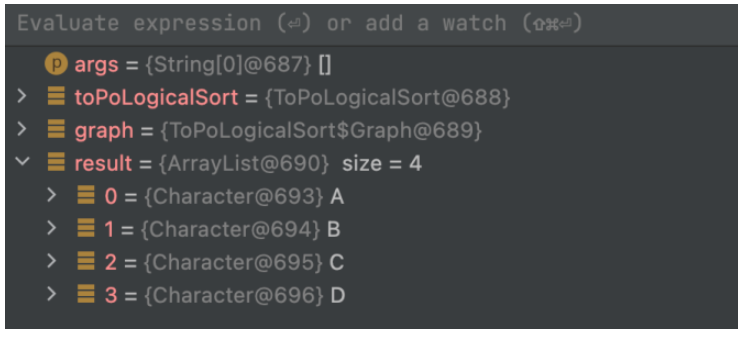
Das obige ist der detaillierte Inhalt vonSo implementieren Sie die topologische Sortierung in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




