Was ist der Unterschied zwischen B-Tree-Index und B+-Tree-Index in MySQL?

Wenn Sie einen Baum als Indexdatenstruktur verwenden, wird bei jeder Datensuche ein Knoten des Baums von der Festplatte gelesen, bei dem es sich um eine Seite handelt. Allerdings speichert jeder Knoten des Binärbaums nur ein Datenelement , der nicht eine Seite Speicherplatz füllen kann, wäre der zusätzliche Speicherplatz nicht verschwendet? Um dieses Manko des binär ausgeglichenen Suchbaums zu beheben, sollten wir nach einer Datenstruktur suchen, die mehr Daten in einem einzelnen Knoten speichern kann, also einem Mehrweg-Suchbaum.

1. Mehrweg-Suchbaum

1. Vollständige Binärbaumhöhe: O(log2N), wobei 2 der Logarithmus ist, die Anzahl der Knoten auf jeder Ebene des Baumes O(log2N)，其中2为对数，树每层的节点数；

2、完全M路搜索树的高度：O(logmN)，其中M为对数，树每层的节点数；

M路搜索树适用于存储数据量过大无法一次性加载到内存的场景。通过增加每层节点的个数和在每个节点存放更多的数据来在一层中存放更多的数据，从而降低树的高度，在数据查找时减少磁盘访问次数。

因此，如果每个节点包含的关键字数量和每层的节点数量增加，则树的高度将减少。尽管每个节点的数据确定会更加耗时，但B树的关注点在于解决磁盘性能瓶颈，因此单个节点搜索数据的成本可以被忽略。

2. B树-多路平衡搜索树

B树是一种M路搜索树，B树主要用于解决M路搜索树的不平衡导致树的高度变高，跟二叉树退化为链表导致性能问题一样。B树通过对每层的节点进行控制、调整，如节点分离，节点合并，一层满时向上分裂父节点来增加新的层等操作来来保证该M路搜索树的平衡。

在B树中，每个节点都是一个磁盘块（页），而阶数或者说路数M则规定了节点中最多的子节点数量。每个非叶子节点存放了关键字和指向儿子树的指针，具体数量为：M阶的B树，每个非叶子节点存放了M-1个关键字和M个指向子树的指针。如图为5阶B树结构的示意图：

3. B树索引

首先创建一张user表：

create table user(
	id int,
	name varchar,
	primary key(id)
) ROW_FORMAT=COMPACT;

假如我们使用B树对表中的用户记录建立索引：

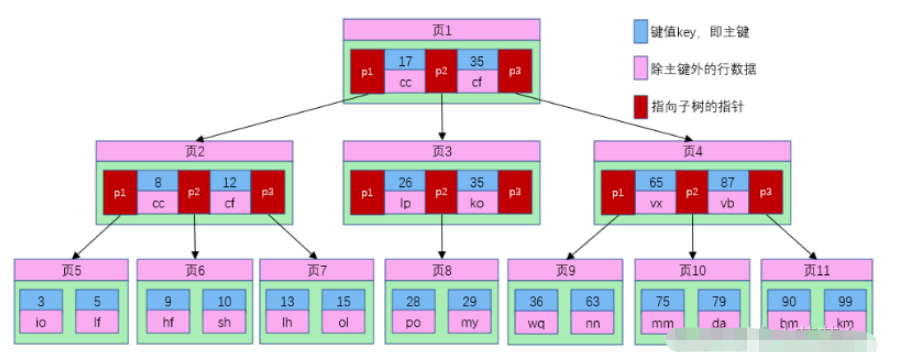
B树的每个节点占用一个磁盘块，磁盘块也就是页，从上图可以看出，B树相对于平衡二叉树，每个节点存储了更多的主键key和数据data，并且每个节点拥有了更多的子节点，子节点的个数一般称为阶，上述图中的B树为3阶B树，高度也会降低。假如我们要查找id=28的用户信息，那么查找流程如下：

1、根据根节点找到页1，读入内存。【磁盘I/O操作第1次】

2、比较键值28在区间（17,35），找到页1的指针p2；

3、根据p2指针找到页3，读入内存。【磁盘I/O操作第2次】

4、比较键值28在区间（26,35），找到页3的指针p2。

5、根据p2指针找到页8，读入内存。【磁盘I/O操作第3次】

6、在页8中的键值列表中找到键值28，键值对应的用户信息为(28,po)；

B-Tree相对于AVLTree

2 . Vollständiger M-Wege-Suchbaum. Die Höhe: O(logmN), wobei M der Logarithmus ist, die Anzahl der Knoten in jeder Ebene des Baums.

M-Wege-Suchbaum ist für Szenarien geeignet wo die Menge der gespeicherten Daten zu groß ist, um sie auf einmal in den Speicher zu laden. Speichern Sie mehr Daten in einer Schicht, indem Sie die Anzahl der Knoten pro Schicht erhöhen und mehr Daten in jedem Knoten speichern. Dadurch wird die Höhe des Baums verringert und die Anzahl der Festplattenzugriffe während der Datensuche verringert.

Wenn also die Anzahl der Schlüsselwörter, die jeder Knoten enthält, und die Anzahl der Knoten pro Ebene zunimmt, verringert sich die Höhe des Baums. Obwohl die Datenermittlung jedes Knotens zeitaufwändiger ist, liegt der Schwerpunkt von B-Tree auf der Lösung von Engpässen bei der Festplattenleistung, sodass die Kosten für die Datensuche auf einem einzelnen Knoten vernachlässigt werden können.

2. B-Baum – Mehrweg-Balance-Suchbaum

B-Baum ist ein M-Weg-Suchbaum, der hauptsächlich zur Lösung des Ungleichgewichts des M-Weg-Suchbaums verwendet wird Der Baum wird höher und führt dazu, dass der Binärbaum zu einer verknüpften Liste degeneriert. Die Leistungsprobleme sind die gleichen. B-Tree stellt das Gleichgewicht des M-Wege-Suchbaums sicher, indem es die Knoten jeder Ebene steuert und anpasst, z. B. Knotentrennung, Knotenzusammenführung, Aufteilung der übergeordneten Knoten nach oben, wenn eine Ebene voll ist, um neue Ebenen hinzuzufügen, und andere Vorgänge.

Im B-Baum ist jeder Knoten ein Plattenblock (Seite), und die Reihenfolge oder Pfadnummer M gibt die maximale Anzahl untergeordneter Knoten im Knoten an. Jeder Nicht-Blattknoten speichert Schlüsselwörter und Zeiger auf Teilbäume. Die spezifische Nummer lautet: M-Ordnung B-Baum, jeder Nicht-Blattknoten speichert M-1-Schlüsselwörter und M-Zeiger auf Teilbäume. Das Bild zeigt ein schematisches Diagramm der B-Baum-Struktur 5. Ordnung:

Lassen Sie uns gemäß der obigen Abbildung einen Blick auf den Unterschied zwischen B+-Baum und B-Baum werfen:

(2) Im B+-Baum speichern Nicht-Blattknoten nur Schlüsselwerte, während B-Baumknoten beide speichern Schlüsselwerte und Daten speichern.

Die Seitengröße ist fest und die Standardseitengröße in InnoDB beträgt 16 KB. Wenn keine Daten gespeichert werden, werden mehr Schlüsselwerte gespeichert, die Reihenfolge des entsprechenden Baums wird größer und der Baum wird kürzer und dicker. Infolgedessen ist die Anzahl der Datenträger-E/A-Suchen erforderlich Auch die Effizienz der Datenabfrage wird wieder reduziert.

Wenn außerdem ein Knoten unseres B+-Baums 1000 Schlüsselwerte speichern kann, kann der dreischichtige B+-Baum 1000 × 1000 × 1000 = 1 Milliarde Daten speichern. Im Allgemeinen befindet sich der Root-Knoten im Speicher (es ist nicht erforderlich, die Festplatte zu lesen, wenn der Root-Knoten zum ersten Mal abgerufen wird). Daher benötigen wir im Allgemeinen nur 2 Festplatten-IOs, um nach 1 Milliarde Daten zu suchen.

(2) Alle Daten im B+-Baumindex werden in Blattknoten gespeichert und die Daten sind der Reihe nach angeordnet.

B+ Die Seiten im Baum sind durch eine zweiseitig verknüpfte Liste verbunden, und die Daten in den Blattknoten sind durch eine einseitig verknüpfte Liste verbunden. Auf diese Weise können alle Daten in der Tabelle gefunden werden. B+-Bäume machen Bereichsabfragen, Sortierabfragen, Gruppenabfragen und Deduplizierungsabfragen extrem einfach. Da die Daten im B-Baum auf verschiedene Knoten verteilt sind, ist dies nicht einfach zu erreichen.

Das obige ist der detaillierte Inhalt vonWas ist der Unterschied zwischen B-Tree-Index und B+-Tree-Index in MySQL?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!