
a Es ist ein Binärbaum (jeder Knoten hat höchstens zwei untergeordnete Knoten)
b Knoten in diesem Baum# 🎜🎜#
Alle Knotenwerte im linken Teilbaum Der Fall gleicher Werte wird in binären Suchbäumen im Allgemeinen nicht berücksichtigt (Elemente sind keine Wiederholungen). Der Suchbaum im JDK hat nicht den gleichen Wert (TreeMap-Schlüssel)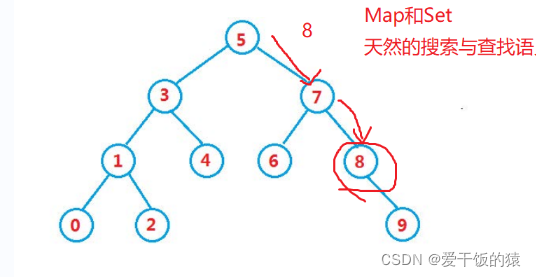 #🎜🎜 #Das größte Merkmal: Es ist auch eine Methode, um zu bestimmen, ob es sich um einen Suchbaum handelt# 🎜🎜#
#🎜🎜 #Das größte Merkmal: Es ist auch eine Methode, um zu bestimmen, ob es sich um einen Suchbaum handelt# 🎜🎜#
logN =》 Mit „Baum“ verknüpfen
2. Schlüsseloperationen
Wenn 58 gelöscht wird, werden sowohl der linke als auch der rechte Teilbaum davon gelöscht Die Knoten sind leer der aktuelle Wurzelknoten mit 58 als neuer Knoten nach dem Löschen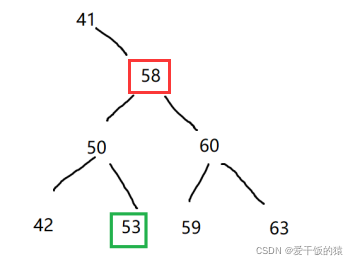 Vorgänger: mit 58 Der letzte Knoten mit weniger als 58 im BST hat seine Wurzel bei 58->53
Vorgänger: mit 58 Der letzte Knoten mit weniger als 58 im BST hat seine Wurzel bei 58->53
Nachfolger: Der erste Knoten größer als 58 im BST wurzelt bei 58->59
#🎜 🎜#Wenn wir den Nachfolgeknoten verwenden, verbinden Sie zuerst RemoveMin(root.right) und dann eine Verbindung mit root.left
TreeNode successor = findMin(root.right); successor.right = removeMin(root.right); successor.left = root.left;
import java.util.NoSuchElementException;
/**
* 基于整型的
* 普通的二分搜索树
*/
public class BST {
private class TreeNode{
private int val;
private TreeNode left;
private TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
private int size;
private TreeNode root;
/**
* 向以root为根的BST中插入一个新的结点val
* @param val
*/
public void add(int val){
root = add(root,val);
}
private TreeNode add(TreeNode root, int val) {
if(root == null){
//创建一个新节点
TreeNode newNode = new TreeNode(val);
size++;
return newNode;
}
//左子树插入
if(val < root.val){
root.left = add(root.left,val);
}
//右子树插入
if(val > root.val){
root.right = add(root.right,val);
}
return root;
}
/**
* 判断当前以root为根的BST中是否包含了val
* @param val
* @return
*/
public boolean contains(int val){
return contains(root,val);
}
private boolean contains(TreeNode root, int val) {
if(root == null){
return false;
}
if(val == root.val){
//找到了
return true;
}else if(val < root.val){
//递归左子树查找
return contains(root.left,val);
}else{
//递归右子树查找
return contains(root.right,val);
}
}
/**
* 找到最小值
* @return
*/
public int findMin(){
//判空
if(root == null){
//抛出一个空指针异常
throw new NoSuchElementException("root is empty! cannot find min");
}
TreeNode minNode = findMin(root);
return minNode.val;
}
private TreeNode findMin(TreeNode root) {
//当此节点左子树为空,说明此节点是最小值
if(root.left == null){
return root;
}
//递归访问左子树
return findMin(root.left);
}
/**
* 找到最大值
* @return
*/
public int findMax(){
//判空
if(root == null){
throw new NoSuchElementException("root is empty! cannot find max");
}
TreeNode maxNode = findMax(root);
return maxNode.val;
}
private TreeNode findMax(TreeNode root) {
//当此节点右子树为空,说明此节点是最大值
if(root.right == null){
return root;
}
//递归访问右子树
return findMax(root.right);
}
/**
* 在当前BST中删除最小值节点,返回删除的最小值
* @return
*/
public int removeMin(){
int min =findMin();
root = removeMin(root);
return min;
}
private TreeNode removeMin(TreeNode root) {
if(root.left == null){
TreeNode right = root.right;
//找到最小值,删除节点
root = root.left = null;
size--;
return right;
}
root.left = removeMin(root.left);
return root;
}
/**
* 在当前BST中删除最大值节点,返回删除的最大值
* @return
*/
public int removeMax(){
int max = findMax();
root = removeMax(root);
return max;
}
//在当前以root为根的BST中删除最小值所在的节点,返回删除后的树根
private TreeNode removeMax(TreeNode root) {
if(root.right == null){
TreeNode right = root.right;
//找到最大值,删除节点
root = root.right = null;
size--;
return right;
}
root.right = findMax(root.right);
return root;
}
/**
* 在当前以root为根节点的BST中删除值为val的节点
* 返回删除后的新的根节点
* @return
*/
public void removeValue(int value){
root = removeValue(root,value);
}
private TreeNode removeValue(TreeNode root, int value) {
if(root == null){
throw new NoSuchElementException("root is empty! cannot find remove");
}else if(value < root.val){
root.left = removeValue(root.left,value);
return root;
}else if(value > root.val){
root.right = removeValue(root.right,value);
return root;
}else {
//此时value == root.value
if(root.left == null){
//删除最小数
TreeNode right = root.right;
root = root.right = null;
size--;
return right;
}
if(root.right == null){
//删除最大数
TreeNode left = root.left;
root = root.left =null;
size--;
return left;
}
//找到当前该删除节点的前驱或者后继节点作为删除后的新节点
//当我们使用后继节点时,先连removeMin(root.right),在连root.left
TreeNode successor = findMin(root.right);
successor.right = removeMin(root.right);
successor.left = root.left;
return successor;
}
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
generateBSTString(root,0,sb);
return sb.toString();
}
//直观打印,可以看到树的深度
private void generateBSTString(TreeNode root, int height, StringBuilder sb) {
if(root == null){
sb.append(generateHeightString(height)).append("NULL\n");
return;
}
sb.append(generateHeightString(height)).append(root.val).append("\n");
generateBSTString(root.left,height+1,sb);
generateBSTString(root.right,height+1,sb);
}
private String generateHeightString(int height) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < height; i++) {
sb.append("--");
}
return sb.toString();
}
}Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen binären Suchbaum in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




