Bildkanten beziehen sich auf die Pixelmenge im Bild, bei der sich die Graustufen der umgebenden Pixel, die das Objekt ausdrücken, Schritt für Schritt ändern.
An der Kreuzung zweier benachbarter Bereiche mit unterschiedlichen Graustufen im Bild muss es einen schnellen Übergang von Graustufen oder Sprüngen geben. Sie entsprechen den Positionen der Kanten jedes Bereichs im Bild. Wie Richtung, Stufeneigenschaften, Form usw. ändern sich Pixel entlang der Kante langsam, während sich Pixel senkrecht zur Kantenrichtung drastisch ändern.
Die meisten Informationen im Bild konzentrieren sich auf die Kanten. Sobald die Kanten bestimmt sind, wird tatsächlich die Segmentierung verschiedener Bereiche erreicht.
Das Finden von Kanten erfordert häufig die Hilfe einiger Kantenerkennungsoperatoren. Einige dieser Operatoren sind Operatoren, die auf Ableitungen erster Ordnung basieren, und einige sind Differentialoperatoren zweiter Ordnung.
Roberts-Operator, Prewitt-Operator, Sobel-Operator Sie enthalten Vorlagen in x- und y-Richtung. Jede Vorlage reagiert nur auf die entsprechende Richtung, hat eine offensichtliche Ausgabe in diese Richtung und reagiert kaum auf Änderungen in andere Richtungen. Im Folgenden sind einige gängige Differentialoperatoren erster Ordnung und ihre Eigenschaften aufgeführt:
| Operatorname | Eigenschaften |
|---|---|
| Einfacher Differentialoperator | ist empfindlich gegenüber Rauschen und hat einen gewissen Verstärkungseffekt auf Rauschen |
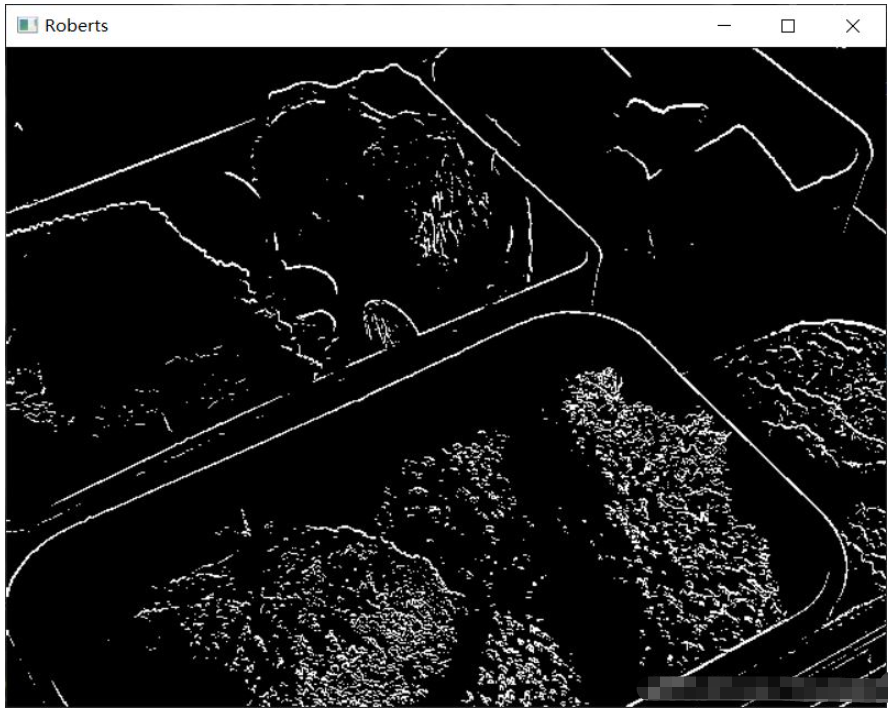
| Roberts-Operator | hat einen geringen Rauschunterdrückungseffekt und seine Kantenerkennungsfähigkeit ist besser als die eines einfachen Differentialoperators |
| Prewitt-Operator | kann den Einfluss von Rauschen wirksam unterdrücken und gleichzeitig Kantenpunkte erkennen |
| Sobel-Operator | Die erhaltene Kante ist breiter und der Rauschunterdrückungseffekt ist stärker. |
| Canny-Operator | Die erkannte Kantenposition ist genau und die Kante ist schmal . Prewitt-Operator |
4 Breite.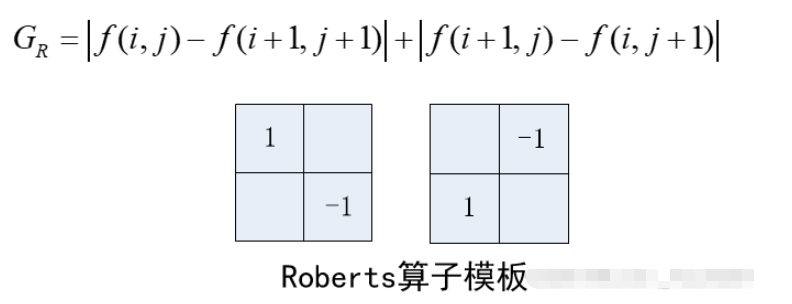 
Die Implementierung des Algorithmus ist in die folgenden 4 Schritte unterteilt:
Verwenden Sie den Gaußschen Filter, um das Bild zu glätten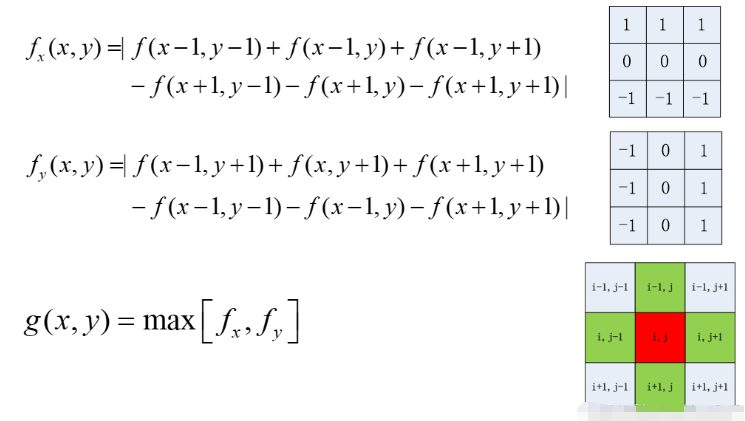 
Leitung der Nichtlinearität der Gradientenamplitude. Maximale Unterdrückung.
Verwenden Sie einen Dual-Schwellenwert-Algorithmus, um Kanten zu erkennen und zu verbinden zweidimensional Der Tutor-Operator erster Ordnung reagiert sehr empfindlich auf Bildrauschen, und die erkannten Kanten sind oft doppelte Pixel breit und haben keine Richtungsinformationen. Daher wird der Laplace-Operator selten direkt zum Erkennen von Kanten verwendet, sondern hauptsächlich Bestimmen Sie für bekannte Kanten nach einem Pixel, ob sich das Pixel in einem dunklen oder hellen Bereich des Bildes befindet. Darüber hinaus bildet der Differenzoperator erster Ordnung einen großen Gradientenwert in einem weiten Bereich, sodass er nicht genau positioniert werden kann, während der Nulldurchgangspunkt des Differenzoperators zweiter Ordnung zur genauen Lokalisierung der Kante verwendet werden kann.
Das Rauschen des Laplace-Operators ist offensichtlich größer als das des Sobel-Operators, aber seine Kanten sind viel dünner als die von Sobel, und die Laplace-Transformation ist als Differentialoperator zweiter Ordnung besonders rauschempfindlich und erzeugt Doppelkanten und kann die Kantenrichtung nicht erkennen.
Roberts_kernel_x = np.array([[-1, 0], [0, 1]], dtype=int) Roberts_kernel_y = np.array([[0, -1], [1, 0]], dtype=int)
2. Prewitt-Kantenerkennung
3 , Sobel Kantenerkennung
Sobel-Funktion:
Canny-Funktion:
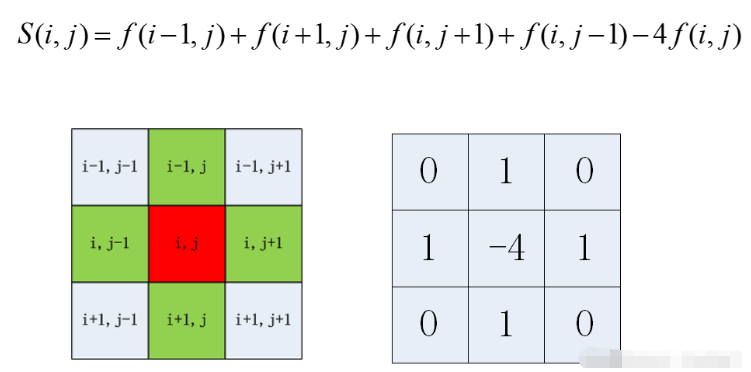
5. Laplace-Kantenerkennung
Roberts_kernel_x = np.array([[-1, 0], [0, 1]], dtype=int) Roberts_kernel_y = np.array([[0, -1], [1, 0]], dtype=int)Nach dem Login kopierenNach dem Login kopierenDas obige ist der detaillierte Inhalt vonSo verwenden Sie Python zur Bildkantenerkennung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
