Beispiel für eine Hauptkomponentenanalyse in Python
Beispiel zur Hauptkomponentenanalyse in Python
Die Hauptkomponentenanalyse (PCA) ist eine häufig verwendete Methode zur Reduzierung der Datendimensionalität. Sie kann die Dimensionalität hochdimensionaler Daten auf niedrige Dimensionen reduzieren und so viele Datenvariationsinformationen wie möglich beibehalten. Python bietet viele Bibliotheken und Tools zum Implementieren von PCA. In diesem Artikel wird anhand eines Beispiels vorgestellt, wie die sklearn-Bibliothek in Python zum Implementieren von PCA verwendet wird.
Zuerst müssen wir einen Datensatz vorbereiten. In diesem Artikel wird der Iris-Datensatz verwendet, der 150 Beispieldaten enthält. Jede Probe verfügt über 4 Merkmalswerte (die Länge und Breite des Kelchs, die Länge und Breite der Blütenblätter) und eine Beschriftung (die Art von). Irisblume). Unser Ziel ist es, die Dimensionalität dieser vier Merkmale zu reduzieren und die wichtigsten Hauptkomponenten zu finden.
Zuerst müssen wir die notwendigen Bibliotheken und Datensätze importieren.
from sklearn.datasets import load_iris from sklearn.decomposition import PCA import matplotlib.pyplot as plt iris = load_iris() X = iris.data y = iris.target
Jetzt können wir ein PCA-Objekt erstellen und es anwenden.
pca = PCA(n_components=2) X_pca = pca.fit_transform(X)
Das PCA-Objekt setzt hier n_components=2, was bedeutet, dass wir unsere verarbeiteten Daten nur auf einer zweidimensionalen Ebene anzeigen möchten. Wir wenden fit_transform auf die Originaldaten X an und erhalten den verarbeiteten Datensatz X_pca.
Jetzt können wir die Ergebnisse grafisch darstellen.
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
plt.xlabel('Component 1')
plt.ylabel('Component 2')
plt.show()In dieser Abbildung können wir die Verteilung des Iris-Datensatzes im reduzierten zweidimensionalen Raum sehen. Jeder Punkt stellt ein Muster einer Irisblume dar und die Farbe stellt die Art der Irisblume dar.
Jetzt wollen wir sehen, was die Hauptzutaten sein sollten.
print(pca.components_)
Dadurch werden zwei Vektoren namens „Komponente 1“ und „Komponente 2“ ausgegeben.
[[ 0,36158968 -0,08226889 0,85657211 0,35884393]
[-0,65653988 -0,72971237 0,1757674 0,07470647]]
Jedes Element stellt ein Merkmal dar ursprüngliches Datengewicht. Mit anderen Worten: Wir können uns Hauptkomponenten als Vektoren vorstellen, die zur linearen Kombination der ursprünglichen Merkmale verwendet werden. Jeder Vektor im Ergebnis ist ein Einheitsvektor.
Wir können auch das Ausmaß der Varianz in den Daten betrachten, die durch jede Komponente erklärt werden.
print(pca.explained_variance_ratio_)
Diese Ausgabe zeigt den Anteil der Varianz in den Daten, die durch jede Komponente erklärt wird.
[0,92461621 0,05301557]
Wir können sehen, dass diese beiden Komponenten insgesamt 94 % der Varianz in den Daten erklären. Dadurch können wir die Eigenschaften der Daten sehr genau erfassen.
Zu beachten ist, dass PCA alle Funktionen aus den Originaldaten entfernt. Wenn wir bestimmte Funktionen beibehalten müssen, müssen wir sie daher manuell entfernen, bevor wir PCA anwenden.
Dies ist ein Beispiel für die Implementierung von PCA mithilfe der sklearn-Bibliothek in Python. PCA kann auf alle Arten von Daten angewendet werden und hilft uns, die wichtigsten Komponenten aus hochdimensionalen Daten zu entdecken. Wenn Sie den Code in diesem Artikel verstehen, können Sie PCA auch auf Ihre eigenen Datensätze anwenden.
Das obige ist der detaillierte Inhalt vonBeispiel für eine Hauptkomponentenanalyse in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1391
1391
 52
52
 Lesen Sie CSV-Dateien und führen Sie eine Datenanalyse mit Pandas durch
Jan 09, 2024 am 09:26 AM
Lesen Sie CSV-Dateien und führen Sie eine Datenanalyse mit Pandas durch
Jan 09, 2024 am 09:26 AM
Pandas ist ein leistungsstarkes Datenanalysetool, das verschiedene Arten von Datendateien problemlos lesen und verarbeiten kann. Unter diesen sind CSV-Dateien eines der gebräuchlichsten und am häufigsten verwendeten Datendateiformate. In diesem Artikel wird erläutert, wie Sie mit Pandas CSV-Dateien lesen und Datenanalysen durchführen, und es werden spezifische Codebeispiele bereitgestellt. 1. Importieren Sie die erforderlichen Bibliotheken. Zuerst müssen wir die Pandas-Bibliothek und andere möglicherweise benötigte verwandte Bibliotheken importieren, wie unten gezeigt: importpandasaspd 2. Lesen Sie die CSV-Datei mit Pan
 Einführung in Datenanalysemethoden
Jan 08, 2024 am 10:22 AM
Einführung in Datenanalysemethoden
Jan 08, 2024 am 10:22 AM
Gängige Datenanalysemethoden: 1. Vergleichende Analysemethode; 3. Methode der Trendanalyse; , Hauptkomponentenanalysemethode 9. Streuanalysemethode; 10. Matrixanalysemethode; Detaillierte Einführung: 1. Vergleichende Analysemethode: Vergleichende Analyse von zwei oder mehr Daten, um die Unterschiede und Muster zu finden. 2. Strukturelle Analysemethode: Eine Methode zur vergleichenden Analyse zwischen jedem Teil des Ganzen , usw.
 Verwendung der Funktion sqrt() in Python
Feb 21, 2024 pm 03:09 PM
Verwendung der Funktion sqrt() in Python
Feb 21, 2024 pm 03:09 PM
Verwendung und Codebeispiele der Funktion sqrt() in Python 1. Funktion und Einführung der Funktion sqrt() In der Python-Programmierung ist die Funktion sqrt() eine Funktion im Mathematikmodul und ihre Funktion besteht darin, die Quadratwurzel von zu berechnen eine Zahl. Die Quadratwurzel bedeutet, dass eine mit sich selbst multiplizierte Zahl dem Quadrat der Zahl entspricht, d. h. x*x=n, dann ist x die Quadratwurzel von n. Zur Berechnung der Quadratwurzel kann im Programm die Funktion sqrt() verwendet werden. 2. So verwenden Sie die Funktion sqrt() in Python, sq
 11 Grundverteilungen, die Datenwissenschaftler in 95 % der Fälle verwenden
Dec 15, 2023 am 08:21 AM
11 Grundverteilungen, die Datenwissenschaftler in 95 % der Fälle verwenden
Dec 15, 2023 am 08:21 AM
Im Anschluss an die letzte Bestandsaufnahme von „11 Basisdiagramme, die Datenwissenschaftler in 95 % der Zeit verwenden“ stellen wir Ihnen heute 11 Basisverteilungen vor, die Datenwissenschaftler in 95 % der Zeit verwenden. Die Beherrschung dieser Verteilungen hilft uns, die Natur der Daten besser zu verstehen und bei der Datenanalyse und Entscheidungsfindung genauere Schlussfolgerungen und Vorhersagen zu treffen. 1. Normalverteilung Die Normalverteilung, auch Gaußsche Verteilung genannt, ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Es hat eine symmetrische glockenförmige Kurve mit dem Mittelwert (μ) als Mittelpunkt und der Standardabweichung (σ) als Breite. Die Normalverteilung hat in vielen Bereichen wie Statistik, Wahrscheinlichkeitstheorie und Ingenieurwesen einen wichtigen Anwendungswert.
 So führen Sie Bildverarbeitung und -erkennung in Python durch
Oct 20, 2023 pm 12:10 PM
So führen Sie Bildverarbeitung und -erkennung in Python durch
Oct 20, 2023 pm 12:10 PM
So führen Sie Bildverarbeitung und -erkennung in Python durch Zusammenfassung: Moderne Technologie hat Bildverarbeitung und -erkennung in vielen Bereichen zu einem wichtigen Werkzeug gemacht. Python ist eine einfach zu erlernende und zu verwendende Programmiersprache mit umfangreichen Bildverarbeitungs- und Erkennungsbibliotheken. In diesem Artikel wird die Verwendung von Python für die Bildverarbeitung und -erkennung vorgestellt und spezifische Codebeispiele bereitgestellt. Bildverarbeitung: Bei der Bildverarbeitung werden verschiedene Vorgänge und Transformationen an Bildern durchgeführt, um die Bildqualität zu verbessern, Informationen aus Bildern zu extrahieren usw. PIL-Bibliothek in Python (Pi
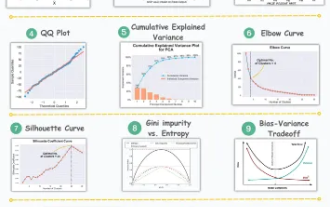 11 erweiterte Visualisierungen für Datenanalyse und maschinelles Lernen
Oct 25, 2023 am 08:13 AM
11 erweiterte Visualisierungen für Datenanalyse und maschinelles Lernen
Oct 25, 2023 am 08:13 AM
Visualisierung ist ein leistungsstarkes Werkzeug, um komplexe Datenmuster und Beziehungen auf intuitive und verständliche Weise zu kommunizieren. Sie spielen eine wichtige Rolle bei der Datenanalyse und liefern Erkenntnisse, die aus Rohdaten oder herkömmlichen numerischen Darstellungen oft nur schwer zu erkennen sind. Visualisierung ist für das Verständnis komplexer Datenmuster und -beziehungen von entscheidender Bedeutung. Wir stellen die 11 wichtigsten und unverzichtbarsten Diagramme vor, die dabei helfen, die Informationen in den Daten offenzulegen und komplexe Daten verständlicher und aussagekräftiger zu machen. 1. KSPlotKSPlot wird zur Bewertung von Verteilungsunterschieden verwendet. Die Kernidee besteht darin, den maximalen Abstand zwischen den kumulativen Verteilungsfunktionen (CDF) zweier Verteilungen zu messen. Je kleiner der maximale Abstand, desto wahrscheinlicher ist es, dass sie zur gleichen Verteilung gehören. Daher wird es hauptsächlich als „System“ zur Bestimmung von Verteilungsunterschieden interpretiert.
 Maschinelles Lernen und Datenanalyse mit der Go-Sprache
Nov 30, 2023 am 08:44 AM
Maschinelles Lernen und Datenanalyse mit der Go-Sprache
Nov 30, 2023 am 08:44 AM
In der heutigen intelligenten Gesellschaft sind maschinelles Lernen und Datenanalyse unverzichtbare Werkzeuge, die den Menschen helfen können, große Datenmengen besser zu verstehen und zu nutzen. Auch in diesen Bereichen hat sich die Go-Sprache zu einer Programmiersprache entwickelt, die aufgrund ihrer Geschwindigkeit und Effizienz die erste Wahl vieler Programmierer ist. In diesem Artikel wird die Verwendung der Go-Sprache für maschinelles Lernen und Datenanalyse vorgestellt. 1. Das Ökosystem der Go-Sprache für maschinelles Lernen ist nicht so reichhaltig wie Python und R. Da jedoch immer mehr Menschen beginnen, es zu verwenden, gibt es einige Bibliotheken und Frameworks für maschinelles Lernen
 Verwendung von ECharts und PHP-Schnittstellen zur Implementierung der Datenanalyse und Vorhersage statistischer Diagramme
Dec 17, 2023 am 10:26 AM
Verwendung von ECharts und PHP-Schnittstellen zur Implementierung der Datenanalyse und Vorhersage statistischer Diagramme
Dec 17, 2023 am 10:26 AM
Verwendung von ECharts und PHP-Schnittstellen zur Implementierung der Datenanalyse und Vorhersage statistischer Diagramme. Datenanalyse und -vorhersage spielen in verschiedenen Bereichen eine wichtige Rolle. Sie können uns helfen, die Trends und Muster von Daten zu verstehen und Referenzen für zukünftige Entscheidungen bereitzustellen. ECharts ist eine Open-Source-Datenvisualisierungsbibliothek, die umfangreiche und flexible Diagrammkomponenten bereitstellt, die mithilfe der PHP-Schnittstelle Daten dynamisch laden und verarbeiten können. In diesem Artikel wird die Implementierungsmethode der statistischen Diagrammdatenanalyse und -vorhersage basierend auf ECharts und der PHP-Schnittstelle vorgestellt und bereitgestellt




