Eine einfache Möglichkeit, Kurven mithilfe der Canvas_html5-Tutorial-Tipps von HTML5 zu zeichnen

Die Kurvenmethode, die mit Canvas2D geliefert wird
Kürzlich habe ich mich mit der Berechnung von 3D-Weichkörpern beschäftigt und versuche daher, etwas Wissen nachzuholen. Dabei handelt es sich häufig um numerische Analysen, hauptsächlich um verschiedene Interpolationsalgorithmen für Kurven. Plötzlich fiel mir ein, dass Canvas2D selbst auch Kurven zeichnen kann, und zwar unter Verwendung quadratischer und kubischer Bezier-Kurven. Tatsächlich habe ich diese Methode noch nie verwendet, also versuchen wir es jetzt ~
In diesem Artikel geht es nur um das einfache Zeichnen von Kurven, und ich werde nicht auf viele komplizierte Prinzipien eingehen. Darüber hinaus ist das Prinzip der Bezier-Kurve sehr einfach. Sie können es verstehen, indem Sie einen Blick auf Wikipedia werfen. Tatsächlich verwenden viele einfache Kurvenzeichnungen in Zeichenwerkzeugen Bezier-Kurven. Wenn Sie die Kurven in den Zeichenwerkzeugen von Windows verwendet haben, müssen Sie mit ihnen vertraut sein. Sie können zunächst eine gerade Linie ziehen und dann auf eine bestimmte Position klicken, um die gerade Linie zu verzerren. Die anfängliche Ziehaktion besteht darin, die beiden Scheitelpunkte der Kurve zu bestimmen, und die Klickaktion besteht darin, einen Zwischenpunkt hinzuzufügen. Das mit Windows gelieferte Zeichenwerkzeug verwendet eine kubische Bezier-Kurve, und Sie können zwei Zwischenpunkte hinzufügen. Die Bezier-Kurve unterscheidet sich von der allgemeinen Polynominterpolation. Ihr Mittelpunkt wird nur als Kontrollpunkt verwendet, nicht als Scheitelpunkt, durch den die Kurve verlaufen muss. Und es können auch geschlossene Kurven erstellt werden. Canvas2D bietet zwei Methoden zum Zeichnen von Kurven
　quadraticCurveTo: Quadratische Bezier-Kurve
　bezierCurveTo: Kubische Bezier-Kurve
Linien werden ausgehend von der aktuellen Position gezeichnet. Nachdem Sie die Startposition der Kurve festgelegt haben, benötigen Sie auch den Mittelpunkt und die Endposition. Übergeben Sie diese Positionskoordinaten einfach an die Zeichenfunktion. Beispielsweise erfordert eine quadratische Bezier-Kurve einen Zwischenpunkt und eine Endposition, sodass zwei Koordinaten an die Funktion quadraticCurveTo übergeben werden müssen. Die Koordinaten bestehen aus x und y, was bedeutet, dass diese Funktion 4 Parameter hat. bezierCurveTo ist dasselbe, außer dass es zwei Zwischenpunkte hat. Lassen Sie es uns unten verwenden

CSS-CodeInhalt in die Zwischenablage kopieren

1. "canvas" width=" 200" Höhe="200">
2. <script> </span></li>var g=canvas.getContext(<li class="alt"> <span>"2d"</span><span class="string">); </span><span>//Gewöhnliche gerade Linie </span> </li> <li><span>g.beginPath(); </span></li> <li class="alt"><span>g.strokeStyle=</span></li>"#CCC"<li> <span> </span><span class="string"> </span><span>g.moveTo(0,0); </span> </li> <li class="alt"><span>g.lineTo(200,0); </span></li> <li><span>g.lineTo(0,200); </span></li> <li class="alt"><span>g.lineTo(200,200); </span></li> <li><span>g.streich(); </span></li> <li class="alt"><span>//Bez-Kurve </span></li> <li><span>g.beginPath(); </span></li> <li class="alt"><span>g.strokeStyle=</span></li>"#F00"<li> <span>; </span><span class="string">g.moveTo(0,0); </span><span> </span> </li>g.bezierCurveTo(200,0, 0,200, 200,200); <li class="alt"><span>g.streich(); </span></li> <li><span></script>
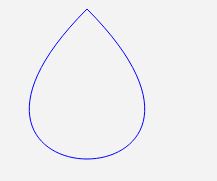
4. Dies ergibt vier Punkte gemäß der Z-förmigen Flugbahn und zeichnet gewöhnliche gerade Linien und Bezier-Kurven. Dies ist nur eine gewöhnliche Kurve. Das Tolle an der Bezier-Kurve ist, dass sie geschlossene Kurven wie diesen Code zeichnen kann

CSS-Code

Inhalt in die Zwischenablage kopieren

g.beginPath();

g.strokeStyle=
1. "#00F";
g.moveTo(100,0);
2. g.bezierCurveTo(-100,200, 300,200, 100,0);
g.streich();

4. 

   Setzen Sie die Start- und Endposition der kubischen Bezier-Kurve auf denselben Punkt, um eine geschlossene Kurve zu zeichnen. Da die Interpolationsrichtung der Bezier-Kurve nicht der Koordinatenachse folgt, kann eine geschlossene Kurve gezeichnet werden. Wenn wir möchten, dass die Polynominterpolation eine geschlossene Kurve zeichnet, müssen wir die Parameter konvertieren und zum Abschluss das Polarkoordinatensystem verwenden.
   Die Beispiele, die ich verwende, sind alle kubische Bezier-Kurven. Tatsächlich ist der zweite Schritt derselbe, aber ohne den Mittelpunkt kann ich nicht zeichnen, was ich möchte. Ich werde nicht zu viel darauf eingehen, das war's für diesen Artikel = =. .