 Backend-Entwicklung
Backend-Entwicklung
 PHP-Tutorial
PHP-Tutorial
 Detaillierte Erklärung des längsten gemeinsamen Teilsequenzalgorithmus in PHP
Detaillierte Erklärung des längsten gemeinsamen Teilsequenzalgorithmus in PHP
Detaillierte Erklärung des längsten gemeinsamen Teilsequenzalgorithmus in PHP
Detaillierte Erklärung des Algorithmus für die längste gemeinsame Teilsequenz in PHP
Die längste gemeinsame Teilsequenz (LCS) ist ein allgemeiner String-Matching-Algorithmus, der hauptsächlich zum Vergleichen der Ähnlichkeit zweier Strings verwendet wird. In PHP kann der LCS-Algorithmus durch die Idee der dynamischen Programmierung implementiert werden. Das Prinzip und die Code-Implementierung des Algorithmus werden im Folgenden ausführlich vorgestellt.
- Algorithmusprinzip
Die Kernidee des Algorithmus für die längste gemeinsame Teilfolge besteht darin, für zwei beliebige Zeichenfolgen X und Y die längste gemeinsame Teilfolge L zu finden, sodass L eine Teilfolge von X und Y ist und keine gemeinsame Teilfolge existiert länger als L. Unter der Idee der dynamischen Programmierung können wir ein zweidimensionales Array dpi verwenden, um die Länge der längsten gemeinsamen Teilsequenz der ersten i Zeichen der Zeichenfolge X und der ersten j Zeichen der Zeichenfolge Y darzustellen.
Konkret können wir die folgenden Schritte ausführen, um die längste gemeinsame Teilfolge zu lösen:
1) Initialisieren Sie ein dp-Array, wobei dpi das Maximum der ersten i Zeichen der Zeichenfolge X und der ersten j Zeichen der Zeichenfolge Y darstellt. Die Länge von die lange gemeinsame Teilfolge.
2) Durchlaufen Sie jedes Zeichen der Zeichenfolgen X und Y. Wenn X[i] gleich Y[j] ist, kann der dpi-Wert durch dpi-1+1 ermittelt werden und dpi Der größere Wert in .
3) Schließlich ist dpm die Länge der längsten gemeinsamen Teilfolge der Zeichenfolgen X und Y, wobei m und n die Längen der Zeichenfolgen X und Y sind.
- Code-Implementierung
Das Folgende ist ein Codebeispiel zur Implementierung des längsten gemeinsamen Teilsequenzalgorithmus mithilfe der PHP-Sprache:
function LCS($str1, $str2)
{
$m = strlen($str1);
$n = strlen($str2);
$dp = array();
for ($i = 0; $i <= $m; $i++) {
$dp[$i][0] = 0;
}
for ($j = 0; $j <= $n; $j++) {
$dp[0][$j] = 0;
}
for ($i = 1; $i <= $m; $i++) {
for ($j = 1; $j <= $n; $j++) {
if ($str1[$i - 1] == $str2[$j - 1]) {
$dp[$i][$j] = $dp[$i - 1][$j - 1] + 1;
} else {
$dp[$i][$j] = max($dp[$i - 1][$j], $dp[$i][$j - 1]);
}
}
}
$lcs = '';
$i = $m;
$j = $n;
while ($i > 0 && $j > 0) {
if ($str1[$i - 1] == $str2[$j - 1]) {
$lcs = $str1[$i - 1] . $lcs;
$i--;
$j--;
} elseif ($dp[$i - 1][$j] > $dp[$i][$j - 1]) {
$i--;
} else {
$j--;
}
}
return $lcs;
}
$str1 = "abcdefg";
$str2 = "bcedgh";
$lcs = LCS($str1, $str2);
echo "最长公共子序列: " . $lcs;Im obigen Code initialisieren wir zunächst ein zweidimensionales Array dp und fügen seine ersten Zeilen- und ersten Spaltenelemente hinzu sind alle auf 0 gesetzt. Anschließend verwenden wir zwei verschachtelte for-Schleifen, um jedes Element im dp-Array zu berechnen. Schließlich finden wir durch Backtracking die längste gemeinsame Teilsequenz und geben sie zurück.
- Fazit
Der längste gemeinsame Teilsequenzalgorithmus ist ein effizienter String-Matching-Algorithmus, der sich zur Lösung von String-Ähnlichkeitsproblemen eignet. Durch die Idee der dynamischen Programmierung können wir die längste gemeinsame Teilfolge mit einer Zeitkomplexität von O(m*n) lösen. In PHP können wir das obige Codebeispiel verwenden, um diesen Algorithmus zu implementieren und die längste gemeinsame Teilsequenz zweier Zeichenfolgen zu erhalten.
Das obige ist der detaillierte Inhalt vonDetaillierte Erklärung des längsten gemeinsamen Teilsequenzalgorithmus in PHP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1371
1371
 52
52
 PHP 8.4 Installations- und Upgrade-Anleitung für Ubuntu und Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 Installations- und Upgrade-Anleitung für Ubuntu und Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 bringt mehrere neue Funktionen, Sicherheitsverbesserungen und Leistungsverbesserungen mit einer beträchtlichen Menge an veralteten und entfernten Funktionen. In dieser Anleitung wird erklärt, wie Sie PHP 8.4 installieren oder auf PHP 8.4 auf Ubuntu, Debian oder deren Derivaten aktualisieren. Obwohl es möglich ist, PHP aus dem Quellcode zu kompilieren, ist die Installation aus einem APT-Repository wie unten erläutert oft schneller und sicherer, da diese Repositorys in Zukunft die neuesten Fehlerbehebungen und Sicherheitsupdates bereitstellen.
 CakePHP Datum und Uhrzeit
Sep 10, 2024 pm 05:27 PM
CakePHP Datum und Uhrzeit
Sep 10, 2024 pm 05:27 PM
Um in cakephp4 mit Datum und Uhrzeit zu arbeiten, verwenden wir die verfügbare FrozenTime-Klasse.
 CakePHP arbeitet mit Datenbank
Sep 10, 2024 pm 05:25 PM
CakePHP arbeitet mit Datenbank
Sep 10, 2024 pm 05:25 PM
Das Arbeiten mit der Datenbank in CakePHP ist sehr einfach. In diesem Kapitel werden wir die CRUD-Operationen (Erstellen, Lesen, Aktualisieren, Löschen) verstehen.
 CakePHP-Datei hochladen
Sep 10, 2024 pm 05:27 PM
CakePHP-Datei hochladen
Sep 10, 2024 pm 05:27 PM
Um am Datei-Upload zu arbeiten, verwenden wir den Formular-Helfer. Hier ist ein Beispiel für den Datei-Upload.
 Besprechen Sie CakePHP
Sep 10, 2024 pm 05:28 PM
Besprechen Sie CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP ist ein Open-Source-Framework für PHP. Es soll die Entwicklung, Bereitstellung und Wartung von Anwendungen erheblich vereinfachen. CakePHP basiert auf einer MVC-ähnlichen Architektur, die sowohl leistungsstark als auch leicht zu verstehen ist. Modelle, Ansichten und Controller gu
 CakePHP erstellt Validatoren
Sep 10, 2024 pm 05:26 PM
CakePHP erstellt Validatoren
Sep 10, 2024 pm 05:26 PM
Der Validator kann durch Hinzufügen der folgenden zwei Zeilen im Controller erstellt werden.
 So richten Sie Visual Studio-Code (VS-Code) für die PHP-Entwicklung ein
Dec 20, 2024 am 11:31 AM
So richten Sie Visual Studio-Code (VS-Code) für die PHP-Entwicklung ein
Dec 20, 2024 am 11:31 AM
Visual Studio Code, auch bekannt als VS Code, ist ein kostenloser Quellcode-Editor – oder eine integrierte Entwicklungsumgebung (IDE) –, die für alle gängigen Betriebssysteme verfügbar ist. Mit einer großen Sammlung von Erweiterungen für viele Programmiersprachen kann VS Code c
 CakePHP-Protokollierung
Sep 10, 2024 pm 05:26 PM
CakePHP-Protokollierung
Sep 10, 2024 pm 05:26 PM
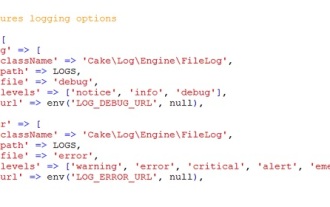
Die Anmeldung bei CakePHP ist eine sehr einfache Aufgabe. Sie müssen nur eine Funktion verwenden. Sie können Fehler, Ausnahmen, Benutzeraktivitäten und von Benutzern durchgeführte Aktionen für jeden Hintergrundprozess wie Cronjob protokollieren. Das Protokollieren von Daten in CakePHP ist einfach. Die Funktion log() wird bereitgestellt



