Auf Wiedersehen, Go-Interviewer: GMP-Modell, warum gibt es P?

Der heutige Protagonist ist eine Erweiterungsfrage (Frage) der Allzweck-GMP-Modellfrage im Go-Interview, nämlich „GMP-Modell, warum braucht es P?“

Weitere Einblicke in den Hintergrund Der Kern der Frage besteht in diesem Interview darin, zu fragen: „Warum können G und M im GMP-Modell nicht direkt gebunden werden? Das ist so problematisch. Warum ist es so problematisch? Welches Problem ist das?“ Versuchen Sie es zu lösen?

GM-Modell

Vor Go1.1 war das Planungsmodell von Go eigentlich das GM-Modell, das heißt, es gab kein P.

Heute nehme ich Sie mit, um frühere Designs zu begutachten.

Den Go1.0-Quellcode entschlüsseln

Eine Möglichkeit für uns, etwas zu verstehen, besteht darin, einen Blick auf die wichtigsten Schlüsselschritte des Go1.0.1-Scheduler-Quellcodes zu werfen Jianyu:

static void
schedule(G *gp)
{
 ...
 schedlock();
 if(gp != nil) {
  ...
  switch(gp->status){
  case Grunnable:
  case Gdead:
   // Shouldn't have been running!
   runtime·throw("bad gp->status in sched");
  case Grunning:
   gp->status = Grunnable;
   gput(gp);
   break;
  }

 gp = nextgandunlock();
 gp->readyonstop = 0;
 gp->status = Grunning;
 m->curg = gp;
 gp->m = m;
 ...
 runtime·gogo(&gp->sched, 0);
}

• Callschedlock 方法来获取全局锁。
• 获取全局锁成功后，将当前 Goroutine 状态从 Running（正在被调度） 状态修改为 Runnable（可以被调度）状态。
• 调用 gput 方法来保存当前 Goroutine 的运行状态等信息，以便于后续的使用。
• 调用 nextgandunlock 方法来寻找下一个可运行 Goroutine，并且释放全局锁给其他调度使用。
• 获取到下一个待运行的 Goroutine 后，将其运行状态修改为 Running。
• 调用 runtime·gogo

Nachdem Sie die globale Sperre erfolgreich erworben haben, ändern Sie den aktuellen Goroutine-Status von „Läuft“ (wird geplant) in den Status „Ausführbar“ (kann geplant werden).

Call Call

Nachdem Sie die nächste auszuführende Goroutine erhalten haben, ändern Sie ihren Ausführungsstatus in „Läuft“.

CallWenn wir über das GM-Modell nachdenken

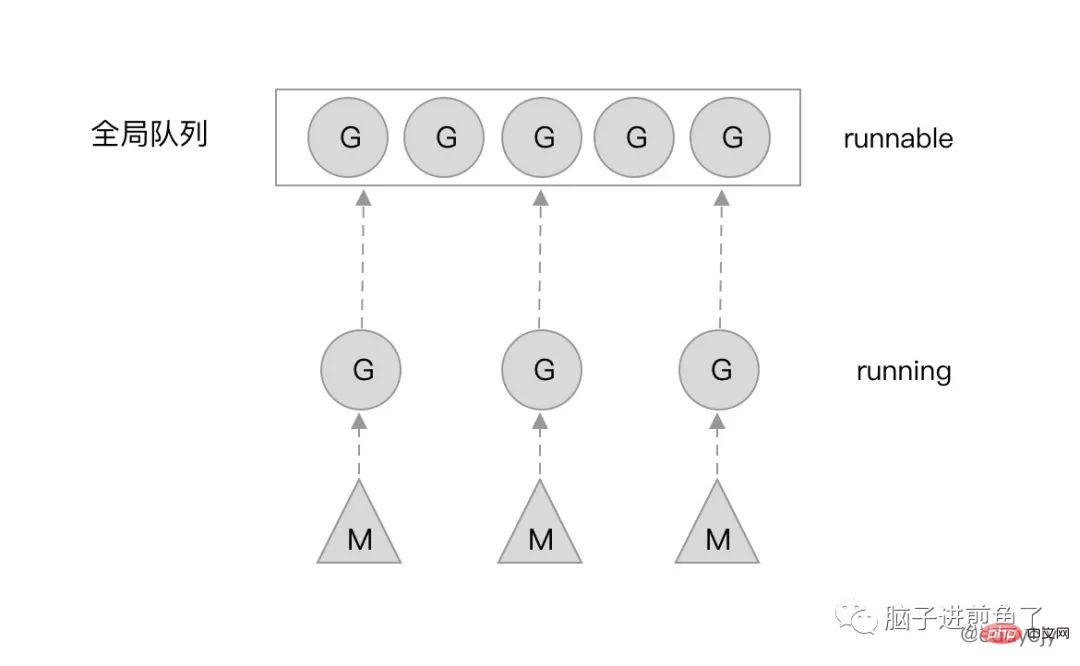
Durch die Analyse des Scheduler-Quellcodes von Go1.0.1 können wir einen interessanten Punkt finden. Das ist der Scheduler selbst (Schedule-Methode), der bei normalen Prozessen nicht zurückkehrt, das heißt, er beendet den Hauptprozess nicht.

🎜🎜🎜G-M-Modelldiagramm🎜🎜🎜 Nachdem GoroutineA abgeschlossen ist, beginnt es mit der Suche nach GoroutineB. Wenn B gefunden wird, wird das abgeschlossene Planungsrecht von A an B übergeben beginnt mit dem Scheduling, also dem Laufen. 🎜🎜Natürlich gibt es auch Gs, die blockiert (Blocked) sind. Angenommen, G führt einige System- oder Netzwerkaufrufe durch, die dazu führen, dass G ins Stocken gerät. Zu diesem Zeitpunkt wird M (System-Thread) wieder in die Kernel-Warteschlange gestellt und wartet auf eine neue Aktivierungsrunde. 🎜🎜🎜🎜Nachteile des GM-Modells🎜🎜🎜🎜Oberflächlich betrachtet scheint das GM-Modell unzerstörbar und makellos zu sein. Aber warum sollte man es ändern? 🎜🎜Im Jahr 2012 veröffentlichte Dmitry Vyukov den Artikel „Scalable Go Scheduler Design Doc“, der immer noch das Hauptziel wichtiger Forschungsartikel zum Go Scheduler ist. Er beschrieb die allgemeinen Gründe und Überlegungen im Artikel . 🎜

Der aktuelle Goroutine-Scheduler (bezogen auf das GM-Modell von Go 1.0) schränkt die Skalierbarkeit gleichzeitiger, in Go geschriebener Programme ein, insbesondere Server mit hohem Durchsatz und parallele Rechenprogramme.

Die Implementierung weist die folgenden Probleme auf:

• Es gibt einen einzigen globalen Mutex (Sched.Lock) und eine zentralisierte Zustandsverwaltung:
• Mutex muss alle Goroutine-bezogenen Vorgänge (Erstellung, Vervollständigung, Neuordnung, usw.), was zu einem ernsthaften Wettbewerb um Schlösser führt.
• Probleme bei der Bereitstellung von Goroutinen:
• Übergabe von Goroutinen (G) (G.nextg): Ausführbare Goroutinen werden häufig zwischen Arbeitsthreads (Ms) übergeben.
• Das oben Genannte kann zu erhöhter Latenz und zusätzlichem Overhead führen. Jedes M muss in der Lage sein, jedes ausführbare G auszuführen, insbesondere das M, das gerade G erstellt hat.
• Jedes M muss im Speicher (M.mcache) zwischengespeichert werden:
• führt zu einem übermäßigen Ressourcenverbrauch (jeder Mcache kann 2 MB Speichercache und andere Caches aufnehmen) und einer schlechten Datenlokalität.
• Häufiges Blockieren/Entsperren von Threads:
• Threads werden häufig blockiert und entsperrt, wenn Systemaufrufe vorhanden sind. Dies führt zu einem erheblichen zusätzlichen Leistungsaufwand.

GMP-Modell

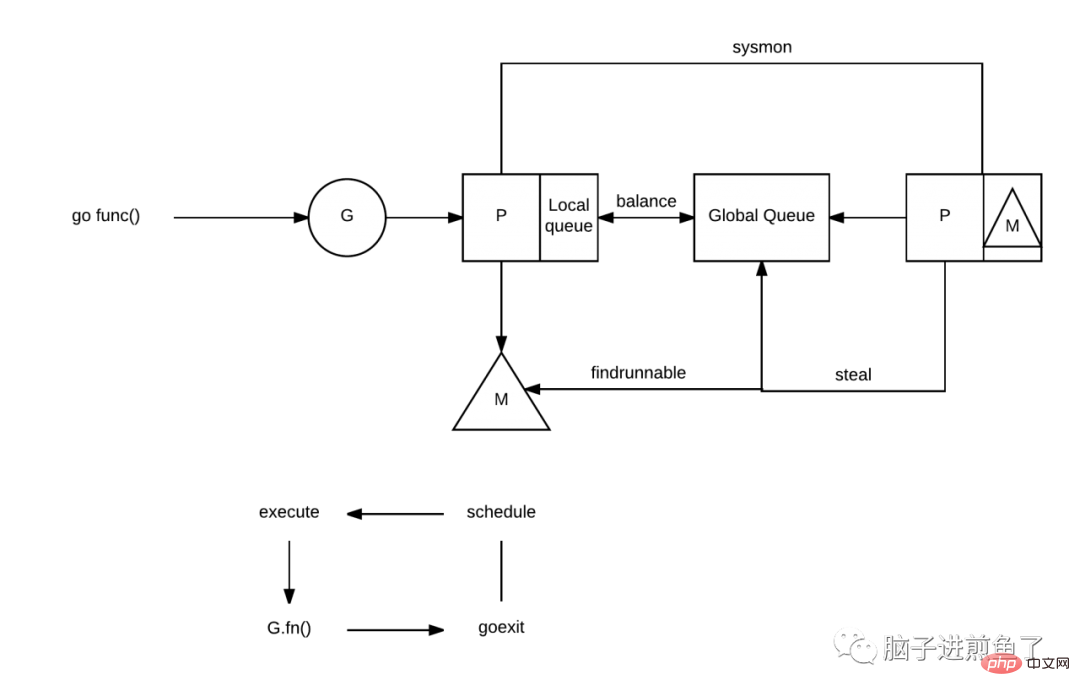
Um viele der oben genannten Probleme des GM-Modells zu lösen, fügte Dmitry Vyukov in Go1.1 eine neue P-Komponente (Prozessor) basierend auf dem GM-Modell hinzu. Und den Work Stealing-Algorithmus implementiert, um einige neu entstandene Probleme zu lösen.

GMP-Modell, im vorherigen Artikel „Go-Gruppe“ fragten Freunde: Wie viele Goroutinen sollten angemessen gesteuert werden? Wird sich dies auf GC und Planung auswirken? wurde in „“ erklärt.

Freunde, die es gut finden, können darauf achten, ich werde es hier nicht wiederholen.

Welche Änderungen wird es mit sich bringen

Welche Veränderungen wird es mit sich bringen, nachdem P hinzugefügt wurde? Lassen Sie uns ausführlicher darüber sprechen.

• Jedes P verfügt über eine eigene lokale Warteschlange, wodurch die direkte Abhängigkeit von der globalen Warteschlange erheblich verringert wird. Das Ergebnis ist eine Verringerung des Sperrwettbewerbs. Der Großteil des Leistungsaufwands des GM-Modells ist auf die Sperrkonkurrenz zurückzuführen.

• Auf der relativen Bilanz jedes P wird der Work Stealing-Algorithmus auch im GMP-Modell implementiert. Wenn die lokale Warteschlange von P leer ist, wird das ausführbare G aus der globalen Warteschlange oder der lokalen Warteschlange von gestohlen andere P zu betreiben, was den Leerlauf reduziert und die Ressourcennutzung verbessert.

Warum gibt es P?? Für M können ähnliche Funktionen erreicht werden .

Warum eine weitere P-Komponente hinzufügen?

In Kombination mit der Positionierung von M (Systemgewinde) treten in diesem Fall die folgenden Probleme auf.

Im Allgemeinen ist die Anzahl von M größer als die von P. Wie in Go beträgt die maximale Anzahl von M 10.000, und die Standardanzahl von P ist die Anzahl der CPU-Kerne. Darüber hinaus steigt M aufgrund der Eigenschaften von M weiter an, wenn es einen Systemblockierungsaufruf gibt, der M blockiert und nicht ausreicht.

• Wenn M weiter zunimmt und die lokale Warteschlange auf M gemountet ist, bedeutet dies, dass auch die lokale Warteschlange entsprechend zunimmt. Dies ist offensichtlich unvernünftig, da die Verwaltung lokaler Warteschlangen kompliziert wird und die Leistung von Work Stealing erheblich verringert wird.

• M Nach der Blockierung durch einen Systemaufruf hoffen wir, die nicht ausgeführten Aufgaben anderen zuweisen zu können, damit sie weiter ausgeführt werden können, anstatt alles zum Stoppen zu bringen, sobald es blockiert wird.

• Daher ist die Verwendung von M unvernünftig. Dann kann die Einführung einer neuen Komponente P und die Zuordnung der lokalen Warteschlange zu P dieses Problem sehr gut lösen.

Zusammenfassung

Der heutige Artikel kombiniert einige historische Situationen, Ursachenanalysen und Lösungsbeschreibungen des gesamten Go-Sprachplaners.

„GMP-Modell, warum gibt es P?“ Diese Frage ist wie ein Systemdesign-Verständnis, denn jetzt werden sich viele Leute das GMP-Modell merken oder es sofort durchgehen, um das Interview zu bewältigen. Und wir müssen lernen und verstehen, die wahren Gründe dafür zu verstehen.

Nur wenn Sie wissen, was passiert und warum es passiert, können Sie die Situation durchbrechen.

Das obige ist der detaillierte Inhalt vonAuf Wiedersehen, Go-Interviewer: GMP-Modell, warum gibt es P?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!