Tipps |. Dies ist wahrscheinlich das beste grafische NumPy-Tutorial, das ich je gesehen habe!

NumPy ist ein wichtiges Softwarepaket in Python für Datenanalyse, maschinelles Lernen und wissenschaftliches Rechnen. Es vereinfacht die Bedienung und Verarbeitung von Vektoren und Matrizen erheblich. Viele Datenverarbeitungssoftwarepakete für Python basieren auf NumPy als Kern Teil ihrer Infrastruktur (z. B. Scikit-Learn, SciPy, Pandas und Tensorflow). Zusätzlich zu den Funktionen des Data Slicing und Data Dicing bietet die Beherrschung von Numpy Entwicklern auch einen Vorteil bei der Verwendung verschiedener Datenverarbeitungsbibliotheken zum Debuggen und Behandeln komplexer Anwendungsfälle.

In diesem Artikel stellen wir die Hauptverwendungen von NumPy vor und wie es verschiedene Arten von Daten (Tabellen, Bilder, Text usw.) darstellt werden zur Eingabe für das maschinelle Lernmodell.

Array-Operationen in NumPy

Array erstellen

Wir können Erstellen Sie ein NumPy-Array (auch bekannt als das leistungsstarke Ndarray), indem Sie eine Python-Liste übergeben in np.array(). Im folgenden Beispiel wird das erstellte Array rechts angezeigt. Normalerweise möchten wir, dass NumPy den Wert des Arrays für uns initialisiert. Zu diesem Zweck stellt NumPy Funktionen wie ones(), zeros() und random.random( zur Verfügung. ). Methode. Wir müssen nur die Anzahl der Elemente übergeben:

Sobald wir das Array erstellt haben, können wir einige interessante Anwendungen damit machen, die weiter unten erklärt werden.

Arithmetische Operationen auf Arrays

Erstellen wir zwei NumPy-Arrays, genannt Daten und Einsen:

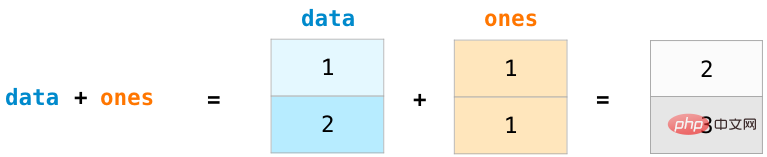
Um zwei Arrays zur Addition zu berechnen, geben Sie einfach Daten ein + Einsen, um die Daten an der entsprechenden Position hinzuzufügen (d. h. jede Datenzeile hinzuzufügen). Diese Operation ist prägnanter als der Methodencode zum Schleifenlesen des Arrays.

Natürlich können wir darauf aufbauend auch Operationen wie Subtraktion, Multiplikation und Division umsetzen:

In vielen Fällen möchten wir Operationen an Arrays und Einzelwerten durchführen (auch Operationen zwischen Vektoren und Skalaren genannt). Beispiel: Wenn das Array die Entfernung in Meilen darstellt, besteht unser Ziel darin, sie in Kilometer umzurechnen. Es kann einfach als Daten * 1.6 geschrieben werden:

NumPy weiß durch Array-Broadcasting, dass dieser Vorgang die Multiplikation jedes Elements des Arrays erfordert.

Array-Slicing-Vorgang

Wir können NumPy-Arrays wie Python-Listenoperationen indizieren und segmentieren, wie unten gezeigt:

Aggregationsfunktionen

bereitgestellt von NumP y Praktischerweise gibt es sie auch Aggregationsfunktionen, die Daten komprimieren und einige Merkmalswerte im Array zählen können:

Zusätzlich zu Funktionen wie Min, Max und Summe gibt es auch Mittelwert ( Mittelwert), prod (Datenmultiplikation) berechnet das Produkt aller Elemente, std (Standardabweichung) usw. Alle obigen Beispiele befassen sich mit Vektoren in einer Dimension. Darüber hinaus ist ein wesentlicher Teil der Schönheit von NumPy seine Fähigkeit, alle Funktionen, die wir bisher gesehen haben, auf jede Dimension anzuwenden.

Matrixoperationen in NumPy

Wir können eine Matrix erstellen, indem wir eine zwei- Dimensionsliste zu Numpy.

np.array([[1,2],[3,4]])

Darüber hinaus können Sie auch die oben erwähnten ones(), zeros() und random.random() verwenden, um Matrizen zu erstellen. Übergeben Sie einfach ein Tupel, um die Dimensionen der Matrix zu beschreiben:

Arithmetische Operationen auf Matrizen

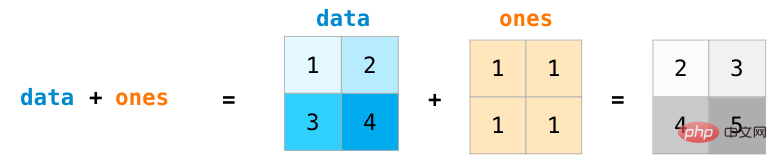
Für zwei Matrizen gleicher Größe können wir arithmetische Operatoren (+-*/) verwenden, um sie zu addieren oder zu multiplizieren. NumPy verwendet für solche Operationen positionsbezogene Operationen:

Für Matrizen unterschiedlicher Größe können wir diese arithmetischen Operationen nur ausführen, wenn die Abmessungen der beiden Matrizen gleich 1 sind (in diesem Fall verwendet NumPy Broadcast-Regeln). (Broadcast) für die Operationsverarbeitung:

Ein großer Unterschied zu arithmetischen Operationen ist die Matrixmultiplikation mit Skalarprodukt. NumPy bietet die dot()-Methode, mit der Skalarproduktoperationen zwischen Matrizen durchgeführt werden können: Die Matrizen der Operation befinden sich in der Spalte und die Zeilen müssen gleich sein. Dieser Vorgang kann wie folgt dargestellt werden:

Slicing und Aggregation von Matrizen

Indizierungs- und Slicing-Funktionen werden bei der Bearbeitung von Matrizen nützlicher. Daten können mithilfe von Indexoperationen auf verschiedene Dimensionen aufgeteilt werden. Wir können Matrizen genauso aggregieren wie Vektoren: Wert, Sie können ihn auch mit dem Achsenparameter Aggregation von Zeilen und Spalten angeben:

Transposition und Rekonstruktion von Matrizen

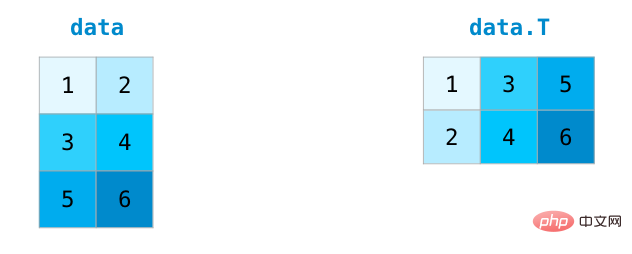
Bei der Verarbeitung von Matrizen ist es häufig erforderlich, die Matrix zu transponieren. Die Eigenschaft T eines NumPy-Arrays kann verwendet werden, um die Transponierte einer Matrix zu erhalten.

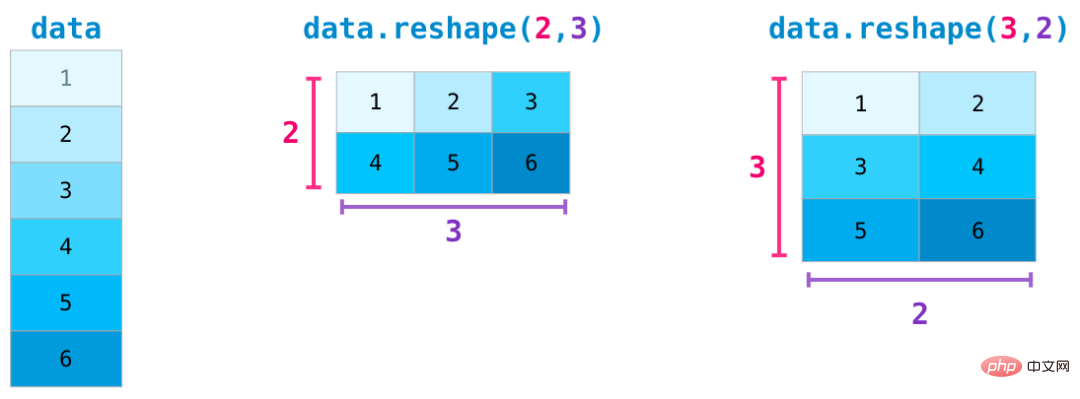
In komplexeren Anwendungsfällen müssen Sie möglicherweise die Abmessungen einer Matrix ändern. Dies ist bei maschinellen Lernanwendungen häufig der Fall. Wenn sich beispielsweise die Eingabematrixform des Modells vom Datensatz unterscheidet, können Sie die reshape()-Methode von NumPy verwenden. Übergeben Sie einfach die neuen Dimensionen, die für die Matrix erforderlich sind. Sie können auch -1 übergeben und NumPy kann anhand Ihrer Matrix auf die richtigen Dimensionen schließen:

Alle oben genannten Funktionen sind auf mehrdimensionale Daten anwendbar, und ihre zentrale Datenstruktur heißt ndarray (N-dimensionales Array).

Oft reicht es aus, die Dimension zu ändern, indem man dem Parameter der NumPy-Funktion ein Komma hinzufügt, wie unten gezeigt:

Beispiel für die Formelanwendung in NumPy

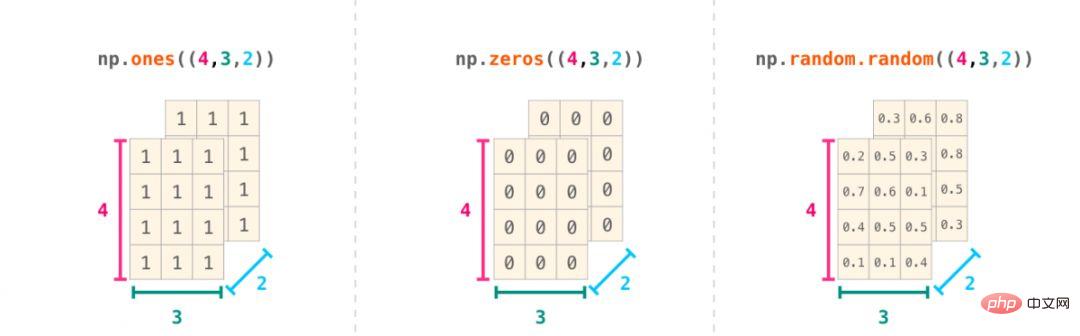
Ein wichtiger Anwendungsfall für NumPy ist die Implementierung mathematischer Formeln, die mit Matrizen und Vektoren arbeiten. Dies ist auch der Grund, warum NumPy häufig in Python verwendet wird. Beispielsweise ist der mittlere quadratische Fehler der Kern überwachter Modelle für maschinelles Lernen zur Behandlung von Regressionsproblemen:

Der mittlere quadratische Fehler kann einfach in NumPy implementiert werden:

Der Vorteil davon ist, dass Numpy die in Vorhersagen und Beschriftungen enthaltenen spezifischen Werte nicht berücksichtigen muss. DigestBacteria durchläuft die vier Operationen in der obigen Codezeile anhand eines Beispiels:

Sowohl die Vorhersage- als auch die Beschriftungsvektoren enthalten drei Werte. Das bedeutet, dass der Wert von n 3 ist. Nachdem wir die Subtraktion durchgeführt haben, erhalten wir Werte wie diesen:

Anschließend können wir das Quadrat jedes Werts im Vektor berechnen:

Jetzt summieren wir diese Werte:

, um schließlich den Fehlerwert und den Modellqualitätswert für diese Vorhersage zu erhalten.

Verwenden Sie NumPy, um tägliche Daten darzustellen

täglich Wie stellen Sie die Arten von Daten dar, mit denen Sie in Kontakt kommen, z. B. Tabellenkalkulationen, Bilder, Audio usw.? Numpy kann dieses Problem lösen.

Tabellen und Tabellenkalkulationen

Tabellen und Datenblätter sind beides zweidimensionale Matrizen. Jedes Arbeitsblatt in der Tabelle kann eine eigene Variable sein. Eine ähnliche Struktur in Python ist der Pandas-Datenrahmen, der tatsächlich mit NumPy erstellt wird.

Audio und Zeitreihen

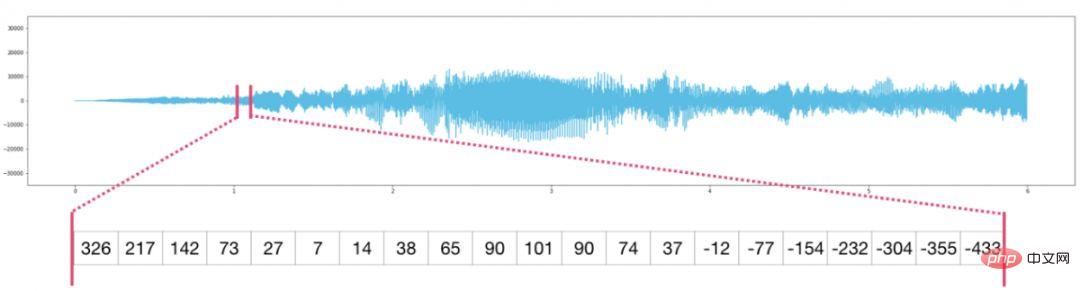
Audiodateien sind eindimensionale Arrays von Samples. Bei jedem Sample handelt es sich um eine Zahl, die einen kleinen Abschnitt des Audiosignals darstellt. Audio in CD-Qualität kann 44.100 Samples pro Sekunde haben, wobei jedes Sample eine Ganzzahl zwischen -65535 und 65536 ist. Das bedeutet, dass Sie eine 10 Sekunden lange WAVE-Datei in CD-Qualität in ein NumPy-Array mit der Länge 10 * 44.100 = 441.000 Samples laden können. Möchten Sie die erste Sekunde des Audios extrahieren? Laden Sie die Datei einfach in ein NumPy-Array, das wir „Audio“ nennen, und fangen Sie Audio ab[:44100].

Das Folgende ist eine Audiodatei:

Das Gleiche gilt für Zeitreihendaten (z. B. eine Abfolge von Aktienkursen im Zeitverlauf).

Bild

Ein Bild ist eine Pixelmatrix der Größe (Höhe × Breite). Wenn das Bild schwarzweiß ist (auch Graustufenbild genannt), kann jedes Pixel durch eine einzelne Zahl dargestellt werden (normalerweise zwischen 0 (schwarz) und 255 (weiß)). Wenn Sie ein Bild verarbeiten, können Sie mit image[:10,:10] in NumPy einen 10 x 10 Pixel großen Bereich in der oberen linken Ecke des Bildes zuschneiden.

Dies ist ein Ausschnitt einer Bilddatei:

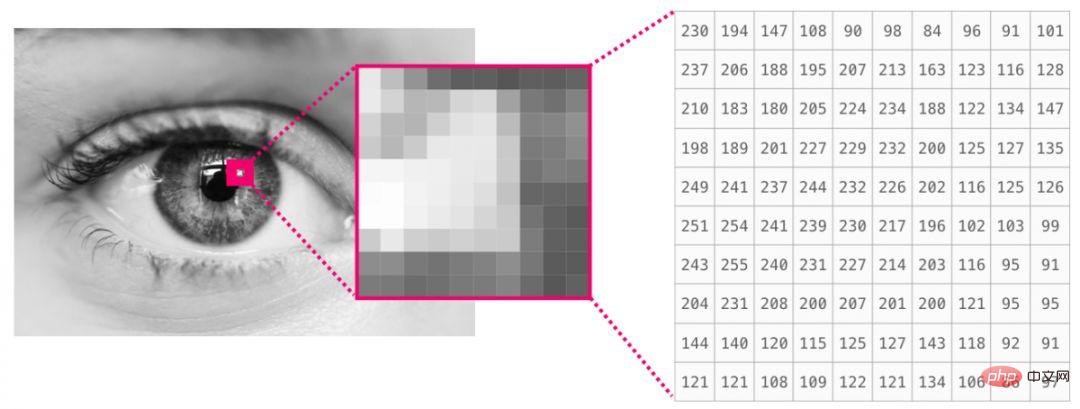
Wenn das Bild farbig ist, wird jedes Pixel durch drei Zahlen dargestellt: Rot, Grün und Blau. In diesem Fall benötigen wir eine dritte Dimension (da jede Zelle nur eine Zahl enthalten kann). Das Farbbild wird also durch ein Ndarray mit Abmessungen (Höhe x Breite x 3) dargestellt.

Sprache

Anders ist es, wenn wir uns mit Text befassen. Die numerische Darstellung von Text erfordert zwei Schritte: den Aufbau eines Vokabulars (eine Liste aller eindeutigen Wörter, die das Modell kennt) und die Einbettung. Schauen wir uns die Schritte an, um dieses (übersetzte) alte Zitat numerisch darzustellen: „Haben die Barden, die vor mir waren, ein Thema unbesungen gelassen?“

Das Modell muss an einer großen Textmenge trainiert werden, bevor es kann Zahlenmäßig stellen die Verse dieses Schlachtfelddichters dar. Wir können das Modell einen kleinen Datensatz verarbeiten lassen und diesen Datensatz verwenden, um ein Vokabular (71.290 Wörter) aufzubauen:

Der Satz kann dann in eine Reihe von „Wort“-Tokens (Wörter oder Wortteile basierend auf gemeinsamen Regeln) unterteilt werden:

Dann ersetzen wir jedes Wort durch seine ID aus dem Vokabular:

Diese IDs liefern dem Modell immer noch keine wertvollen Informationen. Bevor eine Folge von Wörtern in das Modell eingespeist wird, muss daher das Token/Wort durch eine Einbettung ersetzt werden (in diesem Fall durch eine 50-dimensionale Word2vec-Einbettung):

Sie können sehen, dass die Abmessungen dieses NumPy-Arrays [embedding_dimension x sequence_length] sind.

In der Praxis sehen diese Werte nicht unbedingt so aus, aber ich präsentiere sie aus Gründen der visuellen Konsistenz so. Aus Leistungsgründen neigen Deep-Learning-Modelle dazu, die erste Dimension der Batch-Größe beizubehalten (da das Modell schneller trainiert werden kann, wenn mehrere Beispiele parallel trainiert werden). Offensichtlich ist dies ein guter Ort, um reshape() zu verwenden. Beispielsweise würde ein Modell wie BERT erwarten, dass seine Eingabematrix die folgende Form hat: [Batch_size, sequence_length, embedding_size].

Dies ist eine Sammlung von Zahlen, die Modelle verarbeiten und verschiedene nützliche Operationen ausführen können. Ich habe viele Zeilen leer gelassen, die mit zusätzlichen Beispielen für das Modelltraining (oder die Vorhersage) ausgefüllt werden können.

Das obige ist der detaillierte Inhalt vonTipps |. Dies ist wahrscheinlich das beste grafische NumPy-Tutorial, das ich je gesehen habe!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!