 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 2)
Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 2)
Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 2)
Sortieralgorithmus Man kann sagen, dass jeder Programmierer es beherrschen muss Es ist notwendig, deren Prinzipien und Implementierung zu verstehen Das Folgende ist eine Einführung in die Python-Implementierung der zehn am häufigsten verwendeten Sortieralgorithmen, um Ihnen das Lernen zu erleichtern.
01 Blasensortierung – Austauschsortierung 02 Schnellsortierung – Austauschsortierung
03 Auswahlsortierung – Auswahlsortierung 04 Heapsortierung – Auswahlsortierung
05 Einfügungssortierung - Einfügungsklassensortierung
06 Hügelsortierung - Einfügungsklassensortierung
07 Zusammenführungssortierung - Zusammenführungsklassensortierung
08. Anzahl Sortierung - Verteilungssortierung 09 Radix-Sortierung – Verteilungssortierung 10 Bucket-Sortierung – Verteilungssortierung
und wiederholen Sie die obige Gruppierung und Sortierung
Wiederholen Sie den obigen Vorgang. Wenn Lücke = 1, endet die Sortierung
'''希尔排序'''
def Shell_Sort(arr):
# 设定步长,注意类型
step = int(len(arr) / 2)
while step > 0:
for i in range(step, len(arr)):
# 类似插入排序, 当前值与指定步长之前的值比较, 符合条件则交换位置
while i >= step and arr[i - step] > arr[i]:
arr[i], arr[i - step] = arr[i - step], arr[i]
i -= step
step = int(step / 2)
return arr
arr = [29, 63, 41, 5, 62, 66, 57, 34, 94, 22]
result = Shell_Sort(arr)
print('result list: ', result)
# result list: [5, 22, 29, 34, 41, 57, 62, 63, 66, 94]Platz so anlegen, dass seine Größe die Summe aus beiden ist Dieser Speicherplatz wird zum Speichern verwendet Die zusammengeführte Sequenz. Die Sequenz
legt zwei Indizes fest. Die anfänglichen Indexpositionen sind die Startpositionen der beiden sortierten Sequenzen
- Wählen Sie die relativ kleinen Elemente im Zusammenführungsbereich aus und verschieben Sie den
Index an die nächste Position
Wiederholen Sie den vorherigen Schritt, bis ein bestimmter Index - das Ende der Sequenz überschreitet
und entfernen Sie alle verbleibenden Elemente der anderen Sequenz. Elemente werden direkt an das Ende der zusammengeführten Sequenz kopiert
'''归并排序'''def Merge(left, right):
arr = []
i = j = 0
while j < len(left) and i < len(right):
if left[j] < right[i]:
arr.append(left[j])
j += 1
else:
arr.append(right[i])
i += 1
if j == len(left):
# right遍历完
for k in right[i:]:
arr.append(k)
else:
# left遍历完
for k in left[j:]:
arr.append(k)
return arr
def Merge_Sort(arr):
# 递归结束条件
if len(arr) <= 1:
return arr
# 二分
middle = len(arr) // 2
left = Merge_Sort(arr[:middle])
right = Merge_Sort(arr[middle:])
# 合并
return Merge(left, right)
arr = [27, 70, 34, 65, 9, 22, 47, 68, 21, 18]
result = Merge_Sort(arr)
print('result list: ', result)
# result list: [9, 18, 21, 22, 27, 34, 47, 65, 68, 70]找出待排序的数组中最大和最小的元素
统计数组中每个值为i的元素出现的次数,存入数组C的第i项
对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
'''计数排序'''
def Count_Sort(arr):
max_num = max(arr)
min_num = min(arr)
count_num = max_num - min_num + 1
count_arr = [0 for i in range(count_num)]
res = [0 for i in range(len(arr))]
# 统计数字出现的次数
for i in arr:
count_arr[i - min_num] += 1
# 统计前面有几个比自己小的数
for j in range(1, count_num):
count_arr[j] = count_arr[j] + count_arr[j - 1]
# 遍历重组
for k in range(len(arr)):
res[count_arr[arr[k] - min_num] - 1] = arr[k]
count_arr[arr[k] - min_num] -= 1
return res
arr = [5, 10, 76, 55, 13, 79, 5, 49, 51, 65, 30, 5]
result = Count_Sort(arr)
print('result list: ', result)
# result list: [5, 5, 5, 10, 13, 30, 49, 51, 55, 65, 76, 79]根据个位数的数值,遍历列表将它们分配至编号0到9的桶子中
将这些桶子中的数值重新串接起来
根据十位数的数值,遍历列表将它们分配至编号0到9的桶子中
再将这些桶子中的数值重新串接起来
'''基数排序'''
def Radix_Sort(arr):
max_num = max(arr)
place = 0
while 10 ** place <= max_num:
# 创建桶
buckets = [[] for _ in range(10)]
# 分桶
for item in arr:
pos = item // 10 ** place % 10
buckets[pos].append(item)
j = 0
for k in range(10):
for num in buckets[k]:
arr[j] = num
j += 1
place += 1
return arr
arr = [31, 80, 42, 47, 35, 26, 10, 5, 51, 53]
result = Radix_Sort(arr)
print('result list: ', result)
# result list: [5, 10, 26, 31, 35, 42, 47, 51, 53, 80]计算有限桶的数量
逐个桶内部排序
遍历每个桶,进行合并
'''桶排序'''
def Bucket_Sort(arr):
num = max(arr)
# 列表置零
pre_lst = [0] * num
result = []
for data in arr:
pre_lst[data - 1] += 1
i = 0
while i < len(pre_lst): # 遍历生成的列表,从小到大
j = 0
while j < pre_lst[i]:
result.append(i + 1)
j += 1
i += 1
return result
arr = [26, 53, 83, 86, 5, 46, 5, 72, 21, 4, 75]
result = Bucket_Sort(arr)
print('result list: ', result)
# result list: [4, 5, 5, 21, 26, 46, 53, 72, 75, 83, 86]Das obige ist der detaillierte Inhalt vonDie zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 2). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Komplexe experimentelle Designprobleme im zweiseitigen Markt von Kuaishou
Apr 15, 2023 pm 07:40 PM
Komplexe experimentelle Designprobleme im zweiseitigen Markt von Kuaishou
Apr 15, 2023 pm 07:40 PM
1. Hintergrund des Problems 1. Einführung in das zweiseitige Marktexperiment Der zweiseitige Markt, also eine Plattform, umfasst zwei Teilnehmer, Produzenten und Verbraucher, und beide Parteien fördern sich gegenseitig. Kuaishou hat beispielsweise einen Videoproduzenten und einen Videokonsumenten, und die beiden Identitäten können sich bis zu einem gewissen Grad überschneiden. Bilaterales Experiment ist eine experimentelle Methode, die Gruppen auf Produzenten- und Verbraucherseite vereint. Bilaterale Experimente haben folgende Vorteile: (1) Die Auswirkungen der neuen Strategie auf zwei Aspekte können gleichzeitig erfasst werden, beispielsweise Änderungen im Produkt-DAU und die Anzahl der Personen, die Werke hochladen. Bilaterale Plattformen haben oft netzwerkübergreifende Effekte, je mehr Leser es gibt, desto aktiver werden die Autoren sein, und je aktiver die Autoren sind, desto mehr Leser werden ihnen folgen. (2) Effektüberlauf und -übertragung können erkannt werden. (3) Helfen Sie uns, den Wirkungsmechanismus besser zu verstehen. Das AB-Experiment selbst kann uns nicht nur den Zusammenhang zwischen Ursache und Wirkung aufzeigen
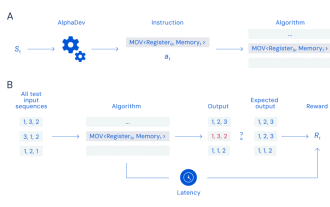 Google nutzt KI, um das Zehn-Jahres-Ranking-Algorithmus-Siegel zu brechen. Es wird jeden Tag Billionen Mal ausgeführt, aber Internetnutzer sagen, es sei die unrealistischste Forschung?
Jun 22, 2023 pm 09:18 PM
Google nutzt KI, um das Zehn-Jahres-Ranking-Algorithmus-Siegel zu brechen. Es wird jeden Tag Billionen Mal ausgeführt, aber Internetnutzer sagen, es sei die unrealistischste Forschung?
Jun 22, 2023 pm 09:18 PM
Organisieren |. Nuka-Cola, Chu Es ist eine interessante Herausforderung und es gibt viele Möglichkeiten, sie zu meistern. Es wurde viel Zeit investiert, um herauszufinden, wie Sortieraufgaben effizienter erledigt werden können. Als Grundoperation sind Sortieralgorithmen in die Standardbibliotheken der meisten Programmiersprachen integriert. Es gibt viele verschiedene Sortiertechniken und Algorithmen, die in Codebasen auf der ganzen Welt verwendet werden, um große Datenmengen online zu organisieren, aber zumindest was die mit dem LLVM-Compiler verwendeten C++-Bibliotheken betrifft, hat sich der Sortiercode seit mehr als einem Jahr nicht geändert Jahrzehnt. Kürzlich hat das Google DeepMindAI-Team nun eine entwickelt
 So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung
Oct 09, 2023 pm 01:25 PM
So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung
Oct 09, 2023 pm 01:25 PM
So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung. In der Vue-Technologieentwicklung sind das Filtern und Sortieren von Daten sehr häufige und wichtige Funktionen. Durch Datenfilterung und -sortierung können wir die benötigten Informationen schnell abfragen und anzeigen und so die Benutzererfahrung verbessern. In diesem Artikel wird das Filtern und Sortieren von Daten in Vue vorgestellt und spezifische Codebeispiele bereitgestellt, um den Lesern zu helfen, diese Funktionen besser zu verstehen und zu verwenden. 1. Datenfilterung Datenfilterung bezieht sich auf das Herausfiltern von Daten, die den Anforderungen basierend auf bestimmten Bedingungen entsprechen. In Vue können wir comp bestehen
 Welche Sortieralgorithmen gibt es für Arrays?
Jun 02, 2024 pm 10:33 PM
Welche Sortieralgorithmen gibt es für Arrays?
Jun 02, 2024 pm 10:33 PM
Array-Sortieralgorithmen werden verwendet, um Elemente in einer bestimmten Reihenfolge anzuordnen. Zu den gängigen Arten von Algorithmen gehören: Blasensortierung: Vertauschen Sie Positionen durch Vergleichen benachbarter Elemente. Auswahlsortierung: Finden Sie das kleinste Element und tauschen Sie es an die aktuelle Position aus. Einfügungssortierung: Elemente einzeln an der richtigen Position einfügen. Schnelle Sortierung: Divide-and-Conquer-Methode, wählen Sie das Pivot-Element aus, um das Array zu teilen. Zusammenführungssortierung: Teilen und Erobern, rekursives Sortieren und Zusammenführen von Unterarrays.
 So implementieren Sie eine einfache Sortieralgorithmusfunktion mit MySQL und Java
Sep 20, 2023 am 09:45 AM
So implementieren Sie eine einfache Sortieralgorithmusfunktion mit MySQL und Java
Sep 20, 2023 am 09:45 AM
So implementieren Sie mit MySQL und Java eine einfache Sortieralgorithmusfunktion. Einführung: In der Softwareentwicklung gehören Sortieralgorithmen zu den grundlegendsten und am häufigsten verwendeten Funktionen. In diesem Artikel wird erläutert, wie Sie mithilfe von MySQL und Java eine einfache Sortieralgorithmusfunktion implementieren, und es werden spezifische Codebeispiele bereitgestellt. 1. Übersicht über Sortieralgorithmen Sortieralgorithmen sind Algorithmen, die einen Datensatz nach bestimmten Regeln anordnen. Zu den häufig verwendeten Sortieralgorithmen gehören Blasensortierung, Einfügungssortierung, Auswahlsortierung, Schnellsortierung usw. In diesem Artikel wird die Blasensortierung als Beispiel zur Erläuterung und Implementierung verwendet. 2. M
 Swoole Advanced: So verwenden Sie Multithreading, um einen Hochgeschwindigkeits-Sortieralgorithmus zu implementieren
Jun 14, 2023 pm 09:16 PM
Swoole Advanced: So verwenden Sie Multithreading, um einen Hochgeschwindigkeits-Sortieralgorithmus zu implementieren
Jun 14, 2023 pm 09:16 PM
Swoole ist ein leistungsstarkes Netzwerkkommunikations-Framework, das auf der PHP-Sprache basiert. Es unterstützt die Implementierung mehrerer asynchroner E/A-Modi und mehrerer erweiterter Netzwerkprotokolle. Basierend auf Swoole können wir seine Multithreading-Funktion nutzen, um effiziente Algorithmusoperationen zu implementieren, beispielsweise Hochgeschwindigkeits-Sortieralgorithmen. Der Hochgeschwindigkeits-Sortieralgorithmus (QuickSort) ist ein gängiger Sortieralgorithmus. Durch die Lokalisierung eines Benchmark-Elements werden die Elemente, die kleiner als das Benchmark-Element sind, auf der linken Seite platziert, und diejenigen, die größer oder gleich dem Benchmark sind Element werden auf der rechten Seite platziert. Dann werden die linke und die rechte Teilsequenzrekursion platziert
 So implementieren Sie den Auswahlsortierungsalgorithmus in C#
Sep 20, 2023 pm 01:33 PM
So implementieren Sie den Auswahlsortierungsalgorithmus in C#
Sep 20, 2023 pm 01:33 PM
So implementieren Sie den Auswahlsortierungsalgorithmus in C#. Die Auswahlsortierung (SelectionSort) ist ein einfacher und intuitiver Sortieralgorithmus. Seine Grundidee besteht darin, jedes Mal das kleinste (oder größte) Element aus den zu sortierenden Elementen auszuwählen und am Ende einzufügen die sortierte Reihenfolge. Wiederholen Sie diesen Vorgang, bis alle Elemente sortiert sind. Erfahren Sie mehr darüber, wie Sie den Auswahlsortierungsalgorithmus in C# implementieren, zusammen mit spezifischen Codebeispielen. Erstellen einer Auswahlsortierungsmethode Zuerst müssen wir eine Methode zur Implementierung der Auswahlsortierung erstellen. Diese Methode akzeptiert a
 Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 1)
Aug 15, 2023 pm 02:55 PM
Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 1)
Aug 15, 2023 pm 02:55 PM
Man kann sagen, dass Sortieralgorithmen etwas sind, das jeder Programmierer beherrschen muss. Um Ihnen das Lernen zu erleichtern, finden Sie im Folgenden eine Einführung in die Python-Implementierung.





