
Ein Quadrat ist eine zweidimensionale Form mit vier gleich langen Seiten. Gegenüberliegende Seiten eines Quadrats sind parallel, alle vier Innenwinkel sind rechte Winkel und die Diagonalen sind gleich lang. In diesem Artikel untersuchen wir, wie wir bestätigen können, ob bestimmte vier Punkte ein Quadrat bilden.
Wir erhalten ein Quadrat mit vier Punkten, nämlich A, B, C, D, wie im Bild gezeigt −
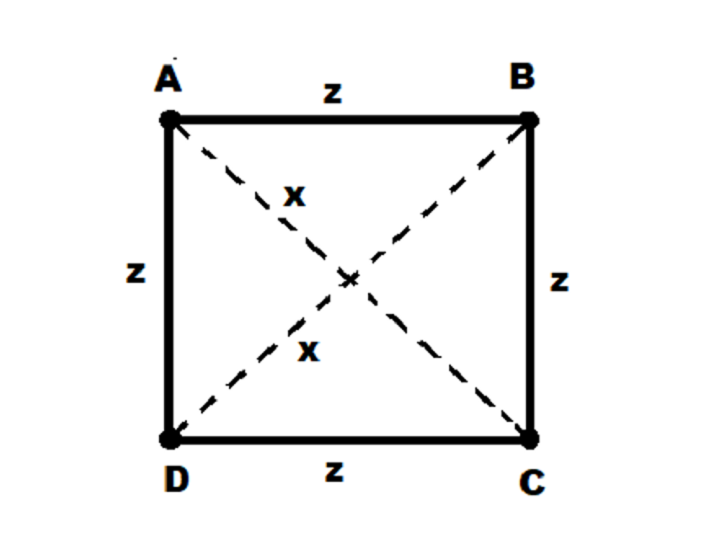
Anhand dieser Punkte müssen wir prüfen, ob sie ein Quadrat bilden. Um dies zu überprüfen, sollte es die folgenden Bedingungen erfüllen: −
Der Abstand zwischen Punkt A und Punkt C und der Abstand zwischen Punkt B und Punkt D, d. h. „x“, sollten gleich sein.
Der Abstand zwischen Punkt A und Punkt B, der Abstand zwischen Punkt B und Punkt C, der Abstand zwischen Punkt C und Punkt D, der Abstand zwischen Punkt D und Punkt A, d. h. „z“ sollte gleich sein.
Wir ermitteln den Abstand zwischen zwei Punkten mithilfe der Formel -
$$mathrm{d=sqrt{(x_{2}-x_{1})^2(y_{2}-y_{1})^2}}$$
Punkt 1 wird (x1, y1) sein und Punkt 2 wird (x2, y2) sein.
Lass uns anfangen!
Gegeben sind vier Eingabepunkte: -
P1(3,7), P2(4,3), P3(7,8), P4(1,9)
Setzen Sie es in die Abstandsformel ein und prüfen Sie, ob die Quadratbedingung erfüllt ist. Das Ergebnis ist -
Gegebene vier Punkte bilden kein Quadrat.
Gegeben sind vier Eingabepunkte: -
P1(20,20), P2(20,10), P3(10,10), P4(10,20)
Setzen Sie es in die Abstandsformel ein und prüfen Sie, ob die Quadratbedingung erfüllt ist. Das Ergebnis ist -
Gegeben sind vier Punkte, die ein Quadrat bilden.
Schritt 1 − Variablen deklarieren und initialisieren.
Schritt 2 − Ermitteln Sie den Abstand zwischen Mittelpunkt 1 und Mittelpunkt 2 des Kreises.
Schritt 3 – Überprüfen Sie die fünf Abstandsbedingungen.
Schritt 4 − Drucken Sie das Ergebnis aus.
Wir bieten Lösungen auf unterschiedliche Weise.
Durch die Verwendung statischer Eingaben
Durch die Verwendung benutzerdefinierter Methoden
Schauen wir uns das Programm und seine Ausgabe einzeln an.
Bei dieser Methode werden Punktwerte zugewiesen. Dann werden wir anhand des Algorithmus herausfinden, ob die gegebenen vier Punkte ein Quadrat bilden.
Die chinesische Übersetzung vonpublic class Main{
//main method
public static void main(String[] args){
//declaring variables
int x1=3, x2=4, x3=7, x4=1;
int y1=7, y2=3, y3=8, y4=9;
double d1, d2, d3, d4, d5, d6;
//applyinng logic
d1 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
d2 = (x3 - x2) * (x3 - x2) + (y3 - y2) * (y3 - y2);
d3 = (x4 - x3) * (x4 - x3) + (y4 - y3) * (y4 - y3);
d4 = (x1 - x4) * (x1 - x4) + (y1 - y4) * (y1 - y4);
d5 = (x4 - x2) * (x4 - x2) + (y4 - y2) * (y4 - y2);
d6 = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1);
if (d1 == 0 || d2 == 0 || d3 == 0 || d4 == 0 || d5 == 0 || d6 == 0){
System.out.println("Given four points do not form a square");
}
else if (d1 == d2 && d2 == d3 && d3 == d4 && d5 == d6){
//prints if four points form square
System.out.println("Given four points form a square");
} else {
//prints if four points do not form square
System.out.println("Given four points do not form a square");
}
}
}
Given four points do not form a square
Bei dieser Methode werden Punktwerte zugewiesen. Anschließend wird eine benutzerdefinierte Methode aufgerufen, die den angegebenen Wert übergibt und anhand des Algorithmus ermittelt, ob die angegebenen vier Punkte ein Quadrat bilden.
Die chinesische Übersetzung vonpublic class Main{
//main method
public static void main(String[] args){
//creating objects of Point
Point p1 = new Point(20, 20);
Point p2 = new Point( 20, 10 );
Point p3 = new Point(10, 10 );
Point p4 = new Point( 10, 20 );
//calling user defined method
if(isSquare(p1, p2, p3, p4)==true){
//print if four points form a square
System.out.println("Given four points form a square");
}
else{
//print if points does not form a square
System.out.println("Given four points do not form a square");
}
}
// Declaring Point class
static class Point{
int x, y;
public Point(int x, int y){
this.x = x;
this.y = y;
}
};
//function to find square of distance from point 'p' to point 'q'
static int distSq(Point p, Point q){
return (p.x - q.x) * (p.x - q.x) + (p.y - q.y) * (p.y - q.y);
}
//user defined method
static boolean isSquare(Point p1, Point p2, Point p3, Point p4){
int d1 = distSq(p1, p2);
int d2 = distSq(p2, p3);
int d3 = distSq(p3, p4);
int d4 = distSq(p4, p1);
int d5 = distSq(p1, p3);
int d6 = distSq(p2, p4);
if (d1 == 0 || d2 == 0 || d3 == 0 || d4 == 0 || d5 == 0 || d6 == 0)
return false;
if (d1 == d2 && d2 == d3 && d3 == d4 && d5 == d6){
//it returns true if (p1, p2, p3, p4) form a square
return true;
}
//it returns false if (p1, p2, p3, p4) do not form a square
return false;
}
}
Given four points form a square
In diesem Artikel untersuchen wir verschiedene Möglichkeiten, mithilfe der Programmiersprache Java zu überprüfen, ob eine Linie einen Kreis berührt, schneidet oder außerhalb liegt.
Das obige ist der detaillierte Inhalt vonWie kann man in Java bestätigen, ob gegebene vier Punkte ein Quadrat bilden?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!