Binärbaum ist eine faszinierende Datenstruktur mit einem breiten Anwendungsspektrum in der Informatik und Programmierung. Ein interessantes Problem besteht darin, die Anzahl eines gegebenen Baums zu ermitteln, der aus einem übergeordneten Knoten und seinen untergeordneten Knoten besteht. Ein Binärbaum besteht aus Knoten, der Wurzelknoten wird bestimmt und der Wurzelknoten kann entsprechend den Benutzeranforderungen untergeordnete Knoten bereitstellen. Der K-Wert wird bestimmt und die Bewegungsmethode wird durch den M-Wert ausgewählt.
Das Diagramm wird mithilfe verschiedener Knoten erstellt, die Werte in Form von Ganzzahlen enthalten. Dieser Artikel konzentriert sich hauptsächlich auf das Zählen vom Startknoten oder Wurzelknoten bis zum Blattknoten oder untergeordneten Knoten.
Der Graph wird aus einem Binärbaum mit verschiedenen Knoten erstellt.
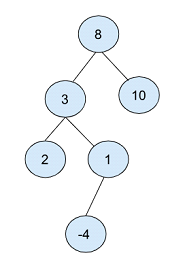
Im obigen Binärbaum wird der Wurzelknoten als „8“ ausgewählt.
Dann erstellen Sie zwei Knoten, einen mit dem Wert 3 und den anderen mit dem Wert 10, die die linke und rechte Position des Wurzelknotens einnehmen.
Nehmen Sie den Knoten mit dem Wert 2 als Wurzel und erstellen Sie einen weiteren untergeordneten Knoten mit den Werten 2 und 1 als linken bzw. rechten Knoten.
Schließlich erstellt der untergeordnete Knoten mit dem Wert 1 einen untergeordneten Knoten mit dem Wert -4.
Um dieses Problem effizient zu lösen, verwenden wir grundlegende Konzepte wie den Baumdurchquerungsalgorithmus und die Rekursion.
Schritt 1: Erstellen Sie eine Struktur zur Darstellung des Baumknotens, die zwei Zeiger (linker untergeordneter Knoten und rechter untergeordneter Knoten) und ein Ganzzahlfeld zum Speichern des Knotenwerts enthält.
Schritt 2: Entwerfen Sie eine rekursive Funktion, um den Binärbaum ausgehend von der Wurzel zu durchlaufen und dabei die aktuelle Pfadlänge (initialisiert auf 0), die Anzahl aufeinanderfolgender Vorkommen (ursprünglich auf 0 gesetzt), den Zielwert K usw. zu verfolgen die maximal zulässige Anzahl aufeinanderfolgender Vorkommen M .
Schritt 3: Rufen Sie die Funktion rekursiv für jeden linken und rechten Teilbaum auf und übergeben Sie dabei aktualisierte Parameter wie die inkrementelle Pfadlänge und die Anzahl aufeinanderfolgender Vorkommen (falls zutreffend).
Schritt 4: Für jeden nicht leeren Knoten, der während der Durchquerung besucht wird:
a) Wenn sein Wert gleich K ist, addieren Sie eins zu beiden Variablen.
b) Setzen Sie die Variable auf Null zurück, wenn ihr Wert nicht mit K übereinstimmt oder die Anzahl der aufeinanderfolgenden Vorkommen von M überschreitet, die bisher im Pfad aufgetreten sind.
Schritt 5: Wenn der untergeordnete Knoten beim Durchlaufen des Baums sowohl im linken als auch im rechten Fall einen Wert von Null hat, können wir auf zwei Arten damit umgehen, d. h.
a) Überprüfen Sie, ob die Variable M nicht überschreitet.
b) Wenn ja, erhöhen Sie die Gesamtzahl der Pfade, die die Bedingung erfüllen, um 1.
//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
if (end == NULL || consCount > M) {
return 0;
}
//To check when the root is equal to the K value, increment by 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//If it is not equal, it will return 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // Value of node
int M = 2; // Maximum consecutive nodes
int currCount = -1; // Current count
int consCount = -1; // Consecutive count
cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3
In diesem Artikel untersuchen wir das Problem der Zählung der Anzahl der Pfade von der Spitze (d. h. dem Blatt) bis zur Spitze oder Wurzel. Solche Probleme können durch den Einsatz von Baumdurchlaufalgorithmen und rekursiven Techniken in C++ effizient gelöst werden. Das Durchlaufen eines Binärbaums mag schwierig erscheinen, anhand von Beispielen wird es jedoch einfacher.
Das obige ist der detaillierte Inhalt vonAnzahl der Pfade von der Wurzel zu den Blättern mit höchstens M aufeinanderfolgenden Knoten und dem Wert K. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
