Ermitteln Sie in der C-Programmierung die Fläche eines Kreises

Ein Kreis ist eine geschlossene Form. Alle Punkte auf einem Kreis haben den gleichen Abstand von einem Punkt innerhalb des Kreises. Der Mittelpunkt wird Kreismittelpunkt genannt. Der Abstand von einem Punkt zum Mittelpunkt eines Kreises wird Radius genannt.
Fläche ist eine quantitative Darstellung der Größenspanne einer geschlossenen Figur.
Die Fläche eines Kreises ist die Fläche, die von den Abmessungen des Kreises umschlossen wird.
Formel zur Berechnung der Fläche eines Kreises,
Area = π*r*r
Zur Berechnung der Fläche erhalten wir den Radius des Kreises als Eingabe. Wir verwenden die Formel zur Berechnung der Fläche,
Algorithmus
STEP 1: Take radius as input from the user using std input. STEP 2: Calculate the area of circle using, area = (3.14)*r*r STEP 3: Print the area to the screen using the std output.
Beispiel
Variablen verwendet -
int r , der Radius eines Kreises
float area, die Fläche eines Kreises, berechnet nach der Formel.
Live-Demonstration
#include <stdio.h>
int main(){
int r = 8;
float area = (3.14)*r*r;
printf("The area of the circle is %f",area);
return 0;
}Ausgabe
The area of the circle is 200.96
Das obige ist der detaillierte Inhalt vonErmitteln Sie in der C-Programmierung die Fläche eines Kreises. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
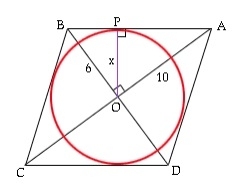 Wie groß ist die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 05, 2023 am 08:25 AM
Wie groß ist die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 05, 2023 am 08:25 AM
Der eingeschriebene Kreis einer Raute tangiert ihre vier Seiten und vier Endpunkte. Die Seiten der Raute berühren den Kreis. Hier ist r der Radius, der mithilfe von a und der Diagonale des angegebenen Werts ermittelt wird. Nun ist das Flächendreieck AOB = ½*OA*OB = ½*AB*r (beide verwenden die Formel ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Kreisfläche = π*r*r=π*(a2*b2)/4(a2support>+b2) Beispiel für die Diagonalen der Raute 5 und 10. Die Fläche beträgt 15,700000. Beispielcode. Echtzeitdemonstration #include<stdio.h>intma
 So markieren Sie den Bereich im CAD
Mar 14, 2023 am 11:30 AM
So markieren Sie den Bereich im CAD
Mar 14, 2023 am 11:30 AM
Methode zur Bereichsbeschriftung in CAD: 1. Öffnen Sie CAD, klicken Sie auf „Zeichnen“, um Grafiken zu zeichnen. 2. Geben Sie den Befehl „BEREICH“ ein und drücken Sie die Eingabetaste. 3. Drücken Sie die Leertaste, um den Bereich anzuzeigen die Fläche; 5. Geben Sie den Befehl „T“ ein und geben Sie dann die Größe der Fläche innerhalb der Fläche ein.
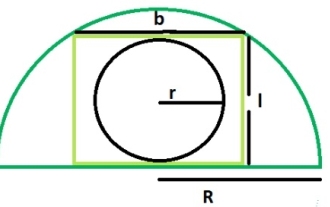 Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 13, 2023 am 08:45 AM
Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 13, 2023 am 08:45 AM
Ein in ein Rechteck eingeschriebener Kreis tangiert die längere Seite des Rechtecks, d. h. seine Länge tangiert den Kreis. Ein in einen Halbkreis eingeschriebenes Rechteck berührt zwei Punkte auf dem Bogen des Halbkreises. Die Breite des Rechtecks entspricht dem Durchmesser des Kreises. Wenn R der Radius des Halbkreises ist. Die Länge des Rechtecks = √2R/2 Die Breite des Rechtecks = R/√2 Der Radius des eingeschriebenen Kreises beträgt r = b/2 = R/2√2 Mit dieser Formel können wir das in den Halbkreis eingeschriebene Rechteck berechnen Die Fläche eines Kreises, Fläche = (π*r2)=π*R/8 Beispieldemonstration #include<stdio.h>intmain(){&
 Wie groß ist die Fläche des Kreissektors?
Aug 30, 2023 am 08:33 AM
Wie groß ist die Fläche des Kreissektors?
Aug 30, 2023 am 08:33 AM
Ein Kreissektor, auch Kreissektor/Kreissektor genannt, ist ein Teil eines Kreises, der durch einen Bogen zwischen zwei Radien begrenzt wird. Dieser Bereich wird durch zwei Radien und einen Bogen begrenzt. Um die eingeschriebene Fläche zu finden, müssen wir den Winkel zwischen den beiden Radien ermitteln. Die Gesamtfläche entspricht einem Winkel von 360 Grad. Um die Fläche eines Winkels zu ermitteln, multiplizieren wir die Fläche mit θ/360. Dies ergibt die Fläche des beschrifteten Teils. Dabei ist θ der Winkel (in Grad) zwischen den beiden Radien. Die Fläche des Kreissektors = π*r*r*(θ/360). Beispielsweise beträgt die Fläche eines Kreissektors mit einem Radius von 5 und einem Winkel von 60 Grad 13,083. Fläche=(3,14*5*5)*(60/360)=13,03BeispielcodeDemo#inkl
 So messen Sie die Fläche von Grafiken im CAD Viewer. So messen Sie die Fläche von Grafiken im CAD Viewer.
Mar 13, 2024 pm 01:43 PM
So messen Sie die Fläche von Grafiken im CAD Viewer. So messen Sie die Fläche von Grafiken im CAD Viewer.
Mar 13, 2024 pm 01:43 PM
Wie misst man die Fläche von Grafiken im CAD Viewer? CAD Viewer ist eine sehr benutzerfreundliche Software zum Anzeigen von Konstruktionszeichnungen. Diese Software verfügt über viele Funktionen und Zeichnungen in verschiedenen Formaten können geöffnet und angezeigt werden. Wenn wir beim Betrachten der Zeichnungen feststellen, dass die Flächenmessung einiger Grafiken falsch ist oder dass einige Grafiken vergessen haben, die Fläche zu messen, können wir diese Software verwenden, um die Fläche der Grafiken zu messen. Wie misst man also die Fläche einer Grafik? Im Folgenden hat der Herausgeber dieser Website die Schritte eines CAD-Zeichnungskönigs zum Messen der Fläche einer Grafik als Referenz zusammengestellt. Schritte zum Messen der Grafikfläche im CAD Viewer 1. Öffnen Sie zunächst die Zeichnungsdatei in der CAD Viewer-APP, nehmen Sie die Zeichnung mit Bogengrafiken als Beispiel und messen Sie die Grafikfläche. 2. Gehen Sie nach dem Öffnen der Zeichnung zum unteren Rand der Softwareoberfläche
 Verwenden Sie C++, um Code zu schreiben, um die N-te nichtquadratische Zahl zu finden
Aug 30, 2023 pm 10:41 PM
Verwenden Sie C++, um Code zu schreiben, um die N-te nichtquadratische Zahl zu finden
Aug 30, 2023 pm 10:41 PM
Wir alle kennen Zahlen, die nicht das Quadrat einer Zahl sind, wie zum Beispiel 2, 3, 5, 7, 8 usw. Es gibt N nichtquadratische Zahlen und es ist unmöglich, jede Zahl zu kennen. In diesem Artikel erklären wir alles über quadratlose oder nichtquadratische Zahlen und Möglichkeiten, die N-te nichtquadratische Zahl in C++ zu finden. N-te nichtquadratische Zahl Wenn eine Zahl das Quadrat einer ganzen Zahl ist, wird die Zahl als perfektes Quadrat bezeichnet. Einige Beispiele für perfekte Quadratzahlen sind -1isquadratvon14isquadratvon29isquadratvon316isquadratvon425isquadratvon5. Wenn eine Zahl nicht das Quadrat einer ganzen Zahl ist, wird die Zahl als nichtquadratisch bezeichnet. Die ersten 15 nichtquadratischen Zahlen sind beispielsweise -2,3,5,6,
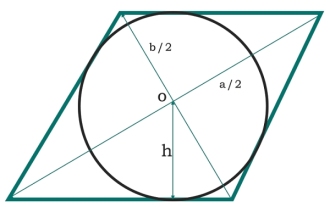 Wie groß ist im C-Programm die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 01, 2023 pm 09:29 PM
Wie groß ist im C-Programm die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 01, 2023 pm 09:29 PM
Hier sehen wir die Fläche eines Kreises, der in eine Raute eingeschrieben ist. Die Diagonalen der Raute sind „a“ bzw. „b“. Der Radius des Kreises beträgt h. Zwei Diagonalen bilden vier gleiche Dreiecke. Jedes Dreieck ist ein rechtwinkliges Dreieck, also ist ihre Fläche - Jede Seite der Raute ist die Hypotenuse - Daher ist die Fläche des Kreises - Beispiel#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb ) { if(a<0||b<0)//ifthevaluesaren
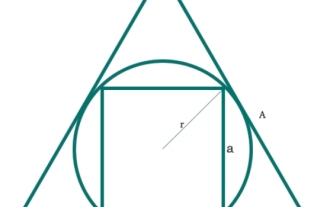 Übersetzen Sie in einem C-Programm Folgendes ins Chinesische: Wie groß ist die Fläche eines Quadrats, das in einen Kreis eingeschrieben ist, der in ein gleichseitiges Dreieck eingeschrieben ist?
Aug 31, 2023 pm 12:25 PM
Übersetzen Sie in einem C-Programm Folgendes ins Chinesische: Wie groß ist die Fläche eines Quadrats, das in einen Kreis eingeschrieben ist, der in ein gleichseitiges Dreieck eingeschrieben ist?
Aug 31, 2023 pm 12:25 PM
Hier sehen wir, dass die Fläche eines Quadrats in einen Kreis eingeschrieben ist und dass der Kreis in ein gleichseitiges Dreieck eingeschrieben ist. Die Seite des Quadrats ist „a“. Der Radius des Kreises ist „r“ und die Seite des Sechsecks ist „A“. Das Diagramm ist unten dargestellt. Die Diagonale des Quadrats ist also – also die Fläche des Quadrats – Beispiel #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne




