Finden Sie alle möglichen Koordinaten eines Parallelogramms in Java
Ein Parallelogramm ist ein Viereck mit zwei Paaren paralleler Seiten, wobei gegenüberliegende Seiten gleich lang und Diagonalen gleich groß sind.
In diesem Artikel werden wir alle möglichen Koordinaten eines Parallelogramms finden.
Grundsätzlich ermitteln wir alle möglichen Koordinaten aus den angegebenen drei Koordinaten, um ein Parallelogramm einer Fläche ungleich Null zu erstellen. Dabei sind die drei angegebenen Koordinaten keine Fixpunkte und können sich ändern.
Wenn also drei Koordinaten angegeben sind, können wir behaupten, dass nur diese drei Koordinaten ein Parallelogramm konstruieren können.
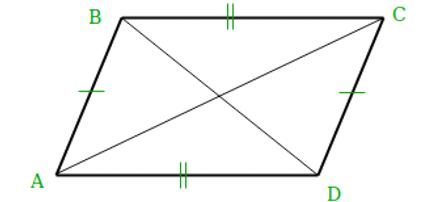
Gemäß dem oben angegebenen Diagramm sind die gegenüberliegenden Seiten eines Parallelogramms gleich lang, d. h. AD = BC und AB = CD. Wir können die Koordinaten des fehlenden Punkts (D) berechnen als
AD = BC
(Dx – Ax, Dy – Ay) = (Cx – Bx, Cy – By)
Dx = Ax + Cx - Bx
Dy = Ay + Cy - By
Lass uns anfangen!
Zeigen Sie einige Beispiele
Instanz-1
Angenommen, diese drei Punkte sind −
{a1 = 3, a2 = 2}, {b1 = 1, b2 = 0}, {c1 = 4, c2 = 2}
Nachdem alle möglichen Koordinaten eines Parallelogramms gefunden wurden, lautet das Ergebnis −
Die (x, y)-Koordinaten sind −
0, 0
6, 4
2, 0
Instanz-2
Angenommen, diese drei Punkte sind −
{a1 = 7, a2 = 2}, {b1 = 3, b2 = 0}, {c1 =0, c2 = 1}
Nachdem alle möglichen Koordinaten eines Parallelogramms gefunden wurden, lautet das Ergebnis −
Die (x,y)-Koordinaten sind −
10, 1
4, 3
-4, -1
Algorithmus
Schritt 1 − Deklarieren Sie die drei Koordinaten des Parallelogramms.
Schritt 2 − Finden Sie die anderen möglichen Koordinaten mithilfe der Formel.
Schritt 3 − Drucken Sie das Ergebnis aus.
Mehrere Ansätze
Wir bieten Lösungen auf unterschiedliche Weise.
Durch Verwendung statischer Eingabewerte
über benutzerdefinierte Methoden
Schauen wir uns das Programm und seine Ausgabe einzeln an.
Methode 1: Durch Verwendung statischer Eingabewerte
Bei dieser Methode nehmen wir diese drei Punkte als statische Eingabe und wenden die Formel an, um das Ergebnis auszudrucken.
Beispiel
public class Main{
// main method
public static void main(String[] args){
//Declare the three coordinates of parallelogram
int a1 = 3, a2 = 2;
int b1 = 1, b2 = 0;
int c1 = 4, c2 = 2;
//find the other possible coordinates and printing it
System.out.println("The (x,y) coordinates are: ");
System.out.println(a1 + b1 - c1 + ", " + (a2 + b2 - c2));
System.out.println(a1 + c1 - b1 + ", " + (a2 + c2 - b2));
System.out.println(c1 + b1 - a1 + ", " + (c2 + b2 - a2));
}
}
Ausgabe
The (x,y) coordinates are: 0, 0 6, 4 2, 0
Ansatz 2: Durch Verwendung einer benutzerdefinierten Methode
Bei diesem Ansatz initialisieren wir zunächst eine benutzerdefinierte Methode, nehmen die drei Punkte als Eingabe und wenden die Formel an, um das Ergebnis zu drucken.
Beispiel
public class Main {
// main method
public static void main(String[] s){
//Declare the three coordinates of parallelogram
int a1 = 7, a2 = 2;
int b1 = 3, b2 = 0;
int c1 = 0, c2 = 1;
//calling user defined function
func(a1, a2, b1, b2, c1, c2);
}
//user defined function
static void func(int a1, int a2, int b1, int b2, int c1, int c2){
//find the other possible coordinates and printing it
System.out.println("The (x,y) coordinates are: ");
System.out.println(a1 + b1 - c1 + ", " + (a2 + b2 - c2));
System.out.println(a1 + c1 - b1 + ", " + (a2 + c2 - b2));
System.out.println(c1 + b1 - a1 + ", " + (c2 + b2 - a2));
}
}
Ausgabe
The (x,y) coordinates are: 10, 1 4, 3 -4, -1
In diesem Artikel haben wir untersucht, wie man mit verschiedenen Methoden alle möglichen Koordinaten eines Parallelogramms in Java findet.
Das obige ist der detaillierte Inhalt vonFinden Sie alle möglichen Koordinaten eines Parallelogramms in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur Smith-Zahl in Java. Hier besprechen wir die Definition: Wie überprüft man die Smith-Nummer in Java? Beispiel mit Code-Implementierung.
 Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
In diesem Artikel haben wir die am häufigsten gestellten Fragen zu Java Spring-Interviews mit ihren detaillierten Antworten zusammengestellt. Damit Sie das Interview knacken können.
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Java 8 führt die Stream -API ein und bietet eine leistungsstarke und ausdrucksstarke Möglichkeit, Datensammlungen zu verarbeiten. Eine häufige Frage bei der Verwendung von Stream lautet jedoch: Wie kann man von einem Foreach -Betrieb brechen oder zurückkehren? Herkömmliche Schleifen ermöglichen eine frühzeitige Unterbrechung oder Rückkehr, aber die Stream's foreach -Methode unterstützt diese Methode nicht direkt. In diesem Artikel werden die Gründe erläutert und alternative Methoden zur Implementierung vorzeitiger Beendigung in Strahlverarbeitungssystemen erforscht. Weitere Lektüre: Java Stream API -Verbesserungen Stream foreach verstehen Die Foreach -Methode ist ein Terminalbetrieb, der einen Vorgang für jedes Element im Stream ausführt. Seine Designabsicht ist
 Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Anleitung zum TimeStamp to Date in Java. Hier diskutieren wir auch die Einführung und wie man Zeitstempel in Java in ein Datum konvertiert, zusammen mit Beispielen.
 Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Kapseln sind dreidimensionale geometrische Figuren, die aus einem Zylinder und einer Hemisphäre an beiden Enden bestehen. Das Volumen der Kapsel kann berechnet werden, indem das Volumen des Zylinders und das Volumen der Hemisphäre an beiden Enden hinzugefügt werden. In diesem Tutorial wird erörtert, wie das Volumen einer bestimmten Kapsel in Java mit verschiedenen Methoden berechnet wird. Kapselvolumenformel Die Formel für das Kapselvolumen lautet wie folgt: Kapselvolumen = zylindrisches Volumenvolumen Zwei Hemisphäre Volumen In, R: Der Radius der Hemisphäre. H: Die Höhe des Zylinders (ohne die Hemisphäre). Beispiel 1 eingeben Radius = 5 Einheiten Höhe = 10 Einheiten Ausgabe Volumen = 1570,8 Kubikeinheiten erklären Berechnen Sie das Volumen mithilfe der Formel: Volumen = π × R2 × H (4
 PHP vs. Python: Verständnis der Unterschiede
Apr 11, 2025 am 12:15 AM
PHP vs. Python: Verständnis der Unterschiede
Apr 11, 2025 am 12:15 AM
PHP und Python haben jeweils ihre eigenen Vorteile, und die Wahl sollte auf Projektanforderungen beruhen. 1.PHP eignet sich für die Webentwicklung mit einfacher Syntax und hoher Ausführungseffizienz. 2. Python eignet sich für Datenwissenschaft und maschinelles Lernen mit präziser Syntax und reichhaltigen Bibliotheken.
 PHP: Eine Schlüsselsprache für die Webentwicklung
Apr 13, 2025 am 12:08 AM
PHP: Eine Schlüsselsprache für die Webentwicklung
Apr 13, 2025 am 12:08 AM
PHP ist eine Skriptsprache, die auf der Serverseite weit verbreitet ist und insbesondere für die Webentwicklung geeignet ist. 1.PHP kann HTML einbetten, HTTP -Anforderungen und Antworten verarbeiten und eine Vielzahl von Datenbanken unterstützt. 2.PHP wird verwendet, um dynamische Webinhalte, Prozessformdaten, Zugriffsdatenbanken usw. mit starker Community -Unterstützung und Open -Source -Ressourcen zu generieren. 3. PHP ist eine interpretierte Sprache, und der Ausführungsprozess umfasst lexikalische Analyse, grammatikalische Analyse, Zusammenstellung und Ausführung. 4.PHP kann mit MySQL für erweiterte Anwendungen wie Benutzerregistrierungssysteme kombiniert werden. 5. Beim Debuggen von PHP können Sie Funktionen wie error_reporting () und var_dump () verwenden. 6. Optimieren Sie den PHP-Code, um Caching-Mechanismen zu verwenden, Datenbankabfragen zu optimieren und integrierte Funktionen zu verwenden. 7
 Gestalten Sie die Zukunft: Java-Programmierung für absolute Anfänger
Oct 13, 2024 pm 01:32 PM
Gestalten Sie die Zukunft: Java-Programmierung für absolute Anfänger
Oct 13, 2024 pm 01:32 PM
Java ist eine beliebte Programmiersprache, die sowohl von Anfängern als auch von erfahrenen Entwicklern erlernt werden kann. Dieses Tutorial beginnt mit grundlegenden Konzepten und geht dann weiter zu fortgeschrittenen Themen. Nach der Installation des Java Development Kit können Sie das Programmieren üben, indem Sie ein einfaches „Hello, World!“-Programm erstellen. Nachdem Sie den Code verstanden haben, verwenden Sie die Eingabeaufforderung, um das Programm zu kompilieren und auszuführen. Auf der Konsole wird „Hello, World!“ ausgegeben. Mit dem Erlernen von Java beginnt Ihre Programmierreise, und wenn Sie Ihre Kenntnisse vertiefen, können Sie komplexere Anwendungen erstellen.






