XOR-Abfrage für den maximalen ungeraden Teiler im Bereich in C++

Gegeben sei ein Array mit N Ganzzahlen und Q-Bereichsabfragen. Für jede Abfrage müssen wir das XOR des größten ungeraden Teilers jeder Zahl im Bereich zurückgeben.
Der größte ungerade Teiler ist die größte ungerade Zahl, die die Zahl N teilen kann, wie zum Beispiel . Beispielsweise ist der größte ungerade Teiler von 6 3.
Input: nums[ ] = { 3, 6, 7, 10 }, query[ ] = { { 0, 2 }, { 1, 3 } }
Output:
query1: 7
query2: 1
Explanation: greatest odd divisors of nums array are { 3, 3, 7, 5 }.
For query 1 we need to find the XOR of indexes 0, 1, and 2 which is 7, and for query2 we need to find XOR of indexes 1, 2, and 3 which is 1.So lösen Sie
Einfache Methode
Zuerst müssen wir bei der einfachen Methode den größten ungeraden Teiler aller Array-Elemente finden. Dann müssen wir basierend auf dem Bereich der Abfrage das XOR jedes Elements im Bereich berechnen und zurückgeben.
Effizienter Ansatz
Eine effiziente Möglichkeit, dieses Problem zu lösen, besteht darin, ein Präfix-XOR-Array prefix_XOR[] zu erstellen, das das Array mit dem größten ungeraden Teiler enthält, anstatt jede Zahl im Bereich jedes Mal per XOR zu verknüpfen und prefix_XOR[R ] - prefix_XOR zurückzugeben [L-1].
Präfix-XOR-Array ist ein Array, bei dem jedes Element das XOR aller vorherigen Elemente enthält.
Beispiel
#include <bits/stdc++.h>
using namespace std;
int main(){
int nums[] = { 3, 6, 7, 10 };
int n = sizeof(nums) / sizeof(nums[0]);
int prefix_XOR[n];
// creating an array
// containing Greatest odd divisor of each element.
for (int i = 0; i < n; i++) {
while (nums[i] % 2 != 1)
nums[i] /= 2;
prefix_XOR[i] = nums[i];
}
// changing prefix_XOR array to prefix xor array.
for (int i = 1; i < n; i++)
prefix_XOR[i] = prefix_XOR[i - 1] ^ prefix_XOR[i];
// query array to find result of these queries.
int query[2][2] = {{0, 2},{1, 3}};
int q = sizeof(query) / sizeof(query[0]);
// finding results of queries.
for(int i = 0;i<q;i++){
if (query[i][0] == 0)
cout<< prefix_XOR[query[i][1]] << endl;
else{
int result = prefix_XOR[query[0][1]] ^ prefix_XOR[query[i][0] - 1];
cout << result << endl;
}
}
return 0;
}Ausgabe
7 4
Obenige Codebeschreibung
Erstellen Sie ein prefix_XOR-Array, um den größten ungeraden Teiler jedes Elements zu speichern, und ändern Sie dieses Array dann in ein Präfix-XOR-Array.
Der größte ungerade Teiler wird berechnet, indem man ihn durch zwei dividiert, bis Modulo 2 1 ergibt.
Erstellen Sie ein Präfix-XOR-Array, indem Sie das Array durchlaufen und eine bitweise XOR-Verknüpfung des aktuellen Elements mit dem vorherigen Element durchführen.
Das Abfrageergebnis wird berechnet, indem der rechte Index des prefix_XOR[]-Arrays (links - 1) vom Index des prefix_XOR[]-Arrays subtrahiert wird.
Fazit
In diesem Tutorial haben wir ein Problem besprochen, bei dem wir den größten ungeraden Teiler für jede Zahl im Bereich eines bestimmten Arrays XOR finden müssen. Wir haben eine Möglichkeit diskutiert, dieses Problem zu lösen, indem wir den größten ungeraden Teiler für jedes Element finden und ein Präfix-XOR-Array verwenden. Wir haben auch ein C++-Programm für dieses Problem besprochen und können dies mit Programmiersprachen wie C, Java, Python usw. tun. Wir hoffen, dass dieser Artikel für Sie hilfreich war.
Das obige ist der detaillierte Inhalt vonXOR-Abfrage für den maximalen ungeraden Teiler im Bereich in C++. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1382
1382
 52
52
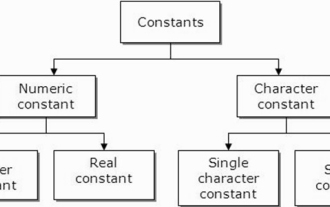 Was sind Konstanten in der C-Sprache? Können Sie ein Beispiel nennen?
Aug 28, 2023 pm 10:45 PM
Was sind Konstanten in der C-Sprache? Können Sie ein Beispiel nennen?
Aug 28, 2023 pm 10:45 PM
Eine Konstante wird auch als Variable bezeichnet. Sobald sie definiert ist, ändert sich ihr Wert während der Ausführung des Programms nicht. Daher können wir eine Variable als Konstante deklarieren, die auf einen festen Wert verweist. Es wird auch Text genannt. Konstanten müssen mit dem Schlüsselwort Const definiert werden. Syntax Die Syntax der in der Programmiersprache C verwendeten Konstanten ist wie folgt: consttypeVariableName; (oder) Verschiedene Arten von Konstanten Die verschiedenen Arten von Konstanten, die in der Programmiersprache C verwendet werden, sind wie folgt: Ganzzahlige Konstanten – Beispiel: 1,0 ,34, 4567 Gleitkommakonstanten – Beispiel: 0,0, 156,89, 23,456 Oktal- und Hexadezimalkonstanten – Beispiel: Hex: 0x2a, 0xaa.. Oktal
 VSCode und VS C++ IntelliSense funktionieren nicht oder rufen keine Bibliotheken auf
Feb 29, 2024 pm 01:28 PM
VSCode und VS C++ IntelliSense funktionieren nicht oder rufen keine Bibliotheken auf
Feb 29, 2024 pm 01:28 PM
VS Code und Visual Studio C++ IntelliSense können Bibliotheken möglicherweise nicht abrufen, insbesondere bei der Arbeit an großen Projekten. Wenn wir mit der Maus über #Include<wx/wx.h> fahren, wird die Fehlermeldung „Quelldatei 'string.h' kann nicht geöffnet werden“ angezeigt (abhängig von „wx/wx.h“) und manchmal reagiert die Funktion zur automatischen Vervollständigung nicht. In diesem Artikel erfahren Sie, was Sie tun können, wenn VSCode und VSC++ IntelliSense nicht funktionieren oder Bibliotheken nicht extrahieren. Warum funktioniert mein Intellisense nicht in C++? Bei der Arbeit mit großen Dateien kommt es manchmal zu IntelliSense
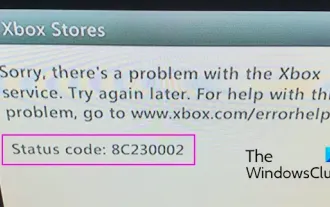 Beheben Sie den Xbox-Fehlercode 8C230002
Feb 27, 2024 pm 03:55 PM
Beheben Sie den Xbox-Fehlercode 8C230002
Feb 27, 2024 pm 03:55 PM
Können Sie aufgrund des Fehlercodes 8C230002 keine Inhalte auf Ihrer Xbox kaufen oder ansehen? Einige Benutzer erhalten diese Fehlermeldung immer wieder, wenn sie versuchen, Inhalte auf ihrer Konsole zu kaufen oder anzusehen. Leider liegt ein Problem mit dem Xbox-Dienst vor. Versuchen Sie es später erneut. Wenn Sie Hilfe zu diesem Problem benötigen, besuchen Sie www.xbox.com/errorhelp. Statuscode: 8C230002 Dieser Fehlercode wird normalerweise durch vorübergehende Server- oder Netzwerkprobleme verursacht. Es kann jedoch auch andere Gründe geben, beispielsweise die Datenschutzeinstellungen oder die Kindersicherung Ihres Kontos, die Sie möglicherweise daran hindern, bestimmte Inhalte zu kaufen oder anzusehen. Beheben Sie den Xbox-Fehlercode 8C230002, wenn Sie beim Versuch, Inhalte auf Ihrer Xbox-Konsole anzusehen oder zu kaufen, den Fehlercode 8C erhalten
 Rekursives Programm zum Ermitteln minimaler und maximaler Elemente eines Arrays in C++
Aug 31, 2023 pm 07:37 PM
Rekursives Programm zum Ermitteln minimaler und maximaler Elemente eines Arrays in C++
Aug 31, 2023 pm 07:37 PM
Als Eingabe nehmen wir das Integer-Array Arr[]. Ziel ist es, mithilfe einer rekursiven Methode die größten und kleinsten Elemente in einem Array zu finden. Da wir Rekursion verwenden, durchlaufen wir das gesamte Array, bis wir Länge = 1 erreichen, und geben dann A[0] zurück, was den Basisfall bildet. Andernfalls wird das aktuelle Element mit dem aktuellen Minimal- oder Maximalwert verglichen und sein Wert für nachfolgende Elemente rekursiv aktualisiert. Schauen wir uns verschiedene Eingabe- und Ausgabeszenarien dafür an −Input −Arr={12,67,99,76,32};Output −Maximum value in the array: 99 Explanation &mi
 China Eastern Airlines gibt bekannt, dass das Passagierflugzeug C919 bald in Betrieb genommen wird
May 28, 2023 pm 11:43 PM
China Eastern Airlines gibt bekannt, dass das Passagierflugzeug C919 bald in Betrieb genommen wird
May 28, 2023 pm 11:43 PM
Laut Nachrichten vom 25. Mai gab China Eastern Airlines bei der Leistungsbesprechung die neuesten Fortschritte beim Passagierflugzeug C919 bekannt. Nach Angaben des Unternehmens ist der mit COMAC unterzeichnete C919-Kaufvertrag im März 2021 offiziell in Kraft getreten und das erste C919-Flugzeug wurde bis Ende 2022 ausgeliefert. Es wird erwartet, dass das Flugzeug bald offiziell in Betrieb genommen wird. China Eastern Airlines wird Shanghai als Hauptbasis für den kommerziellen Betrieb der C919 nutzen und plant die Einführung von insgesamt fünf C919-Passagierflugzeugen in den Jahren 2022 und 2023. Das Unternehmen gab an, dass zukünftige Einführungspläne auf der Grundlage der tatsächlichen Betriebsbedingungen und der Streckennetzplanung festgelegt werden. Nach Auffassung des Herausgebers handelt es sich bei der C919 um Chinas neue Generation globaler Single-Aisle-Hauptlinienpassagierflugzeuge mit völlig unabhängigen geistigen Eigentumsrechten und entspricht international anerkannten Lufttüchtigkeitsstandards. Sollen
 C++-Programm zum Drucken spiralförmiger Zahlenmuster
Sep 05, 2023 pm 06:25 PM
C++-Programm zum Drucken spiralförmiger Zahlenmuster
Sep 05, 2023 pm 06:25 PM
Die Anzeige von Zahlen in verschiedenen Formaten ist eines der grundlegenden Codierungsprobleme beim Lernen. Verschiedene Codierungskonzepte wie bedingte Anweisungen und Schleifenanweisungen. Es gibt verschiedene Programme, in denen wir Sonderzeichen wie Sternchen verwenden, um Dreiecke oder Quadrate zu drucken. In diesem Artikel drucken wir Zahlen in Spiralform, genau wie Quadrate in C++. Wir nehmen die Anzahl der Zeilen n als Eingabe, beginnen in der oberen linken Ecke und bewegen uns nach rechts, dann nach unten, dann nach links, dann nach oben, dann wieder nach rechts und so weiter und so fort. Spiralmuster mit Zahlen 123456724252627282982340414243309223948494431102138474645321120373635343312191817161514
 Die Funktion des Schlüsselworts void in der C-Sprache
Feb 19, 2024 pm 11:33 PM
Die Funktion des Schlüsselworts void in der C-Sprache
Feb 19, 2024 pm 11:33 PM
void ist in C ein spezielles Schlüsselwort, das zur Darstellung eines leeren Typs verwendet wird, also Daten ohne einen bestimmten Typ. In der C-Sprache wird void normalerweise in den folgenden drei Aspekten verwendet. Der Rückgabetyp der Funktion ist void. In der Sprache C können Funktionen unterschiedliche Rückgabetypen haben, z. B. int, float, char usw. Wenn die Funktion jedoch keinen Wert zurückgibt, kann der Rückgabetyp auf void gesetzt werden. Dies bedeutet, dass die Funktion nach Ausführung keinen bestimmten Wert zurückgibt. Zum Beispiel: voidhelloWorld()
 Zum ersten Mal seit 23 Jahren gewinnt C# den TIOBE 2023 Programming Language of the Year Award
Jan 11, 2024 pm 04:45 PM
Zum ersten Mal seit 23 Jahren gewinnt C# den TIOBE 2023 Programming Language of the Year Award
Jan 11, 2024 pm 04:45 PM
Laut dem TIOBE Programming Community Index, einem der Benchmarks zur Messung der Beliebtheit von Programmiersprachen, wird er durch das Sammeln von Daten von Ingenieuren, Kursen, Anbietern und Suchmaschinen auf der ganzen Welt bewertet. Der TIOBE-Index im Januar 2024 wurde kürzlich veröffentlicht und die offizielle Rangliste der Programmiersprachen für 2023 wurde bekannt gegeben. C# wurde zum ersten Mal seit 23 Jahren als TIOBE-Programmiersprache des Jahres ausgezeichnet. In der offiziellen Pressemitteilung von TIOBE heißt es, dass C# seit mehr als 20 Jahren zu den Top 10 gehört und nun zu den vier großen Sprachen aufschließt und sich zur Programmiersprache mit dem größten Wachstum seit einem Jahr entwickelt hat (+1,43 %). Es hat sich diesen Preis mehr als verdient. Auf dem zweiten Platz liegen Scratch (+0,83 %) und Fortran (+0).




