Regressionsanalyse und Best-Fit-Gerade mit Python
In diesem Tutorial implementieren wir eine Regressionsanalyse und eine Best-Fit-Linie mithilfe der Python-Programmierung
Einführung
Die Regressionsanalyse ist die grundlegendste Form der prädiktiven Analyse.
In der Statistik ist die lineare Regression eine Methode zur Modellierung der Beziehung zwischen einem Skalarwert und einer oder mehreren erklärenden Variablen.
Beim maschinellen Lernen ist die lineare Regression ein überwachter Algorithmus. Dieser Algorithmus sagt einen Zielwert basierend auf unabhängigen Variablen voraus.
Weitere Informationen zur linearen Regression und Regressionsanalyse
Bei der linearen Regression/Analyse ist das Ziel ein realer oder kontinuierlicher Wert wie Gehalt, BMI usw. Es wird häufig verwendet, um die Beziehung zwischen einer abhängigen Variablen und einer Reihe unabhängiger Variablen vorherzusagen. Diese Modelle passen typischerweise zu linearen Gleichungen, es gibt jedoch auch andere Arten der Regression, einschließlich Polynome höherer Ordnung.
Bevor ein lineares Modell an die Daten angepasst wird, muss überprüft werden, ob zwischen den Datenpunkten ein linearer Zusammenhang besteht. Dies geht aus ihrem Streudiagramm hervor. Das Ziel des Algorithmus/Modells besteht darin, die Linie mit der besten Anpassung zu finden.
In diesem Artikel werden wir die lineare Regressionsanalyse und ihre Implementierung mit C++ untersuchen.
Die lineare Regressionsgleichung hat die Form Y = c + mx, wobei Y die Zielvariable und X die unabhängige Variable oder erklärende Parameter/Variable ist. m ist die Steigung der Regressionsgeraden und c ist der Achsenabschnitt. Da es sich um eine 2D-Regressionsaufgabe handelt, versucht das Modell während des Trainings, die Linie mit der besten Anpassung zu finden. Es müssen nicht alle Punkte exakt auf derselben Linie liegen. Einige Datenpunkte liegen möglicherweise auf der Linie, andere sind möglicherweise über die Linie verstreut. Der vertikale Abstand zwischen der Linie und den Datenpunkten ist das Residuum. Der Wert kann negativ oder positiv sein, je nachdem, ob der Punkt unterhalb oder oberhalb der Linie liegt. Das Residuum ist ein Maß dafür, wie gut die Linie zu den Daten passt. Der Algorithmus ist kontinuierlich, um das Gesamtresiduum zu minimieren.
Das Residuum für jede Beobachtung ist die Differenz zwischen dem vorhergesagten Wert von y (der abhängigen Variablen) und dem beobachteten Wert von y
$$mathrm{residual: =: tatsächlich: y: Wert:−:Vorhersage: y: Wert}$$
$$mathrm{ri:=:yi:−:y'i}$$
Die gebräuchlichste Metrik zur Bewertung der Leistung eines linearen Regressionsmodells wird als Root Mean Square Error oder RMSE bezeichnet. Die Grundidee besteht darin, zu messen, wie schlecht/falsch die Vorhersagen des Modells im Vergleich zu tatsächlichen Beobachtungen sind.
Ein hoher RMSE ist also „schlecht“ und ein niedriger RMSE ist „gut“
RMSE-Fehler ist
$$mathrm{RMSE:=:sqrt{frac{sum_i^n=1:(this:-:this')^2}{n}}}$$ p>
RMSE ist die Wurzel des mittleren Quadrats aller Residuen.
Implementiert mit Python
Beispiel
# Import the libraries
import numpy as np
import math
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Generate random data with numpy, and plot it with matplotlib:
ranstate = np.random.RandomState(1)
x = 10 * ranstate.rand(100)
y = 2 * x - 5 + ranstate.randn(100)
plt.scatter(x, y);
plt.show()
# Creating a linear regression model based on the positioning of the data and Intercepting, and predicting a Best Fit:
lr_model = LinearRegression(fit_intercept=True)
lr_model.fit(x[:70, np.newaxis], y[:70])
y_fit = lr_model.predict(x[70:, np.newaxis])
mse = mean_squared_error(y[70:], y_fit)
rmse = math.sqrt(mse)
print("Mean Square Error : ",mse)
print("Root Mean Square Error : ",rmse)
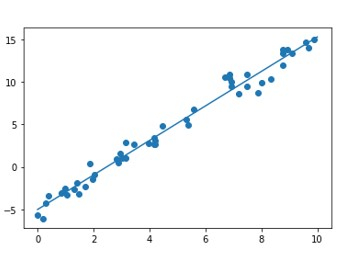
# Plot the estimated linear regression line using matplotlib:
plt.scatter(x, y)
plt.plot(x[70:], y_fit);
plt.show()
Ausgabe
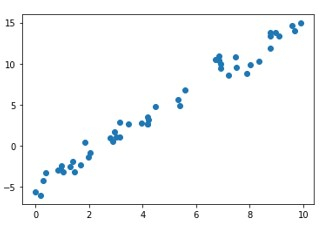
Mean Square Error : 1.0859922470998231 Root Mean Square Error : 1.0421095178050257
Fazit
Die Regressionsanalyse ist eine sehr einfache, aber leistungsstarke Technik, die für prädiktive Analysen beim maschinellen Lernen und in der Statistik verwendet wird. Die Idee liegt in ihrer Einfachheit und der zugrunde liegenden linearen Beziehung zwischen den unabhängigen Variablen und den Zielvariablen.
Das obige ist der detaillierte Inhalt vonRegressionsanalyse und Best-Fit-Gerade mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Restanalysetechniken in Python
Jun 10, 2023 am 08:52 AM
Restanalysetechniken in Python
Jun 10, 2023 am 08:52 AM
Python ist eine weit verbreitete Programmiersprache und seine leistungsstarken Datenanalyse- und Visualisierungsfunktionen machen es zu einem der bevorzugten Werkzeuge für Datenwissenschaftler und Ingenieure für maschinelles Lernen. In diesen Anwendungen ist die Residuenanalyse eine gängige Technik zur Bewertung der Modellgenauigkeit und zur Identifizierung etwaiger Modellverzerrungen. In diesem Artikel stellen wir verschiedene Möglichkeiten zur Verwendung von Restanalysetechniken in Python vor. Residuen verstehen Bevor wir Techniken zur Residuenanalyse in Python einführen, wollen wir zunächst verstehen, was Residuen sind. In der Statistik ist das Residuum die Differenz zwischen dem tatsächlich beobachteten Wert und
 AssertionError: Wie behebe ich Python-Assertionsfehler?
Jun 25, 2023 pm 11:07 PM
AssertionError: Wie behebe ich Python-Assertionsfehler?
Jun 25, 2023 pm 11:07 PM
Behauptungen in Python sind ein nützliches Werkzeug für Programmierer zum Debuggen ihres Codes. Es wird verwendet, um zu überprüfen, ob der interne Status des Programms den Erwartungen entspricht, und um einen Assertionsfehler (AssertionError) auszulösen, wenn diese Bedingungen falsch sind. Während des Entwicklungsprozesses werden beim Testen und Debuggen Assertionen verwendet, um zu überprüfen, ob der Status des Codes mit den erwarteten Ergebnissen übereinstimmt. In diesem Artikel werden die Ursachen, Lösungen und die korrekte Verwendung von Zusicherungen in Ihrem Code erläutert. Ursache des Assertion-Fehlers. Assertion-Fehler bestanden
 Stratifizierte Stichprobentechniken in Python
Jun 10, 2023 pm 10:40 PM
Stratifizierte Stichprobentechniken in Python
Jun 10, 2023 pm 10:40 PM
Die geschichtete Stichprobentechnik in Python ist eine häufig verwendete Datenerfassungsmethode in der Statistik. Sie kann einen Teil der Stichproben aus dem Datensatz zur Analyse auswählen, um auf die Eigenschaften des gesamten Datensatzes zu schließen. Im Zeitalter von Big Data sind die Datenmengen riesig und die Verwendung der gesamten Stichprobe für die Analyse ist sowohl zeitaufwändig als auch wirtschaftlich unpraktisch. Daher kann die Wahl einer geeigneten Stichprobenmethode die Effizienz der Datenanalyse verbessern. In diesem Artikel werden hauptsächlich geschichtete Stichprobentechniken in Python vorgestellt. Was ist eine geschichtete Stichprobe? Bei der Probenahme handelt es sich um eine geschichtete Probenahme
 So entwickeln Sie einen Schwachstellenscanner in Python
Jul 01, 2023 am 08:10 AM
So entwickeln Sie einen Schwachstellenscanner in Python
Jul 01, 2023 am 08:10 AM
Überblick über die Entwicklung eines Schwachstellenscanners mit Python In der heutigen Umgebung zunehmender Sicherheitsbedrohungen im Internet sind Schwachstellenscanner zu einem wichtigen Werkzeug zum Schutz der Netzwerksicherheit geworden. Python ist eine beliebte Programmiersprache, die prägnant, leicht lesbar und leistungsstark ist und sich für die Entwicklung verschiedener praktischer Tools eignet. In diesem Artikel erfahren Sie, wie Sie mit Python einen Schwachstellenscanner entwickeln, der Ihr Netzwerk in Echtzeit schützt. Schritt 1: Scanziele festlegen Bevor Sie einen Schwachstellenscanner entwickeln, müssen Sie festlegen, welche Ziele Sie scannen möchten. Dies kann Ihr eigenes Netzwerk sein oder alles, was Sie testen dürfen
 So verwenden Sie Python für die Skripterstellung und Ausführung unter Linux
Oct 05, 2023 am 11:45 AM
So verwenden Sie Python für die Skripterstellung und Ausführung unter Linux
Oct 05, 2023 am 11:45 AM
So verwenden Sie Python zum Schreiben und Ausführen von Skripten unter Linux. Im Linux-Betriebssystem können wir Python zum Schreiben und Ausführen verschiedener Skripte verwenden. Python ist eine prägnante und leistungsstarke Programmiersprache, die eine Fülle von Bibliotheken und Tools bereitstellt, um die Skripterstellung einfacher und effizienter zu machen. Im Folgenden stellen wir die grundlegenden Schritte zur Verwendung von Python zum Schreiben und Ausführen von Skripten unter Linux vor und stellen einige spezifische Codebeispiele bereit, die Ihnen helfen, es besser zu verstehen und zu verwenden. Installieren Sie Python
 Verwendung der Funktion sqrt() in Python
Feb 21, 2024 pm 03:09 PM
Verwendung der Funktion sqrt() in Python
Feb 21, 2024 pm 03:09 PM
Verwendung und Codebeispiele der Funktion sqrt() in Python 1. Funktion und Einführung der Funktion sqrt() In der Python-Programmierung ist die Funktion sqrt() eine Funktion im Mathematikmodul und ihre Funktion besteht darin, die Quadratwurzel von zu berechnen eine Zahl. Die Quadratwurzel bedeutet, dass eine mit sich selbst multiplizierte Zahl dem Quadrat der Zahl entspricht, d. h. x*x=n, dann ist x die Quadratwurzel von n. Zur Berechnung der Quadratwurzel kann im Programm die Funktion sqrt() verwendet werden. 2. So verwenden Sie die Funktion sqrt() in Python, sq
 Python-Programmierpraxis: Verwendung der Baidu Map API zum Generieren statischer Kartenfunktionen
Jul 30, 2023 pm 09:05 PM
Python-Programmierpraxis: Verwendung der Baidu Map API zum Generieren statischer Kartenfunktionen
Jul 30, 2023 pm 09:05 PM
Python-Programmierpraxis: Verwendung der Baidu Map API zum Generieren statischer Kartenfunktionen Einführung: In der modernen Gesellschaft sind Karten zu einem unverzichtbaren Bestandteil des Lebens der Menschen geworden. Bei der Arbeit mit Karten benötigen wir häufig eine statische Karte eines bestimmten Bereichs zur Anzeige auf einer Webseite, einer mobilen App oder einem Bericht. In diesem Artikel wird die Verwendung der Programmiersprache Python und der Baidu Map API zum Generieren statischer Karten vorgestellt und relevante Codebeispiele bereitgestellt. 1. Vorbereitungsarbeiten Um die Funktion der Generierung statischer Karten mithilfe der Baidu Map API zu realisieren, I
 Python-Programmierung zur Analyse der Koordinatenkonvertierungsfunktion in der Baidu Map API-Dokumentation
Aug 01, 2023 am 08:57 AM
Python-Programmierung zur Analyse der Koordinatenkonvertierungsfunktion in der Baidu Map API-Dokumentation
Aug 01, 2023 am 08:57 AM
Python-Programmierung zur Analyse der Koordinatenkonvertierungsfunktion in der Baidu Map API-Dokumentation Einführung: Mit der rasanten Entwicklung des Internets ist die Kartenpositionierungsfunktion zu einem unverzichtbaren Bestandteil des Lebens moderner Menschen geworden. Als einer der beliebtesten Kartendienste in China stellt Baidu Maps eine Reihe von APIs für Entwickler zur Verfügung. In diesem Artikel wird die Python-Programmierung verwendet, um die Koordinatenkonvertierungsfunktion in der Baidu Map API-Dokumentation zu analysieren und entsprechende Codebeispiele zu geben. 1. Einleitung Bei der Entwicklung kommt es manchmal zu Problemen bei der Koordinatenkonvertierung. Baidu-Karte AP




