C-Programm zur Überprüfung, ob die Matrix antisymmetrisch ist?

Wenn die Elemente der quadratischen Matrix A aij=−aji für alle i und j erfüllen, dann wird die quadratische Matrix A als antisymmetrische Matrix bezeichnet. Mit anderen Worten, wenn die Transponierte von Matrix A gleich dem negativen Wert von Matrix A ist, also (AT=−A), dann wird Matrix A als antisymmetrische Matrix bezeichnet.
Beachten Sie, dass alle Hauptdiagonalelemente einer antisymmetrischen Matrix Null sind.
Nehmen wir ein Beispiel einer Matrix
A= |0 -5 4| |5 0 -1| |-4 1 0|
Dies ist eine schiefsymmetrische Matrix, da für alle i und j aij=−aji gilt. Zum Beispiel a12 = -5, a21 = 5, was a12 = −a21 bedeutet. Ebenso gilt diese Bedingung für alle anderen Werte von i und j.
Wir können auch überprüfen, ob die Transponierte von Matrix A gleich dem Negativ von Matrix A ist, d. h. AT=−A.
A<sup>T</sup>= |0 5 -4|
|-5 0 1|
|4 -1 0|
and
A= |0 -5 4|
|5 0 -1|
|-4 1 0|Wir können deutlich erkennen, dass AT=−A ist, was A zu einer schiefsymmetrischen Matrix macht.
Input: Enter the number of rows and columns: 2 2 Enter the matrix elements: 10 20 20 10 Output: The matrix is symmetric. 10 20 20 10
Erklärung
Eine Matrix ist eine symmetrische Matrix, wenn sie gleich ihrer Transponierten ist.
Andernfalls ist die Matrix antisymmetrisch, wenn ihre Transponierte gleich ihrem Negativ ist. Ansonsten ist es weder symmetrisch noch antisymmetrisch. Die Ergebnisse werden entsprechend ausgedruckt.
Der Prozess zum Überprüfen der Symmetrie einer Matrix ist wie folgt:
Der Benutzer muss die Anzahl der Zeilen und Spalten der Matrix eingeben.
Benötigt die Elemente der Eingabematrix und speichert sie in „A“. Initialisieren Sie die Variablen „x“ und „y“ auf 0.
Wenn die Matrix nicht gleich ihrer Transponierten ist, weisen Sie der temporären Variablen „x“ den Wert 1 zu.
Andernfalls, wenn das Negativ der Matrix gleich ihrer Transponierten ist, weisen Sie der temporären Variablen „y“ den Wert 1 zu.
Wenn x gleich 0 ist, dann ist die Matrix symmetrisch. Andernfalls ist die Matrix antisymmetrisch, wenn y gleich 1 ist.
Wenn keine der oben genannten Bedingungen erfüllt ist, ist die Matrix weder symmetrisch noch antisymmetrisch.
Dann drucken Sie das Ergebnis aus.
Beispiel
#include<iostream>
using namespace std;
int main () {
int A[10][10], i, j, m, n, x = 0, y = 0;
cout << "Enter the number of rows and columns : ";
cin >> m >> n;
cout << "Enter the matrix elements : ";
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
cin >> A[i][j];
for (i = 0; i < m; i++) {
for( j = 0; j < n; j++) {
if (A[i][j] != A[j][i])
x = 1;
else if (A[i][j] == -A[j][i])
y = 1;
}
}
if (x == 0)
cout << "The matrix is symmetric.</p><p> ";
else if (y == 1)
cout << "The matrix is skew symmetric.</p><p> ";
else
cout << "It is neither symmetric nor skew-symmetric.</p><p> ";
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++)
cout << A[i][j] << " ";
cout << "</p><p> ";
}
return 0;
}Das obige ist der detaillierte Inhalt vonC-Programm zur Überprüfung, ob die Matrix antisymmetrisch ist?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Übersetzen Sie Folgendes ins Chinesische: C-Programm zur Konvertierung römischer Ziffern in Dezimalzahlen
Sep 05, 2023 pm 09:53 PM
Übersetzen Sie Folgendes ins Chinesische: C-Programm zur Konvertierung römischer Ziffern in Dezimalzahlen
Sep 05, 2023 pm 09:53 PM
Nachfolgend finden Sie einen C-Sprachalgorithmus zum Konvertieren römischer Ziffern in Dezimalzahlen: Algorithmus Schritt 1 – Start Schritt 2 – Römische Ziffern zur Laufzeit lesen Schritt 3 – Länge: = strlen(roman) Schritt 4 – Für i=0 bis Länge-1 Schritt 4.1-switch(roman[i]) Schritt 4.1.1-case'm': &nbs
 Erkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2)
Nov 20, 2023 pm 05:25 PM
Erkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2)
Nov 20, 2023 pm 05:25 PM
Im ersten Artikel dieser Reihe haben wir die Zusammenhänge und Unterschiede zwischen künstlicher Intelligenz, maschinellem Lernen, Deep Learning, Datenwissenschaft und mehr diskutiert. Wir haben auch einige schwierige Entscheidungen hinsichtlich der Programmiersprachen, Tools und mehr getroffen, die in der gesamten Serie verwendet werden sollen. Abschließend haben wir noch ein wenig Matrixwissen eingeführt. In diesem Artikel werden wir die Matrix, den Kern der künstlichen Intelligenz, ausführlich besprechen. Aber vorher wollen wir zunächst die Geschichte der künstlichen Intelligenz verstehen. Warum müssen wir die Geschichte der künstlichen Intelligenz verstehen? In der Geschichte gab es viele KI-Booms, aber in vielen Fällen blieben die großen Erwartungen an das Potenzial der KI aus. Das Verständnis der Geschichte der künstlichen Intelligenz kann uns helfen zu erkennen, ob diese Welle der künstlichen Intelligenz Wunder bewirken wird oder nur eine weitere Blase ist, die kurz vor dem Platzen steht. uns
 C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
Hyperbelfunktionen werden mithilfe von Hyperbeln anstelle von Kreisen definiert und entsprechen gewöhnlichen trigonometrischen Funktionen. Es gibt den Verhältnisparameter in der hyperbolischen Sinusfunktion aus dem angegebenen Winkel im Bogenmaß zurück. Aber machen Sie das Gegenteil, oder anders gesagt. Wenn wir einen Winkel aus einem hyperbolischen Sinus berechnen wollen, benötigen wir eine umgekehrte hyperbolische trigonometrische Operation wie die hyperbolische Umkehrsinusoperation. In diesem Kurs wird gezeigt, wie Sie die hyperbolische Umkehrsinusfunktion (asinh) in C++ verwenden, um Winkel mithilfe des hyperbolischen Sinuswerts im Bogenmaß zu berechnen. Die hyperbolische Arkussinusoperation folgt der folgenden Formel -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Wo\:In\:ist\:natürlicher Logarithmus\:(log_e\:k)
 C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
Eine Karte ist ein spezieller Containertyp in C++, bei dem jedes Element ein Paar aus zwei Werten ist, nämlich einem Schlüsselwert und einem zugeordneten Wert. Der Schlüsselwert wird zum Indizieren jedes Elements verwendet, und der zugeordnete Wert ist der mit dem Schlüssel verknüpfte Wert. Unabhängig davon, ob der zugeordnete Wert eindeutig ist, ist der Schlüssel immer eindeutig. Um Kartenelemente in C++ zu drucken, müssen wir einen Iterator verwenden. Ein Element in einer Menge von Elementen wird durch ein Iteratorobjekt angegeben. Iteratoren werden hauptsächlich mit Arrays und anderen Arten von Containern (z. B. Vektoren) verwendet und verfügen über einen bestimmten Satz von Operationen, mit denen bestimmte Elemente innerhalb eines bestimmten Bereichs identifiziert werden können. Iteratoren können inkrementiert oder dekrementiert werden, um auf verschiedene Elemente in einem Bereich oder Container zu verweisen. Der Iterator zeigt auf den Speicherort eines bestimmten Elements im Bereich. Drucken einer Karte in C++ mit Iteratoren Schauen wir uns zunächst an, wie man definiert
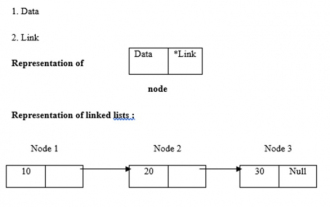 C-Programm zum Ermitteln der Länge einer verknüpften Liste
Sep 07, 2023 pm 07:33 PM
C-Programm zum Ermitteln der Länge einer verknüpften Liste
Sep 07, 2023 pm 07:33 PM
Verknüpfte Listen verwenden eine dynamische Speicherzuweisung, d. h. sie wachsen und schrumpfen entsprechend. Sie werden als Ansammlungen von Knoten definiert. Hier besteht ein Knoten aus zwei Teilen: Daten und Links. Die Darstellung von Daten, Links und verknüpften Listen ist wie folgt: - Arten von verknüpften Listen Es gibt vier Arten von verknüpften Listen: - Einfach verknüpfte Liste / Einfach verknüpfte Liste Doppelt / Doppelt verknüpfte Liste Zirkuläre einfach verknüpfte Liste Zirkuläre doppelt verknüpfte Liste Wir Verwenden Sie die rekursive Methode, um die Länge der verknüpften Liste zu ermitteln. Die Logik lautet -intlength(node *temp){ if(temp==NULL) returnl;
 Python-Programm zum Multiplizieren zweier Matrizen mithilfe mehrdimensionaler Arrays
Sep 11, 2023 pm 05:09 PM
Python-Programm zum Multiplizieren zweier Matrizen mithilfe mehrdimensionaler Arrays
Sep 11, 2023 pm 05:09 PM
Eine Matrix ist eine Menge von Zahlen, die in Zeilen und Spalten angeordnet sind. Eine Matrix mit m Zeilen und n Spalten wird als mXn-Matrix bezeichnet, und m und n werden als ihre Dimensionen bezeichnet. Eine Matrix ist ein zweidimensionales Array, das in Python mithilfe von Listen oder NumPy-Arrays erstellt wird. Im Allgemeinen kann die Matrixmultiplikation durch Multiplikation der Zeilen der ersten Matrix mit den Spalten der zweiten Matrix erfolgen. Dabei sollte die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix sein. Eingabe- und Ausgabeszenario Angenommen, wir haben zwei Matrizen A und B. Die Abmessungen dieser beiden Matrizen betragen 2X3 bzw. 3X2. Die resultierende Matrix nach der Multiplikation hat 2 Zeilen und 1 Spalte. [b1,b2][a1,a2,a3]*[b3,b4]=[a1*b1+a2*b2+a3*a3][a4,a5,a6][b5,b6][a4*b2+a
 C-Programm zur Implementierung des euklidischen Algorithmus
Sep 17, 2023 pm 12:41 PM
C-Programm zur Implementierung des euklidischen Algorithmus
Sep 17, 2023 pm 12:41 PM
Das Problem implementiert den euklidischen Algorithmus, um den größten gemeinsamen Teiler (GCD) und das kleinste gemeinsame Vielfache (LCM) zweier Ganzzahlen zu finden, und gibt die Ergebnisse mit einer gegebenen Ganzzahl aus. Lösung Die Lösung zur Implementierung des euklidischen Algorithmus zum Ermitteln des größten gemeinsamen Teilers (GCD) und des kleinsten gemeinsamen Vielfachen (LCM) zweier Ganzzahlen lautet wie folgt – die Logik zum Ermitteln von GCD und LCM lautet wie folgt – if (firstno*secondno!=0) { gcd= gcd_rec(firstno,secondno); printf("TheGCDof%dand%dis%d",
 Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Die Umbenennungsfunktion ändert den alten Namen einer Datei oder eines Verzeichnisses in den neuen Namen. Dieser Vorgang ähnelt dem Verschiebevorgang. Wir können diese Umbenennungsfunktion also auch zum Verschieben von Dateien verwenden. Diese Funktion ist in der Headerdatei der stdio.h-Bibliothek vorhanden. Die Syntax der Umbenennungsfunktion lautet wie folgt: intrename(constchar*oldname,constchar*newname); Die Funktion der rename()-Funktion akzeptiert zwei Parameter. Einer ist alter Name und der andere ist neuer Name. Beide Parameter sind Zeiger auf konstante Zeichen, die den alten und neuen Namen der Datei definieren. Gibt Null zurück, wenn die Datei erfolgreich umbenannt wurde; andernfalls wird eine Ganzzahl ungleich Null zurückgegeben. Während eines Umbenennungsvorgangs






