Die Summe aller Paare kürzester Pfade im Baum

In Bäumen bezieht sich der Begriff „Summe der kürzesten Pfade über alle Knotenpaare“ auf die Berechnung der Summe der einzelnen kürzesten Pfade für alle Knotenpaare. Eine effektive Methode ist die Verwendung des dualen DFS-Algorithmus (Tiefensuche). Der Abstand zwischen dem ausgewählten Knoten und jedem anderen Knoten wird während des ersten DFS-Durchlaufs bestimmt. Der Baum wird während des zweiten DFS-Durchlaufs erneut durchlaufen, wobei jeder Knoten als potenzieller LCA (niedrigster gemeinsamer Vorfahre) betrachtet und die Summe der Abstände zwischen Paaren von Nachkommenknoten des ausgewählten LCA berechnet wird. Mit dieser Methode können Sie die Summe der kürzesten Pfade für alle Knotenpaare im Baum berechnen und eine ideale Lösung sicherstellen
Anwendungsmethode
Doppelte DFS-Methode (Tiefensuche).
Dynamische Programmiermethode
Doppelte DFS-Methode (Depth First Search)
Für die Summe aller Paare kürzester Pfade im Baum verwenden wir eine duale DFS-Methode (Tiefensuche), die zwei DFS-Durchgänge umfasst. Zuerst berechnen wir den Abstand von jedem Knoten zu allen anderen Knoten. Während des zweiten DFS-Durchlaufs navigieren wir dann durch den Baum und betrachten dabei jeden Knoten als potenziellen LCA. Wir berechnen und summieren die Abstände zwischen Knotenpaaren, die während der Durchquerung Nachkommen des ausgewählten LCA sind. Indem wir diesen Vorgang für alle Knoten wiederholen, erhalten wir die Summe aller Paare kürzester Pfade. Diese Strategie ist für dieses Problem sehr überzeugend, da sie effektiv die Summe der Abstände zwischen allen Knotensätzen im Baum berechnet.
Algorithmus
Jeder Knoten im Baum kann als Startknoten verwendet werden
Um die Entfernung vom ausgewählten Startknoten zu allen anderen Knoten zu bestimmen, führen Sie eine Tiefensuche (DFS) ausgehend von diesem Knoten durch. Diese Abstände sollten in einem Array oder einer Datenstruktur gespeichert werden.
Als nächstes führen Sie eine zweite Tiefensuche (DFS) im Baum durch und betrachten dabei jeden Knoten als seinen möglichen nächsten gemeinsamen Vorfahren (LCA).
Berechnen Sie beim Durchlaufen des Baums während des zweiten DFS den Abstand zwischen Knotenpaaren, die Nachkommen des ausgewählten LCA sind. Für jede LCA werden diese Distanzen addiert.
Wiederholen Sie diesen Vorgang für jeden Knoten im Baum
Die Summe aller Übereinstimmungen auf die endlichste Art im Baum wird durch die Summe aller in Schritt 4 berechneten Abstände dargestellt.
Beispiel
lautet:Beispiel
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
vector<int> graph[MAXN];
int ancestor[MAXN];
int dfs(int node, int lca, int distance) {
int sum = 0;
for (int neighbor : graph[node]) {
if (neighbor != lca) {
sum += dfs(neighbor, lca, distance + 1);
}
}
return sum + distance;
}
int main() {
int lca_node = 0;
int total_sum = 0;
for (int node = 0; node < MAXN; ++node) {
if (node != lca_node) {
total_sum += dfs(node, lca_node, 0);
}
}
cout << "Total sum of distances between descendants of the LCA: " << total_sum << endl;
return 0;
}
Ausgabe
Total sum of distances between descendants of the LCA: 0
Dynamische Programmiermethode:
Wir wählen zunächst einen beliebigen Knoten als Wurzelknoten aus und wandeln den Baum im dynamischen Programmierverfahren in einen Wurzelbaum um, mit dem die Summe der kürzesten Pfade zwischen allen Knoten im Baum berechnet wird. Wir verwenden dynamische Programmierung, um die Aufteilung zwischen jedem Knoten und dem Wurzelknoten zu berechnen und die Ergebnisse in einem Array zu speichern. Dann addieren wir für jeden Knoten die (berechneten) Abstände seiner untergeordneten Knoten vom Wurzelknoten, um den Gesamtabstand aller anderen Knoten zu bestimmen. Auf diese Weise können wir schnell die Gesamtzahl der kürzesten Wege zwischen allen Knoten berechnen. Um dieses Problem effizient zu lösen, beträgt die zeitliche Komplexität dieses Algorithmus O(N), wobei N die Anzahl der Knoten im Baum ist.
Algorithmus
Nehmen Sie einen beliebigen Knoten im Baum als Wurzel und verwurzeln Sie den Baum (z. B. mithilfe einer Tiefensuche des Wurzelknotens), um einen verwurzelten Baum zu erstellen.
Dynamische Programmierung kann verwendet werden, um den Abstand jedes Knotens von der Wurzel zu bestimmen. Diese Abstände sollten in einem Array oder einer Datenstruktur gespeichert werden.
Berechnen Sie die Summe der Abstände von jedem Knoten zu allen anderen Knoten im Baum:
Die Summe aller Paare kürzester Pfade im Baum ist das Endergebnis.
a. Durchlaufen Sie die untergeordneten Knoten des aktuellen Knotens.
b. Um den Pfad durch den aktuellen Knoten zu berücksichtigen, addieren Sie die Anzahl der Knoten im Teilbaum und den zuvor für jeden Teilbaum berechneten Abstand zur Wurzel.
c. Addieren Sie für jeden untergeordneten Knoten des aktiven Knotens diese Beträge
d. Addieren Sie die Gesamtsumme des aktuellen Knotens zum Endergebnis.
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
};
int dfs(TreeNode* node, vector<int>& distances) {
int subtree_size = 1;
for (TreeNode* child : node->children) {
subtree_size += dfs(child, distances);
distances[node->val] += distances[child->val] + subtree_size;
}
return subtree_size;
}
int sumOfAllPairShortestPaths(TreeNode* root) {
vector<int> distances(root->val + 1, 0);
dfs(root, distances);
int total_sum = 0;
for (int distance : distances) {
total_sum += distance;
}
return total_sum;
}
int main() {
TreeNode* root = new TreeNode{0};
int result = sumOfAllPairShortestPaths(root);
cout << "Sum of all pair shortest paths in the tree: " << result << endl;
return 0;
}
Ausgabe
Sum of all pair shortest paths in the tree: 0
Fazit
Die Summe aller Paare kürzester Pfade im Baum kann mithilfe der Double DFS-Methode (Depth First Search) oder dynamischer Programmierung berechnet werden. Die Double-DFS-Methode besteht aus zwei Durchgängen: Zuerst wird der Abstand vom ausgewählten Knoten zu allen anderen Knoten berechnet und dann wird der Baum erneut durchlaufen, wobei jeder Knoten als potenzieller niedrigster gemeinsamer Vorfahre (LCA) behandelt wird, um die Abstände zwischen Descendant-Knotenpaaren zu summieren. Dynamische Programmiermethoden erfordern die rekursive Verwendung von DFS, um die Wurzel des Baums zu erstellen und den Abstand von der Wurzel zu jedem anderen Knoten zu berechnen. Das Ergebnis beider Methoden ist das gleiche und besteht aus der Summe aller paarweise kürzesten Pfade im Baum. Die Entscheidung zwischen zwei Algorithmen kann auf spezifischen Implementierungspräferenzen oder Baumstrukturen basieren, aber beide Algorithmen bieten effiziente Lösungen.
Das obige ist der detaillierte Inhalt vonDie Summe aller Paare kürzester Pfade im Baum. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Die Summe aller Paare kürzester Pfade im Baum
Aug 28, 2023 pm 03:17 PM
Die Summe aller Paare kürzester Pfade im Baum
Aug 28, 2023 pm 03:17 PM
In Bäumen bezieht sich der Begriff „Summe der kürzesten Wege aller Knotenpaare“ auf die Berechnung der Summe der einzelnen kürzesten Wege aller Knotenpaare. Eine effektive Methode ist die Verwendung des dualen DFS-Algorithmus (Tiefensuche). Der Abstand zwischen dem ausgewählten Knoten und jedem anderen Knoten wird während des ersten DFS-Durchlaufs bestimmt. Der Baum wird während des zweiten DFS-Durchlaufs erneut durchlaufen, wobei jeder Knoten als potenzieller LCA (niedrigster gemeinsamer Vorfahre) betrachtet und die Summe der Abstände zwischen Paaren von Nachkommenknoten des ausgewählten LCA berechnet wird. Mit dieser Methode können Sie die Summe der kürzesten Pfade für alle Knotenpaare im Baum berechnen und eine ideale Lösung sicherstellen. Verwendete Methoden Duale DFS-Methode (Depth First Search) Dynamische Programmiermethode Duale DFS-Methode (Depth First Search) für den Baum Alle Paare kürzester Wege
 So implementieren Sie den Kürzeste-Pfad-Algorithmus mit Java
Sep 19, 2023 am 08:18 AM
So implementieren Sie den Kürzeste-Pfad-Algorithmus mit Java
Sep 19, 2023 am 08:18 AM
Überblick über die Verwendung von Java zur Implementierung des Kürzeste-Pfad-Algorithmus: Der Kürzeste-Pfad-Algorithmus ist eine wichtige Anwendung in der Graphentheorie und wird häufig in der Netzwerkrouting-, Kartennavigation- und anderen Bereichen verwendet. In diesem Artikel erfahren Sie, wie Sie den Kürzeste-Pfad-Algorithmus mit Java implementieren und stellen konkrete Codebeispiele bereit. Algorithmusidee: Es gibt viele Möglichkeiten, den Kürzeste-Pfad-Algorithmus zu implementieren. Die beiden bekanntesten Algorithmen sind der Dijkstra-Algorithmus und der A*-Algorithmus. Hier konzentrieren wir uns auf die Implementierung des Dijkstra-Algorithmus. Die Grundlage des Dijkstra-Algorithmus
 Eingehende Untersuchung der Anwendungs- und Implementierungsmethoden nichtlinearer Datenstrukturen von Bäumen und Diagrammen in Java
Dec 26, 2023 am 10:22 AM
Eingehende Untersuchung der Anwendungs- und Implementierungsmethoden nichtlinearer Datenstrukturen von Bäumen und Diagrammen in Java
Dec 26, 2023 am 10:22 AM
Bäume und Diagramme in Java verstehen: Anwendungen und Implementierungen nichtlinearer Datenstrukturen erkunden Einführung In der Informatik sind Datenstrukturen die Art und Weise, wie Daten in Computern gespeichert, organisiert und verwaltet werden. Datenstrukturen können in lineare Datenstrukturen und nichtlineare Datenstrukturen unterteilt werden. Bäume und Diagramme sind die beiden am häufigsten verwendeten Arten nichtlinearer Datenstrukturen. Dieser Artikel konzentriert sich auf die Konzepte, Anwendungen und Implementierung von Bäumen und Diagrammen in Java und gibt spezifische Codebeispiele. Das Konzept und die Anwendung von Baum Ein Baum ist ein abstrakter Datentyp, eine Sammlung von Knoten und Kanten. Jeder Knoten des Baums enthält eine Zahl
 Die wunderbare Verwendung der Rekursion in C++-Datenstrukturen: Implementierung von Stapeln und Bäumen
May 04, 2024 pm 01:54 PM
Die wunderbare Verwendung der Rekursion in C++-Datenstrukturen: Implementierung von Stapeln und Bäumen
May 04, 2024 pm 01:54 PM
Anwendung der Rekursion in C++-Datenstrukturen: Stapel: Der Stapel wird rekursiv durch die Last-In-First-Out-Struktur (LIFO) implementiert. Baum: Baum wird rekursiv durch eine hierarchische Struktur implementiert und unterstützt Vorgänge wie Einfügen und Tiefenberechnung. Rekursion bietet eine prägnante und effiziente Lösung für die Verarbeitung verschachtelter Strukturen und macht die Implementierung von Datenstrukturen intuitiver und einfacher zu warten.
 Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten
Sep 20, 2023 pm 02:21 PM
Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten
Sep 20, 2023 pm 02:21 PM
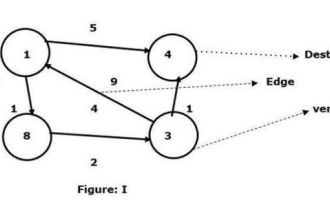
C++ verfügt über ein Makro, das als Codeabschnitt oder erwarteter Wert definiert ist und immer dann wiederverwendet wird, wenn der Benutzer es benötigt. Der Floyd-Walshall-Algorithmus ist der Prozess, den kürzesten Weg zwischen allen Scheitelpunktpaaren in einem gegebenen gewichteten Graphen zu finden. Der Algorithmus folgt einem dynamischen Programmieransatz, um den Minimalgewichtsgraphen zu finden. Lassen Sie uns die Bedeutung des Floyd-Walshall-Algorithmus anhand eines Diagramms verstehen: Nehmen Sie Scheitelpunkt 1 als Quelle und Scheitelpunkt 4 als Ziel und finden Sie den kürzesten Weg zwischen ihnen. Wir haben gesehen, dass es zwei Pfade gibt, die mit dem Zielscheitelpunkt 4 verbunden werden können. 1->4 – die Kante hat ein Gewicht von 51->8->3->4 – das Kantengewicht (1+2+1) ist 4. Im gegebenen Diagramm I sehen wir die kleinste Kante, die zwei Eckpunkte verbindet. Hier also der Scheitelpunkt
 Designideen für PHP-Algorithmen: Wie erreicht man eine effiziente Lösung für das Kürzeste-Wege-Problem von Graphen?
Sep 19, 2023 pm 03:43 PM
Designideen für PHP-Algorithmen: Wie erreicht man eine effiziente Lösung für das Kürzeste-Wege-Problem von Graphen?
Sep 19, 2023 pm 03:43 PM
Designideen für PHP-Algorithmen: Wie erreicht man eine effiziente Lösung für das Kürzeste-Wege-Problem von Graphen? In der tatsächlichen Entwicklung müssen wir häufig das Problem des kürzesten Weges lösen, beispielsweise in der Kartennavigation, Netzwerkrouting, Logistikverteilung und anderen Bereichen. Der Schlüssel zur Lösung dieser Art von Problemen ist der Kürzeste-Weg-Algorithmus für Graphen. Ein Graph besteht aus einer Menge von Eckpunkten und einer Menge von Kanten. Scheitelpunkte stellen Knoten dar und Kanten stellen Beziehungen zwischen Knoten dar. Das Problem des kürzesten Weges besteht darin, den kürzesten Weg zu finden, der zwei Knoten verbindet. In PHP können wir verschiedene Algorithmen verwenden, um das Problem des kürzesten Pfades zu lösen. Der bekannteste davon ist
 Verwenden Sie C++, um alle Knoten zu löschen, die sich auf keinem Pfad befinden und deren Pfadsumme kleiner als k ist
Sep 04, 2023 am 10:17 AM
Verwenden Sie C++, um alle Knoten zu löschen, die sich auf keinem Pfad befinden und deren Pfadsumme kleiner als k ist
Sep 04, 2023 am 10:17 AM
Bei diesem Problem haben wir einen Binärbaum, dessen Pfad vom Wurzelknoten zum Blattknoten vollständig definiert ist. Die Summe aller Knoten vom Wurzelknoten bis zu den Blattknoten muss größer oder gleich k sein. Wir müssen also alle Knoten im Pfad löschen, deren Summe kleiner als k ist. Hier ist es wichtig zu bedenken, dass ein Knoten Teil vieler Pfade sein kann. Daher müssen wir ihn nur dann beschneiden und entfernen, wenn die Summe aller verbleibenden Pfade 10+20+5 beträgt, also 25, also weniger als 150 5 . Danach werten wir 10->30->40 aus. Es ist weniger als 150, also streichen Sie 40. Jetzt sehen wir einen anderen Pfad 10->20->35->50 und die Summe 115 ist kleiner als 150, also
 C++-Programm zum Entfernen von Knoten, die den Pfad nicht erfüllen und größer oder gleich k sind
Sep 14, 2023 am 11:25 AM
C++-Programm zum Entfernen von Knoten, die den Pfad nicht erfüllen und größer oder gleich k sind
Sep 14, 2023 am 11:25 AM
Bei diesem Problem haben wir einen Binärbaum, dessen Pfad vom Wurzelknoten zum Blattknoten vollständig definiert ist. Die Summe aller Knoten vom Wurzelknoten bis zu den Blattknoten muss größer oder gleich dem konstanten Wert k sein. Daher müssen wir alle Knoten in den Pfaden löschen, deren Summe kleiner als k ist, damit die verbleibenden Pfade im Baum größer als k sind. Hier ist es wichtig zu bedenken, dass ein Knoten Teil vieler Pfade sein kann. Daher benötigen wir nur dann, wenn die Summe aller Pfade, die zu diesem Knoten links führen, 10+20+5 ergibt, also 25, also weniger als 150 zum Trimmen und Entfernen 5. Danach werten wir 10->30->40 aus. Der Wert liegt unter 150, daher wird 40 gelöscht. Jetzt sehen wir einen anderen Pfad 10->20-






