Ein Matrixwahrscheinlichkeitsproblem?

Hier sehen wir ein Matrixwahrscheinlichkeitsproblem. Wir haben eine rechteckige Matrix. Wir können uns von der aktuellen Zelle aus mit gleicher Wahrscheinlichkeit in vier Richtungen bewegen. Die vier Richtungen sind links, rechts, oben und unten. Wir wollen die Wahrscheinlichkeit nach N Bewegungen ausgehend von der Position M[i,j] berechnen.
Hier werden wir einige Dinge im Zusammenhang mit DFS tun. Wir werden die vier möglichen Räume ausgehend vom aktuellen Raum rekursiv durchqueren. Dann berechnen wir die Wahrscheinlichkeit, einen Schritt weniger zu machen. Da die vier Richtungen die gleiche Wahrscheinlichkeit haben, trägt jede Richtung 0,25 zur Gesamtwahrscheinlichkeit bei. Wir geben 0 zurück, wenn eine Matrixgrenze überschritten wird, und 1, wenn N Züge abgeschlossen sind. Schauen wir uns den Algorithmus an, um auf diese Idee zu kommen.
Algorithmus
matProb(m, n, x, y, N)
Begin if x,y is not in matrix boundary m, n, then return 0 if N is 0 , then return 1 prob := 0 prob := prob + matProb(m, n, x-1, y, N-1) * 0.25 prob := prob + matProb(m, n, x+1, y, N-1) * 0.25 prob := prob + matProb(m, n, x, y+1, N-1) * 0.25 prob := prob + matProb(m, n, x, y-1, N-1) * 0.25 return prob End
Beispiel
#include<iostream>
using namespace std;
bool isSafe(int x, int y, int m, int n) { //function to check whether (x,y)
is in matrix or not
if(x >= 0 && x < m && y >= 0 && y < n){
return true;
}
return false;
}
double matProb(int m, int n, int x, int y, int N) {
if (!isSafe(x, y, m, n)) //if coundary is crossed
return 0.0;
if (N == 0) //when N is 0, or N is completed, return 1
return 1.0;
double probability = 0.0;
probability += matProb(m, n, x - 1, y, N - 1) * 0.25; //move left
probability += matProb(m, n, x, y + 1, N - 1) * 0.25; //move up
probability += matProb(m, n, x + 1, y, N - 1) * 0.25; //move right
probability += matProb(m, n, x, y - 1, N - 1) * 0.25; //move down
return probability;
}
int main() {
int m = 7, n = 8;
int x = 1, y = 1;
int N = 4;
cout << "Matrix Probability is " << matProb(m, n, x, y, N);
}Ausgabe
Matrix Probability is 0.664062
Das obige ist der detaillierte Inhalt vonEin Matrixwahrscheinlichkeitsproblem?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Quantilregression für probabilistische Zeitreihenprognosen
May 07, 2024 pm 05:04 PM
Quantilregression für probabilistische Zeitreihenprognosen
May 07, 2024 pm 05:04 PM
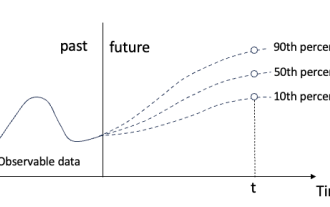
Ändern Sie nicht die Bedeutung des ursprünglichen Inhalts, optimieren Sie den Inhalt nicht, schreiben Sie den Inhalt neu und fahren Sie nicht fort. „Die Quantilregression erfüllt diesen Bedarf, indem sie Vorhersageintervalle mit quantifizierten Chancen bereitstellt. Dabei handelt es sich um eine statistische Technik zur Modellierung der Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen, insbesondere wenn die bedingte Verteilung der Antwortvariablen von Interesse ist. Im Gegensatz zur herkömmlichen Regression Methoden: Die Quantilregression konzentriert sich auf die Schätzung der bedingten Größe der Antwortvariablen und nicht auf den bedingten Mittelwert Quantile der erklärten Variablen Y. Das bestehende Regressionsmodell ist eigentlich eine Methode zur Untersuchung der Beziehung zwischen der erklärten Variablen und der erklärenden Variablen. Sie konzentrieren sich auf die Beziehung zwischen erklärenden Variablen und erklärten Variablen
 Erkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2)
Nov 20, 2023 pm 05:25 PM
Erkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2)
Nov 20, 2023 pm 05:25 PM
Im ersten Artikel dieser Reihe haben wir die Zusammenhänge und Unterschiede zwischen künstlicher Intelligenz, maschinellem Lernen, Deep Learning, Datenwissenschaft und mehr diskutiert. Wir haben auch einige schwierige Entscheidungen hinsichtlich der Programmiersprachen, Tools und mehr getroffen, die in der gesamten Serie verwendet werden sollen. Abschließend haben wir noch ein wenig Matrixwissen eingeführt. In diesem Artikel werden wir die Matrix, den Kern der künstlichen Intelligenz, ausführlich besprechen. Aber vorher wollen wir zunächst die Geschichte der künstlichen Intelligenz verstehen. Warum müssen wir die Geschichte der künstlichen Intelligenz verstehen? In der Geschichte gab es viele KI-Booms, aber in vielen Fällen blieben die großen Erwartungen an das Potenzial der KI aus. Das Verständnis der Geschichte der künstlichen Intelligenz kann uns helfen zu erkennen, ob diese Welle der künstlichen Intelligenz Wunder bewirken wird oder nur eine weitere Blase ist, die kurz vor dem Platzen steht. uns
 Probleme bei der Bewertung des Clustering-Effekts in Clustering-Algorithmen
Oct 10, 2023 pm 01:12 PM
Probleme bei der Bewertung des Clustering-Effekts in Clustering-Algorithmen
Oct 10, 2023 pm 01:12 PM
Das Problem der Clustering-Effektbewertung im Clustering-Algorithmus erfordert spezifische Codebeispiele. Clustering ist eine unbeaufsichtigte Lernmethode, die ähnliche Stichproben durch Clustering von Daten in eine Kategorie gruppiert. Bei Clustering-Algorithmen ist die Bewertung des Clustering-Effekts ein wichtiges Thema. In diesem Artikel werden mehrere häufig verwendete Indikatoren zur Bewertung des Clustering-Effekts vorgestellt und entsprechende Codebeispiele gegeben. 1. Clustering-Effekt-Bewertungsindex Silhouette-Koeffizient Der Silhouette-Koeffizient bewertet den Clustering-Effekt, indem er die Nähe der Stichprobe und den Grad der Trennung von anderen Clustern berechnet.
 Erfahren Sie, wie Sie häufige iPhone-Probleme diagnostizieren
Dec 03, 2023 am 08:15 AM
Erfahren Sie, wie Sie häufige iPhone-Probleme diagnostizieren
Dec 03, 2023 am 08:15 AM
Das iPhone ist für seine leistungsstarke Leistung und seine vielseitigen Funktionen bekannt und ist nicht immun gegen gelegentliche Probleme oder technische Schwierigkeiten, ein häufiges Merkmal komplexer elektronischer Geräte. iPhone-Probleme können frustrierend sein, aber normalerweise ist kein Alarm erforderlich. In diesem umfassenden Leitfaden möchten wir einige der am häufigsten auftretenden Herausforderungen im Zusammenhang mit der iPhone-Nutzung entmystifizieren. Unser Schritt-für-Schritt-Ansatz soll Ihnen bei der Lösung dieser häufigen Probleme helfen und praktische Lösungen und Tipps zur Fehlerbehebung bieten, damit Ihre Geräte wieder einwandfrei funktionieren. Unabhängig davon, ob Sie mit einer Störung oder einem komplexeren Problem konfrontiert sind, kann Ihnen dieser Artikel dabei helfen, diese effektiv zu beheben. Allgemeine Tipps zur Fehlerbehebung Bevor wir uns mit den spezifischen Schritten zur Fehlerbehebung befassen, finden Sie hier einige hilfreiche Tipps
 So lösen Sie das Problem, dass jQuery den Formularelementwert nicht abrufen kann
Feb 19, 2024 pm 02:01 PM
So lösen Sie das Problem, dass jQuery den Formularelementwert nicht abrufen kann
Feb 19, 2024 pm 02:01 PM
Um das Problem zu lösen, dass jQuery.val() nicht verwendet werden kann, sind spezifische Codebeispiele erforderlich. Für Front-End-Entwickler ist die Verwendung von jQuery eine der häufigsten Operationen. Unter diesen ist die Verwendung der .val()-Methode zum Abrufen oder Festlegen des Werts eines Formularelements eine sehr häufige Operation. In bestimmten Fällen kann jedoch das Problem auftreten, dass die Methode .val() nicht verwendet werden kann. In diesem Artikel werden einige gängige Situationen und Lösungen vorgestellt und spezifische Codebeispiele bereitgestellt. Problembeschreibung: Wenn Sie jQuery zum Entwickeln von Front-End-Seiten verwenden, treten manchmal Probleme auf
 Python-Programm zum Multiplizieren zweier Matrizen mithilfe mehrdimensionaler Arrays
Sep 11, 2023 pm 05:09 PM
Python-Programm zum Multiplizieren zweier Matrizen mithilfe mehrdimensionaler Arrays
Sep 11, 2023 pm 05:09 PM
Eine Matrix ist eine Menge von Zahlen, die in Zeilen und Spalten angeordnet sind. Eine Matrix mit m Zeilen und n Spalten wird als mXn-Matrix bezeichnet, und m und n werden als ihre Dimensionen bezeichnet. Eine Matrix ist ein zweidimensionales Array, das in Python mithilfe von Listen oder NumPy-Arrays erstellt wird. Im Allgemeinen kann die Matrixmultiplikation durch Multiplikation der Zeilen der ersten Matrix mit den Spalten der zweiten Matrix erfolgen. Dabei sollte die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix sein. Eingabe- und Ausgabeszenario Angenommen, wir haben zwei Matrizen A und B. Die Abmessungen dieser beiden Matrizen betragen 2X3 bzw. 3X2. Die resultierende Matrix nach der Multiplikation hat 2 Zeilen und 1 Spalte. [b1,b2][a1,a2,a3]*[b3,b4]=[a1*b1+a2*b2+a3*a3][a4,a5,a6][b5,b6][a4*b2+a
 Das Problem der Generalisierungsfähigkeit maschineller Lernmodelle
Oct 08, 2023 am 10:46 AM
Das Problem der Generalisierungsfähigkeit maschineller Lernmodelle
Oct 08, 2023 am 10:46 AM
Die Generalisierungsfähigkeit von Modellen für maschinelles Lernen erfordert spezifische Codebeispiele. Da die Entwicklung und Anwendung von maschinellem Lernen immer weiter verbreitet wird, wird der Generalisierungsfähigkeit von Modellen für maschinelles Lernen immer mehr Aufmerksamkeit geschenkt. Die Generalisierungsfähigkeit bezieht sich auf die Vorhersagefähigkeit eines maschinellen Lernmodells anhand unbeschrifteter Daten und kann auch als Anpassungsfähigkeit des Modells in der realen Welt verstanden werden. Ein gutes Modell für maschinelles Lernen sollte über eine hohe Generalisierungsfähigkeit verfügen und in der Lage sein, genaue Vorhersagen für neue Daten zu treffen. In praktischen Anwendungen stoßen wir jedoch häufig auf Modelle, die im Trainingssatz gut funktionieren, im Testsatz oder in der Realität jedoch versagen
 Problem beim Erwerb von Etiketten beim schwach überwachten Lernen
Oct 08, 2023 am 09:18 AM
Problem beim Erwerb von Etiketten beim schwach überwachten Lernen
Oct 08, 2023 am 09:18 AM
Das Problem der Etikettenerfassung beim schwach überwachten Lernen erfordert spezifische Codebeispiele. Einführung: Schwach überwachtes Lernen ist eine Methode des maschinellen Lernens, die schwache Etiketten für das Training verwendet. Im Gegensatz zum herkömmlichen überwachten Lernen müssen beim schwach überwachten Lernen nur weniger Beschriftungen zum Trainieren des Modells verwendet werden, und nicht jede Probe muss über eine genaue Beschriftung verfügen. Beim schwach überwachten Lernen ist jedoch die Frage, wie aus schwachen Labels nützliche Informationen genau gewonnen werden können, ein zentrales Thema. In diesem Artikel wird das Problem der Etikettenerfassung beim schwach überwachten Lernen vorgestellt und spezifische Codebeispiele gegeben. Einführung in das Label-Akquisitionsproblem beim schwach überwachten Lernen:




