C/C++-Programm zur Berechnung der Anzahl der nachgestellten Nullen in der Fakultät einer Zahl

Hier erfahren Sie, wie Sie die Anzahl der nachgestellten Nullen im faktoriellen Ergebnis einer beliebigen Zahl berechnen. Wenn also n = 5, dann 5! =120. Es gibt nur eine abschließende 0. Für 20! wären es 4 Nullen als 20! = 2432902008176640000.

Am einfachsten ist es, die Fakultät zu berechnen und 0 zu berechnen. Aber für größere Werte von n schlägt dieser Ansatz fehl. Deshalb werden wir einen anderen Ansatz wählen. Wenn die Primfaktoren 2 und 5 sind, erscheinen nachgestellte Nullen. Wenn wir 2 und 5 berechnen, erhalten wir das Ergebnis. Dazu befolgen wir diese Regel.

TrailingZeros(n) = Zählen von 5 in faktoriellen (n) Primfaktoren

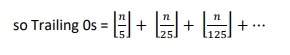
Algorithmus

countTrailingZeros(n)

begin
   count := 0
   for i := 5, (n/i) >= 1, increase i := i * 5, do
      count := count + (n / i)
   done
   return count;
end

Beispiel

Die chinesische Übersetzung lautet:

Beispiel

#include <iostream>
#include <cmath>
#define MAX 20
using namespace std;
int countTrailingZeros(int n) {
   int count = 0;
   for (int i = 5; n / i >= 1; i *= 5)
      count += n / i;
   return count;
}
main() {
   int n = 20;
   cout << "Number of trailing zeros: " << countTrailingZeros(n);
}

Ausgabe

Number of trailing zeros: 4

Das obige ist der detaillierte Inhalt vonC/C++-Programm zur Berechnung der Anzahl der nachgestellten Nullen in der Fakultät einer Zahl. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!