 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 Was ist das größte Reuleaux-Dreieck innerhalb eines Quadrats, das in eine Ellipse eingeschrieben ist?
Was ist das größte Reuleaux-Dreieck innerhalb eines Quadrats, das in eine Ellipse eingeschrieben ist?
Was ist das größte Reuleaux-Dreieck innerhalb eines Quadrats, das in eine Ellipse eingeschrieben ist?
Hier sehen wir die Fläche eines größten Ruhrdreiecks, das in ein Quadrat eingeschrieben ist, das in eine Ellipse eingeschrieben ist. Wir wissen, dass die Länge der Hauptachse der Ellipse 2a und die Länge der Nebenachse 2b beträgt. Die Seitenlänge des Quadrats beträgt „x“ und die Höhe des Luer-Dreiecks beträgt h.
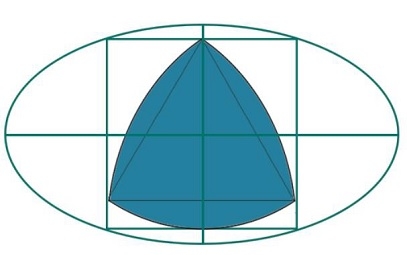
Wir wissen, dass die Seitenlänge des in die Ellipse mit der Hauptachse 2a und der Nebenachse 2b eingeschriebenen Quadrats −
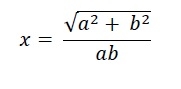
beträgt. Die Höhe des Ruhrdreiecks ist gleich a. Also h = x. Daher beträgt die Fläche des Ruhrdreiecks −
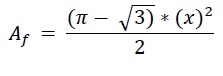 .
.
Beispiel
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float a, float b) { //a and b are half of major and minor axis of ellipse
if (a < 0 || b < 0) //either a or b is negative it is invalid
return -1;
float x = sqrt((a*a) + (b*b)) / (a*b);
float area = ((3.1415 - sqrt(3)) * (x) * (x))/2;
return area;
}
int main() {
float a = 5;
float b = 4;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(a, b);
}Ausgabe
Area of Reuleaux Triangle: 0.0722343
Das obige ist der detaillierte Inhalt vonWas ist das größte Reuleaux-Dreieck innerhalb eines Quadrats, das in eine Ellipse eingeschrieben ist?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1659
1659
 14
14
 1416
1416
 52
52
 1310
1310
 25
25
 1259
1259
 29
29
 1233
1233
 24
24
 Finden Sie die Fläche eines Kreises, der in ein Quadrat in Java eingeschrieben ist
Aug 19, 2023 pm 04:53 PM
Finden Sie die Fläche eines Kreises, der in ein Quadrat in Java eingeschrieben ist
Aug 19, 2023 pm 04:53 PM
Ein Kreis ist ein zweidimensionales Diagramm, das keine Ecken hat. Jeder Kreis hat einen Ursprungspunkt, und jeder Punkt auf dem Kreis hat den gleichen Abstand vom Ursprung. Der Abstand zwischen dem Ursprung und dem Punkt eines Kreises wird als Radius des Kreises bezeichnet
 Was ist das größte Quadrat, das in ein gleichseitiges Dreieck eingeschrieben werden kann?
Sep 22, 2023 pm 06:21 PM
Was ist das größte Quadrat, das in ein gleichseitiges Dreieck eingeschrieben werden kann?
Sep 22, 2023 pm 06:21 PM
Hier sehen wir die Fläche des größten Quadrats, das in ein gleichseitiges Dreieck eingeschrieben werden kann. Die Seitenlänge des Dreiecks ist „a“ und die Seitenlänge des Quadrats ist x. Die Seitenlänge „a“ des Dreiecks beträgt − also ist x − Beispiel #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
 Übersetzen Sie in einem C-Programm Folgendes ins Chinesische: Wie groß ist die Fläche eines Quadrats, das in einen Kreis eingeschrieben ist, der in ein gleichseitiges Dreieck eingeschrieben ist?
Aug 31, 2023 pm 12:25 PM
Übersetzen Sie in einem C-Programm Folgendes ins Chinesische: Wie groß ist die Fläche eines Quadrats, das in einen Kreis eingeschrieben ist, der in ein gleichseitiges Dreieck eingeschrieben ist?
Aug 31, 2023 pm 12:25 PM
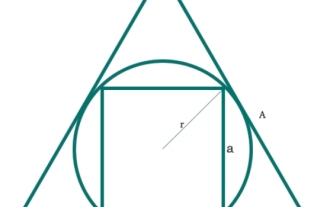
Hier sehen wir, dass die Fläche eines Quadrats in einen Kreis eingeschrieben ist und dass der Kreis in ein gleichseitiges Dreieck eingeschrieben ist. Die Seite des Quadrats ist „a“. Der Radius des Kreises ist „r“ und die Seite des Sechsecks ist „A“. Das Diagramm ist unten dargestellt. Die Diagonale des Quadrats ist also – also die Fläche des Quadrats – Beispiel #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne
 Was ist das größte Ruero-Dreieck, das in ein Quadrat eingeschrieben ist, das ein rechtwinkliges Dreieck ist?
Sep 04, 2023 pm 10:29 PM
Was ist das größte Ruero-Dreieck, das in ein Quadrat eingeschrieben ist, das ein rechtwinkliges Dreieck ist?
Sep 04, 2023 pm 10:29 PM
Hier sehen wir die Fläche des größten Reuleaux-Dreiecks, eingeschrieben in ein Quadrat, das wiederum in ein rechtwinkliges Dreieck eingeschrieben ist. Die Seitenlänge des Quadrats ist „a“. Die Höhe eines Reuleaux-Dreiecks beträgt x. Die Basis des Dreiecks ist b, die Höhe ist l und die Hypotenuse ist h. Wir wissen, dass ein Quadrat, das in ein rechtwinkliges Dreieck mit der Höhe l und der Grundfläche b eingeschrieben ist, eine Seitenlänge hat – die Höhe eines Reuleaux-Dreiecks ist gleich a. Also a=x. Daher beträgt die Fläche eines Reuleaux-Dreiecks – Beispiel#include<iostream>#include<cmath>usingnamespacestd;fl
 In C das größte Reuleaux-Dreieck innerhalb eines Quadrats
Sep 07, 2023 pm 12:29 PM
In C das größte Reuleaux-Dreieck innerhalb eines Quadrats
Sep 07, 2023 pm 12:29 PM
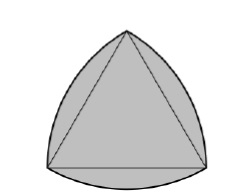
Ein Lule-Dreieck ist eine Form, die durch den Schnittpunkt von drei Scheiben entsteht, wobei der Mittelpunkt jeder Scheibe auf der Grenze der anderen beiden Scheiben liegt. Sein Rand ist eine Kurve konstanter Breite und neben dem Kreis selbst die einfachste und bekannteste Kurve dieser Art. Konstante Breite bedeutet, dass der Abstand zwischen jeweils zwei parallelen Stützlinien unabhängig von ihrer Ausrichtung gleich ist. Weil alle Durchmesser gleich sind. Die Grenzen des Lule-Dreiecks sind Kurven konstanter Breite, die auf gleichseitigen Dreiecken basieren. Alle Punkte einer Kante haben den gleichen Abstand vom gegenüberliegenden Scheitelpunkt. Die Formel zum Konstruieren eines Lule-Dreiecks. Wenn die Kurve auf einem gleichseitigen Dreieck basiert und die Seitenlänge des Dreiecks h ist, dann ist die Fläche des Lule-Dreiecks A=(π*h2)/2–2*( Areao
 C-Programm zur Berechnung der Fläche eines Quadrats innerhalb eines Kreises, der in ein Sechseck eingeschrieben ist
Aug 28, 2023 pm 08:41 PM
C-Programm zur Berechnung der Fläche eines Quadrats innerhalb eines Kreises, der in ein Sechseck eingeschrieben ist
Aug 28, 2023 pm 08:41 PM
Gegeben sei ein Quadrat, das in einen Kreis eingeschrieben ist, der von einem regelmäßigen Sechseck umschrieben ist. Wir müssen die Fläche des Quadrats ermitteln und dazu müssen wir die Beziehung zwischen den Seitenlängen des Quadrats und den Seitenlängen des regelmäßigen Sechsecks ermitteln . Die mathematische Formel für den Radius des eingeschriebenen Kreises eines regelmäßigen Sechsecks lautet: r=A√3/2 Da die Diagonale des Quadrats gleich dem Durchmesser des Kreises ist, lautet die Beziehung zwischen dem Radius und der Seitenlänge: a=√r gemäß dem regulären Sechseck. Die Seitenlänge von a=√3A/√2, also die Fläche des Quadrats, area=a2=(√3A/√2)2 Beispiel #include<stdio. h>#inclu
 Berechnen Sie die Fläche der Blätter innerhalb eines Quadrats im C-Programm
Sep 24, 2023 pm 09:13 PM
Berechnen Sie die Fläche der Blätter innerhalb eines Quadrats im C-Programm
Sep 24, 2023 pm 09:13 PM
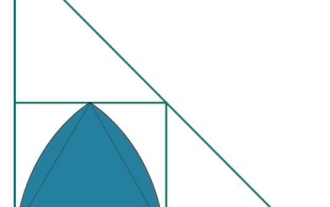
Um die Fläche eines Blattes innerhalb eines Quadrats zu ermitteln, müssen wir es in Teile teilen und die Fläche jedes Teils ermitteln. Anschließend müssen wir diese Flächen addieren, um die Fläche des Blattes zu ermitteln. Um die Fläche zu berechnen, müssen wir das Blatt in zwei Teile teilen. Um die Fläche des ersten Teils AECA zu ermitteln, ermitteln wir die Fläche des Vierecks AECDA und subtrahieren davon die Fläche des Dreiecks ACDA. Quadrantenfläche=1⁄4*(π*r2)wobei π=22/7 oder 3,141. Die Fläche eines rechtwinkligen Dreiecks=1⁄2*B*H=½a2Beispiel #include#definePI3.14159265intmain(){ floata=12.3;
 Wie groß ist die Fläche eines Blattes innerhalb eines Quadrats?
Aug 26, 2023 pm 05:13 PM
Wie groß ist die Fläche eines Blattes innerhalb eines Quadrats?
Aug 26, 2023 pm 05:13 PM
Hier sehen wir, wie man die Fläche eines blattähnlichen Objekts berechnet, das innerhalb eines Quadrats ABCD liegt. Jede Seite des Quadrats hat die Länge „a“. Das Blatt besteht aus zwei gleichen Teilen. Die Fläche jedes Teils beträgt p, jetzt beträgt die Fläche des gesamten Blattes 2p. Beispiel #include<iostream>usingnamespacestd;floatleafArea(floata){ return(a*a*(3.1415/2-1));}intmain(){ floatsquare



